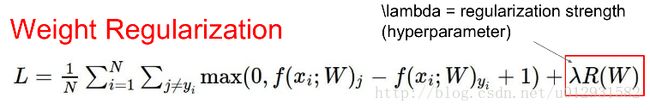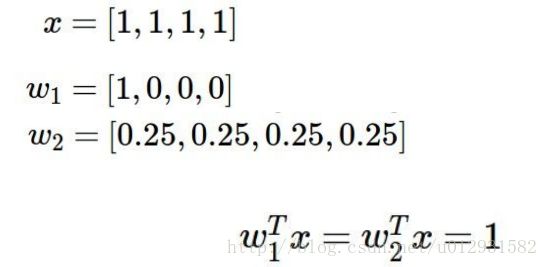cs231n-svm和softmax
cs231n-svm和softmax
- cs231n-svm和softmax
- 回顾
- 损失函数
- svm损失函数
- 权值矩阵初始化
- 正则化
- Softmax 损失函数
- svm vs softmax
- svm损失函数
- 总结线性分类器svm softmax
回顾
上一篇我们讲到了线性分类器以及在图像分类当中的应用,其中得分函数是:
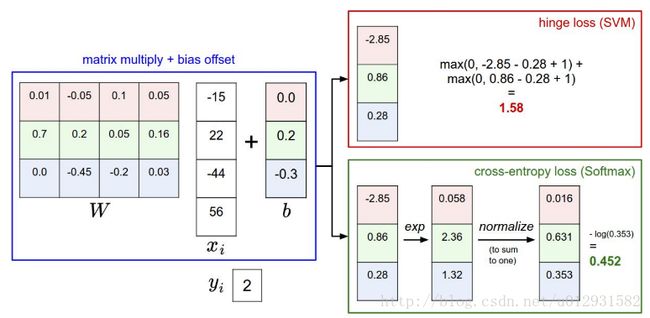
输入图像x,通过权值矩阵加上偏置得到最后的分数,其中分数最高的类别就是最后的结果,过程如下图所示:
下面就讲一下权值矩阵的产生和训练过程
损失函数
损失函数是用来评价当前得分的好坏,又称为代价函数或者目标函数,如果结果越好,那么损失函数将越低.
svm损失函数
这里定义SVM的loss函数。SVM loss会使正确类别的得分比错误类别的得分至少高Δ。用s代表分数，第i个图像对应第j类的得分 sj=f(xi,W)j ，那么多类别SVM对于第i个图像的loss为
Li=∑j≠yimax(0,sj−syi+Δ))
因为用的是线性分类器,也就是说得分函数是线性函数,所以也可以写作:
Li=∑j≠yimax(0,wTjxi−wTyixi+Δ))
在实际应用过程中,Δ一般取1. Δ到底有什么作用接下来再说.
上面的损失函数也叫作hinge loss,形式就是 max(0,−)
下图就是多类别SVM loss可视化图。
举个例子,现在又三幅图片,计算各自的损失函数,总的损失函数就是取均值:
L=1N∑Ni=1Li
权值矩阵初始化
一开始W是给定非常小的随机数,所以 s =0 ,那么这个时候损失函数的值就是Δ,如果Δ为0,那么损失函数一开始就是0,达到最小,也就不会进行接下来的优化了,这就解答了上面提到的Δ必须的问题.
正则化
目前得到的损失函数如下:
L=1N∑Ni=1∑j≠yimax(0,wTjxi−wTyixi+Δ))
但是有一个问题,那就是最优解不唯一,比如说 W=W1 的时候L=0,那么很显然 W=2∗W1 的时候L也为0,所以我们需要加上一个正则项 λR(W) :
最常用的正则项都是用的L2范式:
加了正则项之后,有两个效果:
1. W就趋向于0,但是由于Δ的存在,W最后又不可能变成0
2. W会趋于均匀分布,如下例所示
可以看出两个权值矩阵最后得到的损失相同,但是由于正则项的存在,权值分布更加均匀的 W2 最后的损失更小,所以最后权值矩阵更加像 W2 .
Softmax 损失函数
首先Softmax函数的定义如下: fj(z)=ezj∑kezk
将图片 xi 分为k类的归一化概率如下: P(Y=k|X=xi)=ezj∑kezk , 其中 s=f(xi;W)
损失函数取负对数如下:
Li=−logP(Y=yi|X=xi)
可知,该损失函数最小为0,最大为无穷.当权值矩阵初始化为随机的非常小的数时,s~=0,那么 Li =log(N) ,其中N为类别数.
svm vs softmax
举一个例子进行对比:
SVM计算每类的得分，这样不易直接解释。Softmax计算每类的概率。超参数λ控制概率的集中或离散程度。
实践中，SVM和Softmax常常是相似的：SVM和Softmax性能差别不大，不同的人对哪种效果更好持不同的观点。和Softmax相比，SVM更加局部化（local objective），它只关心小于间隔Δ的部分，例如Δ=1，那么分值[10, -100, -100]和[10, 9, 9]对于SVM来说，其loss函数值相同；但是对于softmax就不同了。Softmax的loss函数只有在完全正确情况下才会为0。
总结线性分类器(svm && softmax)
1、定义了评价函数，线性函数的评价函数依赖权重W和偏置b。
2、和kNN使用不一样，参数化方法训练时间比较久，预测只是矩阵相乘。
3、通过一个trick，可以把偏置加入到矩阵相乘中。
4、定义了loss 函数，介绍了常用的SVM和Softmax loss。对比了两者的区别。
对应的课程作业可以参考我的下一篇文章.
接下来就讲一下梯度下降,以及如何应用到svm和softmax中并且进行图像的分类.