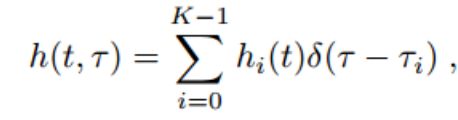【文献学习】 2021 Deep-Waveform: A Learned OFDM Receiver Based on Deep Complex Convolutional Networks

2018版 https://arxiv.org/abs/1810.07181
2018译文
参考文章
参考文章

深波：一种基于深复卷积网络的学习OFDM接收机：

V 结果评估
OFDM系统和衰落信道配置如表III所示，采样率为10Mbps。一个OFDM帧包含8个OFDM符号，FFT大小为64，循环前缀（CP）长度为16。每个OFDM符号有10个保护子载波（SCs），包括直流（DC）、8个导频SCs和46个数据SCs。每帧中的导频和数据单元的数目分别为64和368。如图8所示，飞行员分散分布在所有非防护SCs上。这种导频模式在频谱资源方面是有效的，并确保基准信道估计算法的一致性能，与其他类型的导频模式相同[8]。每个导频的值为1+1i。给定调制下星座的最大功率被归一化为导频功率。采用灰色编码实现星座与位之间的映射。发射后，OFDM波形的峰均功率比（PAPR）被限制在9dB。对AWGN和Rayleigh信道进行了测试。衰落信道包括平坦衰落和多径衰落，后者是3GPP[30]提出的扩展行人A模型（EPA）。考虑慢衰落，信道抽头每帧更新一次。在EPA模型下，帧内存在码间干扰（ISI），而帧间没有码间干扰，可以通过帧间的缝隙来消除。EPA模型（450ns）的延迟扩展比CP（1600ns）短。为了简单起见，在接收机处考虑了完全同步，因此忽略了时间和频率偏移以及多普勒频移，这在[2]，[6]中已经讨论过。该配置模拟了LTE系统的基线场景。对于衰落信道，根据64个OFDM帧（512个OFDM符号）的平均信号功率，根据SNR设置噪声功率。
————————————————
版权声明：本文为CSDN博主「Better Bench」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_43935696/article/details/107988405

2018版代码见本地
代码2
2021版代码 https://codechina.csdn.net/mirrors/zhongyuanzhao/dl_ofdm?utm_source=csdn_github_accelerator

---

被引文：

• DeepRx: Fully Convolutional Deep Learning Receive
• A novel OFDM autoencoder featuring CNN-based channel estimation for Internet of vessels （lov物联网，2020 ） 引用16次
• 原代码
  个人仓
• Deep neural network-based underwater OFDM receiver

---

创新点：
1、CNN被应用于实现直接从时域RX信号中提取比特估计的接收机，在低到中信噪比时获得了优异的性能。
2、对复数信号直接处理，避免了实部虚部分开处理带来的不可预知的幅度相位损失

---

缩写
自动编码器(AE)
complex-valued neural networks (CVNNs)复数卷积神经网络
物理层(PHY)
多层感知器(MLP) 即dnn
power-delay profile (PDP)
什么是低phy？

[1] T. Wang, C. Wen, H. Wang, F. Gao, T. Jiang, and S. Jin, “Deep learning for wireless physical layer: Opportunities and challenges,” China Communications, vol. 14, no. 11, pp. 92–111, Nov 2017.
[2] Q. Mao, F. Hu, and Q. Hao, “Deep learning for intelligent wireless networks: A comprehensive survey,” IEEE Communications Surveys
Tutorials, pp. 1–1, 2018.
[3] D. G¨und¨uz, P. de Kerret, N. D. Sidiropoulos, D. Gesbert, C. R. Murthy,
and M. van der Schaar, “Machine learning in the air,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 10, pp. 2184–2199,2019

Abstract

—（逆）离散傅里叶变换（DFT/IDFT）通常被认为是正交频分复用(OFDM)系统的关键部分。本文开发了一种深度复值卷积网络(DCCN)，在不依赖任何显式DFT/IDFT的情况下从时域OFDM信号中恢复比特。DCCN可以用学习的线性变换代替DFT，利用OFDM波形的循环前缀(CP)来提高信噪比，并具有利用CP、信道估计和信间干扰(ISI)缓解的优点，复杂度为O(N2)。数值测试表明，基于理想和具有不同延迟扩散和迁移率的线性最小均方误差(LMMSE)估计和传统的瑞利衰落信道，DCCN接收机的性能优于传统的信道估计器。所提出的方法得益于复杂值神经网络的表达性质，然而，它目前缺乏来自流行的深度学习平台的支持。
为此，为无线PHY卷积网络的设计和分析提供了复杂值卷积层精确和近似实现的准则。为了提高训练模型在衰落信道中的收敛性和通用性，提出了一套新的训练技术。本工作证明了深层神经网络处理OFDM波形的能力，结果表明，在OFDM接收机中，FFT处理器可以用硬件AI加速器代替。

I. INTRODUCTION

近年来，无线通信物理层(PHY)的深度学习研究了各种任务[1]–[3]，，包括信号分类[4]，[5]，参数估计、[5]–[9]，参数估计、信道估计[8]–[20]，信道编码[16]，[21]，[22]，检测[11]，[16]，[23]–[26]，调制星座[7]的设计和导频设计[27]，[28]。
深度神经网络(DNNs)不仅可以增强无线PHY的某些功能和组件，还可以开发为一种端到端新的通信架构，被视为自动编码器(AE)[6]-[8]、[17]、[21]、[22]。

6.T. O’Shea and J. Hoydis, “An introduction to deep learning for the physical layer”, IEEE Trans. Cognit. Commun. Netw., vol. 3, no. 4, pp. 563-575, Dec. 2017. 7次
7.S. Dorner, S. Cammerer, J. Hoydis and S. ten Brink, “On deep learning-based communication over the air”, Proc. 51st Asilomar Conf. Signals Syst. Comput., pp. 1791-1795, Oct. 2017. 9次
8.A. Felix, S. Cammerer, S. Dorner, J. Hoydis and S. Ten Brink, “OFDM-autoencoder for end-to-end learning of communications systems”, Proc. IEEE 19th Int. Workshop Signal Process. Adv. Wireless Commun. (SPAWC), pp. 1-5, Jun. 2018. 8次
17.B. Lin, X. Wang, W. Yuan and N. Wu, “A novel OFDM autoencoder featuring CNN-based channel estimation for Internet of vessels”, IEEE Internet Things J., vol. 7, no. 8, pp. 7601-7611, Aug. 2020. 引用五次
21.T. J. O’Shea, K. Karra and T. C. Clancy, “Learning to communicate: Channel auto-encoders domain specific regularizers and attention”, Proc. IEEE Int. Symp. Signal Process. Inf. Technol. (ISSPIT), pp. 223-228, Dec. 2016. 引用6次
22.T. J. O’Shea, T. Erpek and T. Charles Clancy, “Deep learning based MIMO communications” in arXiv:1707.07980, 2017, [online] Available: http://arxiv.org/abs/1707.07980. 引用6次

一个通信AE(图1的底部)不是像图像和文本数据(如图1的顶部）寻求一个紧凑的嵌入结构化数据，而是生成非结构化比特的冗余表示，在被有噪声的通道污染后，可以从中恢复原始信息。通信AE通过自监督学习一组随机比特作为训练数据，通过数据的结构来学习信道的行为。在PHY之上，深度学习也用于资源分配和网络管理，如流量预测[29]、干扰对齐[30]、功率控制[31]、频谱共享[32]和调度[33]。

与DL领域典型的处理图像、自然语言等结构化数据的AE相比，通信AE具有两个独特的特点，如图1所示。第一，通信AE的目标是寻找能够在不利的无线信道上携带信息的隐藏编码，一般是通过增加冗余度来实现，而典型AE的目的是在低维的潜伏空间中寻找结构化数据的紧凑表示，而不担心编码的污染。其次，通信AE的目的是学习信道的继承行为，而不是数据的结构。通信AE中的数据–输入和输出位–被认为是非结构化和不可压缩的。因此，通信AE应该在一组随机数据的通道上进行训练。
————————————————

数据驱动的深度学习方法提供了无线PHY的几个优点：
(1)结合信号处理链中的级联模块实现协同效应[6]，[7]，
II)减少底层模型与现实之间的不匹配，
(3)利用DNN[11]，[16]，[25]，[26]的非线性来构造低复杂度的解决方案
(4)发现不规则和/或自适应的设计，例如用于试验设计[27]，[28]和调制星座[6]，[7]。

解释为什么用CVNNs
与图像或文本解释相比，无线通信的一个主要区别是依赖复杂领域无线信号的表示。然而，目前流行的TensorFlow [36] 、Keras[37]等无线PHY深度学习平台并不支持 complex-valued neural networks (CVNNs)复数卷积神经网络(CVNNs)[34]，[35] ，这是机器学习学科的一个新兴领域。相反，现有的研究分别处理复值张量的实部和虚部，C⇒R2，如约D：两个平行实值张量[7]、[11]、[16]或约C：实值张量[28]的两个通道。然而，在乘法操作中，C（复数）不同于R（实数）空间，如果没有说明，会阻碍DNN充分利用信号样本的实部和振幅之间的关系，从而增加复杂性、降低性能并且限制其可解释性。

[34] A. Hirose, Complex-valued neural networks. Springer Science &
Business Media, 2012, vol. 400.
[35] C. Trabelsi, O. Bilaniuk, Y. Zhang, D. Serdyuk, S. Subramanian,
J. F. Santos, S. Mehri, N. Rostamzadeh, Y. Bengio, and C. J. Pal,
“Deep complex networks,” in International Conference on Learning
Representations (ICLR), 2018

没懂
For example, orthogonal frequency-division multiplexing (OFDM) systems require (inverse) discrete Fourier transform (DFT/IDFT) and/or linear finite impulse-response (FIR) filters that are defined in the complex field C. Without complex-valued representation , existing deep learning-based OFDM receivers[8], [10], [11], [13]–[14][15][16], [23] and AE [8] are limited to relying on DFT/IDFT in processing the OFDM waveform. Regarding technical solutions, convolutional neural networks (CNNs) [4], [5], [16], [23], [24], [28] are less often used than multilayer perceptron (MLP) [6]–[7][8][9][10][11][12], [21], [22], [25] in wireless PHY despite their higher efficiency, as CNN depends on the assumptions of the underlying process and is harder to design for the operations in the complex field.

例如，正交频分多路复用（OFDM)系统需要的 (逆)离散傅里叶变换（DFT/IDFT）和/或线性有限脉冲响应(FIR)滤波器，它们都是在复数空间中定义。在没有复数表示的情况下，现有的基于深度学习的OFDM接收器[8]、[10]、[11]、[13]-[16]、[23]和AE[8]只能在处理OFDM波形时依赖于DFT/IDFT。
关于技术解决方案，卷积神经网络(CNNs) [4]、[5]、[16]、[23]、[24]、[28] 比多层感知器(MLP) [6]-[7][8] [9][10][11][12]、[21]、[22]、[25]在无线PHY中的使用要少，因为CNN依赖于基础过程的假设，更难设计复杂领域的操作。因为CNN虽然效率更高，但是依赖于底层过程的假设，并且更难为复数域的操作进行设计。

[8] A. Felix, S. Cammerer, S. D¨orner, J. Hoydis, and S. ten Brink, “OFDM autoencoder for end-to-end learning of communications systems,” 2018
IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), pp. 1–5, 2018.
[10] C.-H. Cheng, Y.-H. Huang, and H.-C. Chen, “Channel estimation in
OFDM systems using neural network technology combined with a
genetic algorithm,” Soft Computing, vol. 20, no. 10, pp. 4139–4148,2016.
[11] H. Ye, G. Y. Li, and B. Juang, “Power of deep learning for channel
estimation and signal detection in OFDM systems,” IEEE Wireless
Communications Letters, vol. 7, no. 1, pp. 114–117, Feb 2018.

---

在本文中，我们提出了一种深度复值卷积网络(DCCN)设计来从同步时域OFDM信号中恢复比特。开发的端到端OFDM接收器不依赖DFT/IDFT，而是学习了一种接收改进的信噪比(SNR)的OFDM波形，这证明了OFDM波形深度学习的潜力。通过利用CVNNs环境中的最新发展，DCCN接收器的性能优于瑞利衰落信道中的传统接收器。此外，基于域知识和OFDM框架结构，选择了DCCN的许多结构和维数超参数，为其他波形结构提供了一个可转移的设计模板。

DCCN接收器包含一个基本的OFDM接收器和一个分离的信道均衡器。遵循信号处理的原理，所开发的DCCN模型与现有的作品[4]、[6]、[8]仅使用线性修正单元(Relu)激活的全连接隐藏层有很大不同。我们的模型包含了稠密层和卷积层，而卷积层大多是线性激活的，同时还包含了residual connections 和 skip connections的新结构。此外，复数卷积层是在Tensorflow[16]内实现的，用于处理复数的IQ数据，而不是将其作为两个独立的实数处理。在AWGN信道中，基于DCCN的OFDM接收机在== 2,4,8和16 QAMs==上实现了与专家接收机相似的误码率(BER)，并且学会了利用循环前缀，在中低信噪比的Rayleigh信道中优于使用事先信道信息的LMMSE信道估计器。这项工作显示了深度学习在复数信号变换中的能力，而这是主波形和信道行为的关键。
————————————————

本文的其余部分组织如下：相关的工作在第二节中被讨论。第三节概述了OFDM系统和信道估计方法。第四节介绍了DCCN接收机的设计和培训方法。最后，在第六节中讨论了结论和未来的方向。

II. RELATED WORK

A.无线通信的深度神经网络

MLP对底层进程不作任何假设，用于信道估计[9]–[12]，[19]，检测[25]，[26]，和通信AE[6]–[8]，[21]，[22]。在这些研究中，MLP通常有3到5层，并且在信号路径中遵循两种配置。第一配置是通过：在接收机（发射机）处，MLP获取接收数据和导频（输入位），并输出估计传输符号或软位[7]、[8]、[11]、[25]、[26]（传输IQ样本[6]-[8]、[22]）。AE[6]-[8]、[22]中可能包含用来同步的其他组件。第二配置是估计器：MLP仅利用接收的导频或信号估计信道[9]、[10]、[12]、[19]或其他参数[7]、[9]，信号与传统系统单独恢复。在本文中, 所开发的DCCN采用4层MLP，在卷积层之间配置估计器进行信道估计.

CNN用于信号分类[4]和恢复[5]、信道估计[16]-[18]、[20]、[28]、[44]、[45]和检测[16]、[24]。虽然CNNs的性能可能不会超过MLP[21]，但它更有效率和可扩展性。例如，[16]中的OFDM接收器基于残差结构中深度可分离卷积级联与线性复杂度与线性最小均方误差(LMMSE)估计量相匹配。CNN也被配置为信号路径中的通过[16]、[24]和估计器[44]。其他类型的DNN，如广义回归神经网络(GRNN)[12]和长期短期记忆(LSTM)[14]，[17]也用于信道估计，而基于模型的DNN展开了一个迭代算法[23]用于检测。

[14] Y. Liao, Y. Hua, X. Dai, H. Yao, and X. Yang, “ChanEstNet: A deep learning based channel estimation for high-speed scenarios,” in ICC 2019 - 2019 IEEE International Conference on Communications (ICC),2019, pp. 1–6.
[16] M. Honkala, D. Korpi, and J. M. J. Huttunen, “DeepRx: Fully convolutional deep learning receiver,” IEEE Transactions on Wireless Communications, pp. 1–1, 2021.
23. H. He, C.-K. Wen, S. Jin and G. Y. Li, “A model-driven deep learning network for MIMO detection”, Proc. IEEE Global Conf. Signal Inf. Process. (GlobalSIP), pp. 584-588, Nov. 2018.

CVNN在[34]，[35]中讨论，但流行平台[36]，[37]中不支持它们。[35页，第1页]指出，CVNNs“由于没有积木而被边缘化”。在无线PHY中，大多数CNNs都是实数[4]、[16]、[18]、[20]、[24]、[28]、[45]，除了在[5]中使用单层复值卷积来实现振幅相位表示，这在许多应用中需要额外的相位(un)包装。根据第IV-A节的分析，CVNN的表达性质可以由MLP和CNN[16]，[28]来保存，并具有适当的输入格式和尺寸，例如，接收字段和滤波器的数量。 However, the lack of discussions on such settings makes it difficult to scale up the successful design of CNNs [16], [28] with respect to the system parameters including antenna number and DFT size, or transfer these experiences for future work.
然而，由于缺乏对这些设置的讨论，很难扩大CNNs[16][28]在系统参数(包括天线数目和DFT大小)方面的成功设计，也难以将这些经验传递给今后的工作。在这项工作中，提供了实现复值卷积层的指南，并将CVNN用于整个IQ领域。

[34] A. Hirose, Complex-valued neural networks. Springer Science &
Business Media, 2012, vol. 400.
[35] C. Trabelsi, O. Bilaniuk, Y. Zhang, D. Serdyuk, S. Subramanian,
J. F. Santos, S. Mehri, N. Rostamzadeh, Y. Bengio, and C. J. Pal,
“Deep complex networks,” in International Conference on Learning
Representations (ICLR), 2018.
[16] M. Honkala, D. Korpi, and J. M. J. Huttunen, “DeepRx: Fully convolutional deep learning receiver,” IEEE Transactions on Wireless Communications, pp. 1–1, 2021.
[28] M. B. Mashhadi and D. Gunduz, “Pruning the pilots: Deep learningbased pilot design and channel estimation for MIMO-OFDM systems,”2020.

B. OFDM系统和增强型信道估计

OFDM是现代无线网络中最流行的系统。在[46]、[47]中，引入了OFDM物理层和各种信道估计方法。

• 在发射机端，为了实现5G等下一代通信系统，几种增强的波形被引入到OFDM家族，如滤波器组多载波(FBMC)、UFMC、GFDM[48]。 这些改进的OFDM波形在各种干扰方面通常具有更好的特征。提出了一种基于星座增强方法[49]和深度学习(DL)的编码系统[13]来降低OFDM波形的峰值到平均功率比(PAPR)。基于MLP的FBMC信道估计器在高移动性信道[50]中显示出良好的性能。
• 大部分的改进都发生在接收机端。作为OFDM波形的部分复制，引入了循环前缀(CP)用于接收器处的同步和ISI缓解，如图2(b)所示。CP已经被用来通过提高信噪比、频率选择性和减轻干扰的[41]来增强盲的[39]-[42]和导频辅助的[38]信道估计。在[38]中，以前的OFDM符号的解码数据被用来恢复下一个符号的CP。然而，[38]中的该方法只能增强LS信道的估计。我们的模型通过在没有显式算法的情况下同时处理多个OFDM符号和更好的效率来完成了这一任务，该算法作为现有分析方法的补充，如最大似然[39]、[41]和因子图[40]、[42]对CP的利用。
  DNN也被用于增强OFDM接收器。在[11]中，5层MLP用于信道估计和符号检测。

[11] H. Ye, G. Y. Li, and B. Juang, “Power of deep learning for channel estimation and signal detection in OFDM systems,” IEEE Wireless Communications Letters, vol. 7, no. 1, pp. 114–117, Feb 2018.
[39] T. Y. Al-Naffouri and A. A. Quadeer, “Cyclic prefix based enhanced data
recovery in OFDM,” IEEE Transactions on Signal Processing, vol. 58,
no. 6, pp. 3406–3410, June 2010.
[41] S. Rathinakumar, B. Radunovic, and M. K. Marina, “CPRecycle: Recycling cyclic prefix for versatile interference mitigation in OFDM
based wireless systems,” in Proceedings of the 12th International on Conference on Emerging Networking EXperiments and Technologies,
ser. CoNEXT ’16. New York, NY, USA: ACM, 2016, pp. 67–81.

我们的工作证实了[11]中的结论，即MLP可以在高信噪比中匹配MMSE，并比MMSE更好地处理与CP、剪切噪声和信道不匹配相关的多样性。与[11]不同，我们的信道估计器是线性激活的，而不是使用ReLU，因此可以解释为LMMSE的低秩近似。[11]中的MLP处理没有CP的OFDM波形，而我们的模型使用CP来同时提高信噪比和减轻ISI。 此外，在[11]中，每16位就需要训练一个独立的MLP，而我们只使用一个模型来处理整个相干插槽，从而实现更好的可伸缩性。许多研究使用CNN在OFDM系统[18]、[20]、[44]、[45]中的信道估计，但不能优于理想的LMMSE。然而，对于大规模的MIMO，一个可以优于近似LMMSE[18]的低复杂度信道估计器仍然很有吸引力.[16]中的OFDM接收器实现了线性复杂度O(N)，但只与训练信道模型上的理想LMMSE匹配，在underperforms信道模型上表现不佳。与这些研究相比，我们的DCCN的性能优于理想的LMMSE，其复杂性也只有O(N^2)。在[19]中，基于MLP的非OFDM系统信道估计器在双选择信道中优于近似LMMSE，并且对移动性表现出更好的鲁棒性，这些结果在我们的工作中得到了证实，尽管结果没有直接比较。在[14]中，长期短期记忆(LSTM)用于通过预测未来的数据来估计信道，表明在高速场景中表现优于LMMSE。

[19] Y. Yang, F. Gao, X. Ma, and S. Zhang, “Deep learning-based channel estimation for doubly selective fading channels,” IEEE Access, vol. 7,pp. 36 579–36 589, 2019.

相比之下，我们的方法通过同时处理多个OFDM符号来缓解ISI问题。深度学习能够改进MIMO检测[23]-[25]和信道编码[17]，而本文只考虑了单个天线. Moreover, the aforementioned work [8], [10],
[11], [13]–[16], [23] all rely on explicit DFT/IDFT, which is replaced by a learned linear transform in our approach for increased SNR. 此外，上述工作[8]，[10]，[11]，[13]-[16]，[23]都依赖于显式DFT/IDFT，这被我们的增加信噪比的学习线性变换所取代。我们的工作首先展示了DNNs在处理OFDM波形方面的能力，我们基于OFDM框架结构设置NN层超参数并利用领域知识的方法为其他波形结构提供了一个可转移的设计模板。

III. OFDM COMMUNICATION SYSTEM

三 OFDM通信系统
我们首先介绍了传统OFDM系统底层物理层的相关概念和符号，然后是传统接收器中的信道估计方法。

A. Physical Layer

OFDM通信系统的PHY框图如图2(a)所示。OFDM发射机的输入位首先要进行编码（有冗余），以减少特定信道的误差，编码后的位通过调制在相位和正交（IQ）平面上映射成星座，得到的IQ数据用复数表示。在IQ数据中插入导频和保护频带，形成频域OFDM符号。频域OFDM符号通过反离散傅里叶变换(IDFT)转化为时域，再通过并行到串行(P/S)的转换转化为一维(1D)。循环前缀(Cyclic Prefix，CP)，是将时域IQ数据从末尾的一段复制到时域IQ数据的开头，形成一个完整的时域OFDM符号，如图2(b)所示。然后，基带IQ数据流被向上转换为射频(RF)，并通过RF前端进行空中广播。通过无线信道传播的无线电波被接收机的射频前端接收并下变频为基带数字IQ数据。载波同步器回收时域OFDM符号，并将其发送到基带接收器。

At the receiver, the received time-domain OFDM symbols, ycp, are recovered by a carrier
synchronizer. Then, the CP is removed from ycp and the rest of the IQ samples, y, are transformed to the frequency-domain OFDM symbol, Y, via DFT. Based on Y, a channel equalizer outputs the estimated transmit frequency-domain IQ data ˆX, which is then demodulated to soft bits (log-likelihood) ˜b and converted to binary output bits ˆb by a channel decoder. Finally, ˆb is passed to the next layer. Note that the focus of this paper
is lower PHY, and channel coding is out of the scope. We refer the frequency and time domains in Fig. 2(a) as the IQ domain in which a signal is represented by complex-valued samples.
在接收器处，接收到的时域OFDM符号ycp由载波同步器恢复。然后，从ycp中将CP移除，其余的IQ样本Y通过DFT转换为频域OFDM符号Y。基于Y信道均衡器输出估计的发射频域IQ数据ˆX，然后将其解调到软位（对数似然）˜b，并由信道解码器转换为二进制输出位ˆb。最后，ˆb被传递到下一层。注意，本文的重点是低PHY，信道编码超出了范围。我们参考了图中的频率和时域。2(a)作为用复值样本表示信号的。我们将图2(a)中的频率和时域称为一个信号由复值样本表示的IQ域。

在接收机上，首先去除CP，其余的IQ数据通过FFT转换到频域。信道均衡器估计信道的响应，并对接收到的被衰落信道扭曲的IQ数据进行均衡。接下来，经过均衡的频域IQ数据被解调为软位（浮点数），再由信道解码器将其进一步解码为二进制位。输出的比特流被送到下一层，并回收成数据包。请注意，信道均衡是针对衰减而不是加性高斯白噪声（AWGN）信道的。此外，为了专注于底层PHY的研究，本文忽略了信道编码。
如图2（b）所示，多径传播在接收机处引入了符号间干扰（ISI）。 为了减轻ISI，选择适当的循环前缀长度，使得来自OFDM符号i的ISI在最坏的情况下仅停留在OFDM符号i + 1的CP中。 通常会在OFDM接收器中丢弃CP，以消除ISI。 但是，在大多数情况下，并非所有CP都被ISI污染，因此，可以利用CP作为主信号的冗余来改善接收机性能。 这项工作表明，除了现有的分析方法[24]-[27]，DCCN可以学习利用CP来增强接收机性能。
————————————————

OFDM systems typically have a frame structure where a coherence slot (or “slot” for short) is composed of multiple OFDM symbols, as shown in Fig. 2(b). The notations related to the OFDM coherence slot are as follows: an OFDM symbol contains N subcarriers, where N is the size of DFT/IDFT. Among the N subcarriers, a total of G nullified guard subcarriers are placed at the center (DC guard band) and the edge (edge guard band). A subcarrier in an OFDM symbol is refereed to as a resource element (RE). A coherence slot
contains F consecutive OFDM symbols, in which P and D REs are allocated to pilot and data, respectively. The length of a time-domain full OFDM symbol is S = N +Ncp where Ncp is the length of CP. Under m-ary modulation, an IQ sample carries m bits, and the size of the constellation is 2m.
OFDM系统通常具有帧结构，其中（相干）相连的时段（时隙）由多个OFDM符号组成，如图所示。2(b)。与OFDM相干槽相关的符号如下：一个OFDM符号包含N个子载波，其中N是DFT/IDFT的大小。在N个子载波中，总G无效保护子载波放置在中心（直流保护带）和边缘（边缘保护带）。OFDM符号中的子载波被称为资源元素(RE)。相干槽包含F个连续的OFDM符号，其中P和DRE分别分配给导频和数据。时域全OFDM符号的长度是S=N+Ncp，其中Ncp是CP的长度。在m-调制下，IQ样本携带m位，星座的大小为2^m。

OFDM通信系统通常基于由多个OFDM符号组成的物理帧，如图2(b)所示的一个例子。OFDM帧中参数的符号定义如下。OFDM符号包含N个子载波，其中N是发射机处IDFT的大小。在这N个子载波中，中心（DC保护带）和边缘（边缘保护带）共有G个保护子载波。一个OFDM帧包含多个连续的OFDM符号，它被表示为F，资源单元指的是一个OFDM符号的子载波。对于每个OFDM帧，有P个单元被分配为发射机和接收机都知道的训练信号(先导)，其余D个单元被分配为调制IQ数据。此外，在时域中，循环前缀（CP）是时域OFDM符号的一段副本，它被添加到每个OFDM符号的开头。因此，时域OFDM符号的总长度将从N增加到S，这些参数通常是根据信道特性规定的，如相干时间、相干带宽、总信道带宽等。同时，对于m进制调制，每个星座点包含m位，有2的m次方个星座点。
————————————————

B. Wireless Channel

从数字基带的角度来看，无线信道不仅包括发射天线和接收天线之间的空中传播，还包括射频前端的一切。然而，在本文中，我们只考虑了一个有衰减和噪声过程的无线信道，这是一个公认的简化[20]。无线信道的模型为：
y = x * h + n
其中向量x和y为时域的发送和接收信号，向量h为时域信道系数，向量n为时域白噪声，∗代表卷积。(1)在频域中也可以表示为：Y= X ⊙ H + N0
其中向量X、Y、H、是x、y、h、n的频域变换，如X=DF T(x)。 N0 仍旧是白噪声。 ⊙ \odot ⊙ 代表按元素相乘（两个向量的第i个元素分别相乘）。衰落信道被建模为一条分接延时线，其中信道响应h是一列脉冲响应[20]：

其中，第i个抽头 hi(t)是一个复数，代表信号传播第i条路径的振幅和相位，并且满足$\ \sum_{i=0}^{K-1} ||hi(t)|| ^2 $ = 1。衰减系数因无线电环境不同而不同。如果在一帧内信道系数保持相对恒定，则称为慢速衰减，反之则为快速衰减。虽然从理论上讲，信道系数也可以在OFDM符号内变化，但通常不考虑这种情况，因为假设OFDM帧参数是基于对无线信道的先验知识事先精心选择的。

多路径衰落可以建模为线性有限脉冲响应(FIR)滤波器[51]：

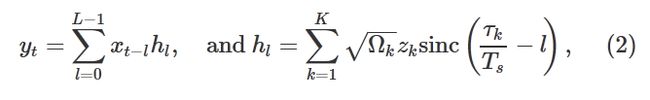
zk是一个复值随机变量，向量Ω和τ表示衰落过程的功率延迟曲线(PDP)，Ts是离散信号的采样周期。选择滤波器长度L，使当l<0或l≥L时，|hl|较小。对于瑞利衰落，zk的实部和虚部是服从高斯随机变量，因此|zk|2遵循瑞利分布。K是多路径衰落信道中的路径数。在平坦衰落信道 K=1中，OFDM符号的所有子载波上的信道系数相同。在多路径衰落信道K>1中，信道系数随子载波而变化，因此信道表现出频率选择性。不同的衰落过程对频域IQ样本的影响如图3所示。请注意， 只考虑噪声和衰落，而信道编码的信道损害则留给未来的工作。
信道脉冲响应h是时变的，其相干时间Tc与最大多普勒频率Fd成反比，即Tc≈1/Fd。An OFDM system is usually configured according to its applications, measured coherence time, T c , coherence bandwidth, B c , and total bandwidth, so that slow fading holds for a coherence slot. OFDM系统通常根据其应用、测量的相干时间、Tc、相干带宽、Bc和总带宽进行配置，以便慢衰落保持一个相干时隙。

C. Channel Estimation and Equalization

考虑一个在接收机上具有导频辅助信道估计的通信系统。不同的导频结构，如块状、梳状和格状的导频，如图4所示[46]，被设计为采样通道失真。导频信号具有恒定信号或低自相关序列（例如，Zadoff-Chu序列）。OFDM系统中的基本导频辅助信道均衡器基于最小二乘(LS)估计器[46]，[47]：

公式3

理想LMMSE估计

表示为[47], [52]:

哪里{mathbfR}{mathbfH}=\mathbfH}，i}{}{mathbf H}，i}^{H}$是信道实现的频域协方差矩阵。
阿尔法是线性域信噪比，
\β\是基于特定调制方案定义的常数。的理想LMMSE估计(4)需要先验信道知识{mathbf R}{\mathbf H}\$和阿尔法，这在实践中是不可用的。
此外，矩阵求逆(4)导致计算复杂度为{mathcal O}(N^{3})。LMMSE的低秩近似[53]理想LMMSE矩阵的逼近左边({mathbf R}}+\frac{\alpha}mathbf{i}})^{-1}经规定阿尔法的奇异值分解(SVD){mathbf R}_{\mathbf H}\$，它可以容忍pdp失配，并实现低复杂度的{mathcal O}(N^{2})以一个不可弥补的误差下限为代价。

LMMSE[53]的低秩近似(LRA)通过RHH的规定α和奇异值分解(SVD)逼近理想的LMMSE矩阵RHH(RHH+βαI)−1，可以容忍PDP不匹配，并以不可约误差下限为代价实现较低复杂度的O(N2)。
对近似LMMSE(ALMMSE)的改进包括使用不同的PDPs[54]、信噪比估计[52]、[55]、秩估计和利用LMMSE矩阵[52]的循环性质。
Fast ALMMSE canfurther reduce the complexity to O(N) with a pre-computedLMMSE matrix at the cost of degraded performance in a
certain SNR range [56].
FastALMMSE[56]可以通过预先计算的LMMSE矩阵进一步将复杂性降低到O(N)，但代价是在一定的信噪比范围内降低性能。

47 J.-J. van de Beek, “Synchronization and channel estimation in OFDM systems”, 1998.
52 W. Zhou and W. H. Lam, “A fast LMMSE channel estimation method for OFDM systems”, EURASIP J. Wireless Commun. Netw., vol. 2009, no. 1, Dec. 2009.

[53]OFDM Channel Estimation by Singular Value Decomposition,1998
56. S. Ohno, S. Munesada and E. Manasseh, “Low-complexity approximate LMMSE channel estimation for OFDM systems”, Proc. Asia Pacific Signal Inf. Process. Assoc. Annu. Summit Conf., pp. 1-4, Dec. 2012.

IV. DCCN-BASED OFDM RECEIVER

基于DCCN的OFDM接收器由一个函数˜b=DS(ycp；Θ)表示，它定义在一个超参数集合S上，用于OFDM帧和DCCN流图的配置(图。5)，其中˜b是传输位的对数似然，ycp是包括CP在内的一致性槽的同步时域接收的OFDM符号，Θ是DCCN的可训练参数的集合。基于DCCN的OFDM接收器包括信道均衡器，然后是基本接收器。DCCN的隐藏层以旧式OFDM接收器中的信号处理模块命名，而它们的功能可能会有所不同。前向网络推广了传统接收机中的信号处理，并通过增加计算冗余来确保Θ的搜索空间至少包含一个ALMMSE接收机，在训练过程中通过引入正则化损失将其最小化。用于研究的流程图中包含了结构冗余，并在第V-E节中提出了一个简化的部署流程图。

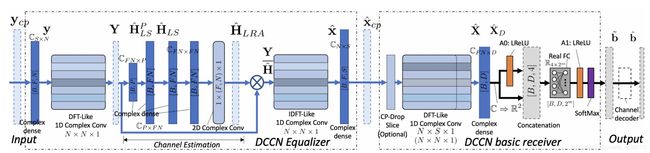
Fig. 5. DCCN OFDM receiver flow graph: a DCCN equalizer converts time domain received signal, ycp, to estimated transmitted signal, xcp, which is subsequently converted to estimated soft bits, ˜b, and hard bits, ˆb, by a DCCN basic receiver. The blue color represents complex-valued domain, and gray for realvalued domain. The dimensions and data types of a dense layer are shown as e.g., CS×N , and the shape of its output tensor as, e.g., [B, F,N], the dimensions of a Conv layer is labeled beside the block, e.g., N × N × 1 represents N 1-D filters each of length N. A dashed block represents a data tensor.
DCCN OFDM接收机流图：DCCN均衡器将时域接收信号ycp转换为估计发送信号xcp，该信号随后被DCCN基本接收机转换为估计软比特˜b和硬比特ˆb。
蓝色代表复值域，灰色代表实值域.
稠密层的尺寸和数据类型表示为CS×N，其输出张量的形状为[B，F，N]，Conv层的维数被标记在块旁边，例如N×N×1表示长度N的每个N1-D滤波器，A虚线块表示一个数据张量。

---

A.复数层指南

不考虑bais偏置和激活函数，复数值神经元可以表示为[34]:

公式5

哪里$x^{IN}，x{out}\in\mathbb{C}$和重量A，b\in\mathbb{R}分别是复权的实部和虚部。(5)的稠密层可以近似于\mathbb{R}_{2\x 2}有接近D的输入和经过训练的权重{mathbf w}\偏左({BEGIN{Small矩阵}a&-b&a End{SmallMatrix}}\右)\End{lined}$。泛化(5)对于更高的维度，我们有以下原则：

注1：
稠密的一层\mathbb{C}{Z{i}\x z_{o}$的稠密层可以随时逼近。\mathbb{R}{2Z{i}\乘以2Z_{o}$有充分的表现力。

注2：
复值卷积(C-Conv)层的尺寸F_{n}\乘以f_{s}\x f_{c}\$(代表F_n}形状过滤器，F_s}的深度F_{c})可以用大小的实值Conv层来近似。$2f_{n}\次数(f_{s}，2)\乘以f_{c}$用于大约-D输入或$2f_{n}\乘以f_{s}\乘以2f_{c}$用于大约-C的输入，不需要以下内容(5)，并且可以通过大小的实值Conv层精确地实现。$2f_{n}\乘以f_{s}\x f_{c}\$通过以下方法输入约-D(5).

通过遵循公式(5)，CVNN层的精确实现减少了不必要的自由度，只需要约简所需的可训练实值权重的一半。更具体地说，1DC-Conv层的三个示例性实现$1\乘以1\乘以1$给出图6(A)说明备注2。所有三个实现都以相同的计算复杂度满足表达需求(每个复杂样本增加四个乘法和两个加法)。前两个近似中的每一个都需要四个权重，而第三个精确的实现只需要两个权重。精确的实现具有较好的空间复杂度和训练效率，减少了优化器的搜索空间。对于从业者来说，如果一个近似的C-Conv层不能满足所需的输入格式或最小的大小，例如滤波器的形状和数目，那么它的表现力就会比精确的C-Conv层要差。对于复值激活原则，我们请读者参阅[34], [35].

Fig. 6. - (a) Three implementations of 1D complex-valued Conv (C-Conv) layer (
$1\times 1\times 1$
) that preserve its expressive power, (b) Implementation of a 1D C-Conv layer (
$8\times 8\times 1$
) based on a 2D real-valued Conv layer (
$16\times (1,8)\times 1$
).
图6.
(A)一维复值Conv(C-Conv)层的三个实现($1\乘以1\乘以1$)保持其表现力，(B)1D-C-Conv层的实现($8\乘以8\乘以1$)基于二维实值Conv层($16\乘以(1，8)\乘以1$).

显示所有

在……里面图6(B)，以一维C-Conv层为例说明了我们的dft类C-Conv层的实现。$8\乘以8\乘以1$由大小的2D实值Conv层实现$16\乘以(1，8)\乘以1$。在这项工作中，复张量的实部和虚部在最后维。

B.基本DCCN接收机
基本DCCN接收机是没有信道均衡器的ofdm接收机，如图5。基本接收器的前向网络从一个可选的切片开始，用于丢弃CP，然后是一个C-Conv层的大小。N乘以S\乘以1(或$N\乘以N\乘以1\n如果CP被删除)，这是为了转换时域ofdm符号，帽子，到频域帽子{\mathbfX}\并利用CP实现信噪比增益。接下来，一个复杂的致密层\x是为了提取所有的数据资源而设计的。帽子{mathbf X}_{D}从一个连贯的插槽。前向网络的其余部分本质上是一个分类器，它将IQ样本转换为软比特，其中输入IQ样本被视为两个实数的向量，\mathbb{C}\右尾\mathbb{R}^{{2}$。提取的IQ向量及其非线性激活，A_0\n，被连成张量的形状。[B，D，4]\并被喂食到一小层密密麻麻的\mathbb{R}_{4次2}{m}$接着是另一个漏出的激活，1美元，其中输出张量被重塑为[B，D，m，2]\然后由Softmax函数沿着它的最后一个维度激活，产生一个软比特–一个向量为±1的似然向量。B是一批输入信号中的插槽数。由于信道编码超出了我们的范围，所以输出比特是通过软比特的硬判决得到的。在……里面第五-E节，对前向网络的变化进行了测试。

C.DCCN信道均衡器
DCCN均衡器，输入为[法][mathbf y]{cp}的输出帽子的基本DCCN接收机，如图5。DCCN均衡器的前向网络包含四个子模块：第一个子模块包括\mathbb{C}{S\x N}(或\mathbb{C}{N\x N}(如果Cp被删除)，则后面跟着一个C-Conv层。KaTeX parse error: Undefined control sequence: \乘 at position 2: N\̲乘̲以N\乘以1\n，它会转换[法…N\乘以N\乘以1\n，和帽子通过添加具有稠密层的cp来恢复\mathbb{C}{N\x S}.

在信道估计子模块中，\x{FN\乘以P}\用于定位导频并估计导频的信道系数。帽子{mathbf H}^{P}{LS}。然后,帽子是通过插值得到的。帽子{mathbf H}^{P}{LS}到接下来三个密集层的整个相干槽和信道估计，以及一个大小为2D的滤波器。(F，N)，类似于上帝抵抗军-LMMSE[53]:开始{方程*}{mathbf H}{上帝军}={mathbf U}{mathbf D}{p}{mathbf U}^{H}{mathbf H}{ls}，标记{6}结束{等式*}
视图源Right-click on figure for MathML and additional features.哪里.=‘class 3’>\是带有项的对角线矩阵。\deltak}=\frac{lambda{k}{\lambda_{k}+\β/\alpha}$为K\in[1，p]\n，和{k}=0为K\in[p+1，N]\n, 马蒂布夫的奇异向量的酉矩阵。{mathbf R}{\mathbf H}\$。而不是设置\粗体符号{\lambda}\$, P, 阿尔法，和马蒂布夫明示[52], [54], [55]中的LMMSE矩阵(6)是从数据中学习的多层稠密层的可训练参数。请注意，这些稠密层的尺寸是一个用于缓解ISI的一致性槽。在……里面第五-C节，我们的dccn接收机还显示了一个像almmse这样的具有指定信噪比的错误层。[52], [53], [55]。其他稠密层数\mathbb{C}{FN\倍\，fn}\$测试第五-E节.

考虑每个相干时隙的OFDM符号数F作为协议中的常数，DCCN接收机的渐近计算复杂度是{mathcal O}(N^{2})(或{mathcal O}(NS)\对于DCCN和CP)，因为DCCN是由级联层组成的，没有任何循环。一维复卷积层和全连通层的最大复杂度为{mathcal O}(N^{2})(或{mathcal O}(NS)(与CP有关)。如果F被视为变量，则复杂性将变为{mathcal O}(N^{2}{2}).

D.2阶段培训
DCCN接收机的训练设置在图7。在线随机生成器创建随机二进制流。.‘>\，将OFDM发射机转换为时域OFDM符号作为发送信号，[mathbf]{cp}$。接收信号[法][mathbf y]{cp}是由一个信道模型创建的，该模型将衰落和噪声添加到马蒂布夫. [法][mathbf y]{cp}和.‘>\分别是培训数据和培训标签。DCCN模型的输出是软比特，\，以及输出位，帽子{\mathbfb}\in\pm 1\，这是由对\。损失函数{mathcal L}({mathbf b}、\tilde{mathbf b}、\hat{mathbf b}、\粗体符号{Theta})$是交叉熵(CE)损失和正则化损失的加权和。{mathcal L}{reg}(\粗体符号{\Theta})$:开始{{mathcal L}({mathbf b}，\tilde{mathbf b}，Hat{mathbf b}，\bold符号{\Theta})={mathcal L}{CE}({mathbf b}，\dide{mathbf b}+varepsilon{mathpsilon{mathbf b}，\varepsilon{mathpsilon{mathbf}(\bold符号{Theta})，\Tag{7}结束{等式*}
视图源Right-click on figure for MathML and additional features.哪里\varepsilon\ll 1是一个小常数。交叉熵损失，{mathcal L}{CE}({mathbf b}，\tilde{mathbf b})$，是训练标签的平均交叉熵。.‘>\，以及软比特\。在训练期间，符号{\Theta}接收端随机初始化并由adam优化器进行更新，该优化器基于(7).

Fig. 7. - Block diagram of the DCCN training System.
图7.
DCCN训练系统框图。

显示所有

由于DCCN接收机存在严重的失真，在多径衰落信道中直接训练DCCN接收机是困难的，也是不切实际的。图3©。因此，如图8，分两个阶段对基本接收机和均衡器进行训练。在第1阶段中，基本接收机仅在AWGN信道中进行训练。在第二阶段中，DCCN均衡器的流程图首先在TensorFlow会话中被预先训练的基本接收机占优势，用于图形编辑。然后，在另一个会话中加载和训练均衡的DCCN接收机，其中冻结基本接收机的可训练参数，并包括信道衰落以生成训练数据。在第一阶段和第二阶段，损失函数是相同的。当前向网络的下半部分被冻结时，图形编辑技术可以实现反向传播。请注意，两级训练方法可以通过在第2阶段重用相同的预训练基本接收机来提高数据效率，以适应不同的衰落设置。同样，第二阶段的训练模型也可以针对不同的实际频道进行微调.

Fig. 8. - Training the basic receiver and the equalizer in two stages.
图8.
训练基本接收机和均衡器分两个阶段。

显示所有

为了提高训练效率，采用了多种技术。训练数据以小批的形式输入模型，利用图形处理单元(GPU)中并行处理的高吞吐量，最大限度地减少内存复制的延迟。在基于NumPy的OFDM发射机和衰落模块的编程中，数据处理是矢量化的，避免了大循环。随着训练的进行，学习速率呈指数衰减，以进行微调.随机训练标签和相应的训练数据是在线生成的，而不是重复输入预先生成的训练数据集。因此，我们使用迭代法而不是一个时代(在整个数据集上进行完整的训练)来描述训练中最外层的循环。如果关键性能度量(即BER)在一定次数的迭代后没有改进，则在最大训练迭代次数的基础上使用早期停止机制来结束训练。

E.培训中的渠道设置
对于基于DL的PHY的训练信噪比的设置，没有明确的指导。在这两个阶段，我们使用不同的信噪比配置。在第一阶段，信噪比并不影响最优的基本接收机，而是影响训练的有效性。信道中的噪声会产生比特误差，从而驱动梯度下降，并起到正则化的作用，以防止过度拟合。较高的信噪比要求更大的小批处理来产生同样数量的误码，从而降低数据效率，延长训练的收敛性。另一方面，低信噪比可以在相对大的BER中隐藏小的解调偏差，即在输出比特中始终比−1s多1s。为此，我们建议训练信噪比值为E_{b}/N_{o}=5达布[21]对于训练阶段1，具体来说，信噪比埃塔=500万美元选择DB为百万-数字调制。

在训练阶段2，最优DCCN均衡器依赖于信道统计量，如信噪比和PDP。为了使训练后的模型具有更好的通用性，采用了信噪比和衰落模型相结合的方法。在不排除中、低信噪比值的情况下，从工作信噪比系统中随机选取每个OFDM相干时隙的信噪比。例如,\eta_{i}\in\0，3，{\dots}，30\$带着P(\ETA_{i}\geq 17)=90%。其基本原理是DCCN均衡器类似于一种快速ALMMSE算法。[52]，它在高信噪比(即20 dB)设计时比低信噪比(5dB)具有更好的性能。同时，由于LMMSE对PDP失配具有较强的鲁棒性，因此DCCN均衡器对于不同PDPs的最优点将被紧密定位。瑞利衰落模型的混合不仅提高了广义化，而且提高了收敛时间。具有较短时延扩展的衰落模型可以平滑整体损失情况，帮助优化器克服与多径较丰富的衰落相关的局部极小值。在……里面第五至D节和V-E比较了两个阶段不同信道设置的训练模型。

第五节评价结果
A.方法
将DCCN接收机与具有不同信道估计量的传统接收机进行了比较。[43]在数值评估中。我们首先给出了DCCN基本接收机的结果。百万-正交幅度调制(QAM)调制M\leq 4在AWGN信道中，在不同PDP、ISI泄漏和移动性的瑞利衰落信道中，均衡DCCN接收机。我们分别用符号DCCN和DCCN-CP来表示DCCN接收机的非CP开发和CP开发.

评估后的ofdm系统模拟了一种简化的lte下行帧结构。[57]详见表一其中DFT的大小为64，边缘和直流的保护子载波总数为16，采样率为0.96 MHz，子载波的带宽为15 kHz。一个相干时隙包含7个ofdm符号，其中分配给导频和数据的res数为P=16和D=320分别。一种分散的导频模式，它与LTE协议一致，如图4，并且导频信号的恒定值为\sqrt{1/2}(1+i)$。星座映射采用2、4、8、16阶QAM和灰色码，星座的最大幅值为1，发射后OFDM波形的峰均功率比(PAPR)限制在9dB以内。

表一评估OFDM系统的配置
Table I
基本接收机和均衡器的训练配置百万-元调制列于表二。一种基于随机梯度下降的ADAM优化器，其最小批量大小为72个相干性槽。在每次迭代中，通过遗留的OFDM发射机和信道模型生成新的随机比特流(训练标签)并将其转换为训练数据。由于训练标签是随机的，所以早期停止机制的损失函数是基于训练数据而不是单独的测试数据集。训练结束时要么达到最大的迭代次数，要么触发早期停止，这通常发生在实践中。最初将学习率设置为0.001，每500个小批(步骤)或2.5个外部迭代降低2%。中的描述来设置信噪比。第四-D节。每个外部训练迭代包含200个小批，每个信噪比点从−10到30 dB的测试数据为20,000个相干时隙。训练阶段2的瑞利衰落是连续时隙中平坦衰落、EPA、EVA和ETU的交替模型。

表二$100万的培训配置-Ary调制
Table II
训练DCCN模型持续250-1300次迭代，如图9。训练过程从一个快速拟合开始，然后是一个长的微调阶段：交叉熵首先在前10-50次迭代中急剧下降，然后缓慢但稳定地下降，直到到达地板。源代码可在[43].

Fig. 9. - Evolution of cross entropy loss in the training of DCCN models.
图9.
DCCN模型训练中交叉熵损失的演化

显示所有

B.加性高斯白噪声信道
我们的基本接收机和遗留的OFDM接收机[43]在信噪比为10~20 dB的AWGN信道中，对BPSK、QPSK、8 QAM和16 QAM进行了调制。图10，其中DCCN-CP考虑长CP。由于DCCN在AWGN信道中是最优的，没有CP的帮助，我们不期望DCCN优于传统的解调。对于BPSK、8 QAM和16 QAM，当误码率低于0.16 dB时，DCCN与遗留接收机的间隔(≤0.16 dB)非常接近10−5 。然而，对于QPSK，DCCN开始在10−2 在误码率为0.7dB的情况下，空隙增大到0.7dB。10−6 。另一方面，DCCN-CP的性能一直优于DCCN，从BPSK的0.7 dB下降到16 QAM的0.5 dB。对于qpsk，dccn-cp在10−6 。注意，当误码率很小时，例如，\leq 10{-5}，由于仿真中数据大小有限，相对误差增大。Cp在所有子载波上携带信息，并经历独立的随机噪声，从而从理论上提高数据信号的功率。{N_{cp}}/(FN^{2})$，对应于在AWGN信道中CP长度为0.75dB的信道信噪比增加0.75dB。0.25N。对于BPSK，DCCN-CP使DCCN的信噪比提高了近0.75 dB.结果表明，利用C-Conv层将时域OFDM符号转换为频域具有利用CP承载的冗余的优点，而这种冗余不能通过显式DFT来实现。

Fig. 10. - BER of legacy and DCCN OFDM receivers vs SNR, in AWGN channel, with long CP.
图10.
传统的BER和DCCN OFDM接收机对信噪比的影响，在AWGN信道中，具有较长的CP。

显示所有

C.瑞利衰落信道
其次，对瑞利衰落信道中的均衡DCCN接收机进行了评估。基准是传统的具有不同信道估计量的ofdm接收机：LS估计器(LS样条)，基于cp的LS估计器。38，理想的LMMSE和ALMMSE。对于理想的lmmse，每个ofdm符号都更新信道协方差矩阵，如{mathbf R}{mathbf H{\mathbf H}={mathbf H}，i}{{}{mathbf H}{，i}{H}基于真信道实现\，以及ALMMSE的每个时隙{mathbf R}{mathbf H}=\frac{1}{f}{ls}^{mathbf H}{LS}{mathbf H}^{H}。这个帽子{mathbf H}{LS}在理想的LMMSE和ALMMSE是从LS样条.测试的ALMMSE表示复杂性ALMMSE的上界。{mathcal O}(N^{2}) [52]全秩近似和完全信噪比估计。ISI被设置为仅在同一相干时隙中的连续ofdm符号之间。为了简单起见，在接收机中考虑BPSK调制和完全同步。每个相干时隙都生成独立的信道实现，默认情况下在时隙内保持不变(F{d}=0\n(赫兹)[11]。如果F_{d}>0\nHz，时变信道是由杰克模型和48个正弦波和衰落技术产生的。[59]。平坦衰落和3 GPP多径衰落模型[58]都是经过评估的。DFT大小为64，信道滤波器长度，升对于平坦衰落，扩展行人A模型(EPA)、扩展车辆A模型(EVA)和扩展典型城市模型(ETU)分别为1、9、11和13。

在小时延扩展的瑞利衰落信道中，如平坦衰落和EPA模型等。[58]文中给出了均衡DCCN接收机的误码率性能和长CP的基准测试结果。图11(A)和11(B)分别。自信道滤波器长度升如果小于CP 16的长度，则可以通过丢弃CP完全消除ISI。与理想的LMMSE相比，降低CP的DCCN接收机在低到中信噪比(≤15 dB)范围内性能相似或略好，在高信噪比下性能较差，在平坦衰落时性能差距很小，在EPA信道中的性能差距较大1~3dB。DCCN-CP接收机的性能比理想的LMMSE高约1dB，在低到中信噪比范围内几乎与理想信道估计的理想接收机重叠，但在高信噪比下性能也有所下降。结果表明，DCCN-CP接收机能够利用CP中承载的冗余信息来获得性能增益。尽管dccn-cp接收机与这里的完美信道估计值不谋而合，但它的性能增益实际上取决于cp中的冗余量，这一点将在后面讨论。图13。与平坦衰落相比，EPA信道中的时延扩展使理想LMMSE和ALMMSE之间的性能差距从0.8增大到1.4 dB，ALMMSE与LS样条之间的性能差距从0.7 dB扩大到1dB，而LS-CP与ALMMSE的距离接近于ALMMSE。虽然LS-CP比ALMMSE低0.2 dB，但LS-CP不需要先验信息，而ALMMSE是基于完全信噪比的.请注意，在实际工作中，信噪比为30 dB并不常见，测试误码率的不确定度在10−4 也更高。当ISI完全消除时，DCCN的性能与理想的LMMSE相似，它具有信道协方差矩阵的先验知识，这表明DCCN可以从数据中学习信道统计信息。

Fig. 11. - BER of equalized DCCN receivers and benchmarks with long CP
$N_{cp}=16$
in low-mobility Rayleigh fading channels: (a) flat fading
$L=1$
, and (b) multipath fading with low RMS delay spread (EPA [58]),
$L=9$
.
图11.
长CP均衡DCCN接收机的BER和基准N_{cp}=16在低移动瑞利衰落信道中：(A)平坦衰落L=1和(B)低均方根时延扩展的多径衰落(EPA)[58]), L=9.

显示所有

Fig. 12. - BER of equalized DCCN receivers and benchmarks with short CP
$N_{cp}=4$
in multipath Rayleigh fading channels with large RMS delay spread and leakage of ISI: (a) EVA [58]
$L=11$
, and (b) ETU [58]
$L=13$
.
图12.
短CP均衡DCCN接收机的BER和基准N_{cp}=4在多径瑞利衰落信道中，具有较大均方根时延扩展和ISI泄漏的多径瑞利衰落信道：(A)EVA[58] L=11，(B)ETU[58] L=13.

显示所有

Fig. 13. - BER of DCCN receivers with different CP lengths vs SNR in flat fading channel. The DCCN equalizer is trained only in flat fading channel. The gains of DCCN-CP receiver with long CP (
$25\%N$
) and short CP (
$7\%N$
) are 0.88 dB and 0.33 dB, respectively. The DCCN receiver that drops CP is on average 0.5 dB worse than the receiver with known channel information. Legacy receiver with CP-enhanced LS equalizer [38] gains 0.7 dB and 0.3 dB over baseline LS equalizer in long and short CPs, respectively.
图13.
在平坦衰落信道中不同CP长度与信噪比的DCCN接收机的BER。DCCN均衡器仅在平坦衰落信道中训练。长CP的DCCN-CP接收机增益25美元)和短CP(7美元)分别为0.88dB和0.33dB。下降CP的DCCN接收机比信道信息已知的接收机平均差0.5dB。具有cp增强LS均衡器的遗留接收机[38]在长和短CPS中，比基线LS均衡器分别提高0.7 dB和0.3 dB。

显示所有

在具有大时延扩展的多径信道中，如EVA和ETU模型[58]文中给出了具有短CPS的均衡DCCN接收机和基准的信噪比误码率性能。图12(A)和12(B)分别。值得注意的是，在信道长度超过CP长度的情况下，即使有完善的信道知识，也不能通过丢弃CP来消除ISI，从而导致在高信噪比环境下的性能下降。在存在isi的情况下，理想lmmse在中高信噪比范围内的性能优于LS和所有其他信道估计器，类似的结果在[60]。同时，通过减少频率选择性衰落中的频率缺口。[38]在基线LS估计上，CP增强LS估计器的性能增益随着信道的延迟扩展而增加。在具有大时延扩展的频率选择性信道中，DCCN接收机的性能优于ALMMSE、LS和CP增强LS，在高信噪比范围内有很大的裕度，例如，在BER为0.01时，引导ALMMSE比ALMMSE高5 dB。DCCN均衡器可以利用处理整个相干时隙而不是单个OFDM符号的优点，从而进一步降低ISI。在传统的cp增强均衡器中也采用了类似的机制。[38]，其中前一个OFDM符号的解码数据用于减少下一个OFDM符号的ISI。DCCN可以学习在频率选择性衰落信道中共同降低ISI和频率抵消，通过协同产生优异的性能。与之相比，cp-增强方法在[38]在实验中只能提高基线LS估计，但不能改善理想的LMMSE和ALMMSE。

测试接收机在双选择性信道中的Bers，包括在EVA和ETU信道中的多普勒扩展，用虚线显示在图12(A)和12(B)。在移动信道中，多普勒效应增加了信道的时间变化，导致频散，导致OFDM接收机的载波间干扰。当最大多普勒频率为70 Hz时，理想的LMMSE、ALMMSE和DCCN-CP在中等到高的信噪比中分别上升了0.003、0.0008和0.001。DCCN-CP仍然领先于类似于静态情况的空白.然而，在ETU信道中，最大多普勒扩展为300 Hz时，理想的LMMSE、ALMMSE和DCCN-CP的BERS分别上升了0.007、0.01和0.018，其中DCCN-CP受影响最大。这些结果表明，DCCN-CP对信道移动性具有较强的鲁棒性，但在较低的导频密度为4.7%的情况下，其相对于传统接收机的优势在高移动性情况下会受到影响。

均衡DCCN接收机和CP增强LS接收机CP增强的有效性[38]在具有长和短cps的ofdm系统中进行评估，如图13。为了公平的比较，选择平坦衰落信道，因为没有ISI将泄漏到主OFDM符号短CP。均衡DCCN接收机仅在旗标衰落信道中进行训练。无论CP长度如何，下降CP的基线DCCN和LS接收机都具有相同的性能。在长CP和短CP的设置下，DCCN-CP接收机分别提高了0.88 dB和0.33 dB，cp增强的遗留LS接收机分别提高了0.88 dB和0.33 dB。[38]分别提高0.7 dB和0.3 dB。DCCN-CP接收机利用CP比传统方法略有效。[38].

D.概括性
DCCN和基准在不同渠道的评价第五-C节已经表明，经过训练的均衡化DCCN接收机可以很好地推广到不同的衰落信道。为了进一步说明不同的训练设置对DCCN的通用性的影响，我们给出了在混合瑞利衰落信道中训练的dccn-cp接收机在所有四种不同衰落信道中训练的误码率。L=12，与在单个瑞利衰落信道中训练的其他四个dccn-cp接收机进行比较，然后在相同的衰落模型中进行测试，以保持其他一切相同，如图14。当信噪比为5dB时，在混合衰落信道上训练的接收机性能优于在单多径衰落信道中训练的接收机，但在混合衰落模型中训练的≥-CP接收机的性能比仅在平坦衰落信道中训练的接收机平均低0.5dB。混合衰落模型可以帮助DCCN在训练过程中克服局部极小值，而不是在具有大延迟扩展的单衰落模型中训练，如下所示图14，在平坦衰落中以精度为代价。在混合衰落条件下训练的dccn-cp接收机的优点也可以推广到未见的pdp(绿色曲线)。图14).

Fig. 14. - Comparison of DCCN equalizers trained with mixed Rayleigh fading models vs trained with single channel model and tested on the same channel model, the four Rayleigh fading models are: flat fading, EPA, EVA, ETU [58].
图14.
混合瑞利衰落模型训练的DCCN均衡器与单信道模型训练并在同一信道模型上测试的DCCN均衡器比较：平坦衰落模型、EPA模型、EVA模型、ETU模型[58].

显示所有

E.烧伤研究和替代培训方法
我们测试了DCCN基本接收机的6种替代结构，(A\a–F\f)，更改了6个组件中的一些。它们在AWGN信道中的4种调制的详细结构和测试结果如下所示表三(-：包括，X：删除，✓：测试通过，F：测试失败)。两个连续的Conv层位于Leakerelu之前。A_0\n。除\c和\d，其他4种方案的性能与原方案相同。流图A\a表明DFT样的C-Conv层可以被致密层所代替。\mathbb{C}_{S\x N}。在流程图中出现了较大的误差层。\c和\d，这表明只有IQ向量(\c)或其漏出的再激活(\d)无法取代它们的组合，然而，它们可以被线性卷积所取代，这种卷积扩展了来自\mathbb{R}^{{2}到\mathbb{R}{2}{m}}然后是非线性激活。F\f。替代E显示了最后的漏出激活是不必要的，尽管它改善了训练。非线性激活A_0\n帮助减少可训练参数的数量，如原始流图中所示。

表三DCCN基本接收机的可选流程图及测试结果
Table III
接下来，我们修改\mathbb{c}{FN\乘以FN}在DCCN-CP均衡器中，从0(DCCN-CP-L1)到3(DCCN-CP-L4)，去除2D C-Conv层.DCCN-CP-L1和DCCN-CP-L2的性能优于EVA信道中的2层和3层(L3、L4和原始层)，如图15，在EPA通道中有类似的性能。它显示出两层稠密的\mathbb{c}{FN\乘以FN}和原来的一样，它对性能和复杂性都是最好的。还证明了用两个分离的Conv层代替C-Conv层来实现对实部和虚部的过简化处理，不能成功地训练DCCN，即误码率为0.47。

Fig. 15. - BER performance of DCCN-CP receivers (short CP) with different hyperparameters or training SNRs in EPA and EVA channels.
图15.
不同超参数或训练信噪比的DCCN-CP接收机在EPA和EVA信道中的BER性能。

显示所有

我们还测试了两个阶段的不同训练方法。在第一阶段，信噪比为20 dB的dcn-cp在AWGN信道中比基线低2dB，如图16。在第二阶段，相同的初始模型在信噪比分别为5和20 dB的混合衰落信道中训练，其误差层(0.0003)大于混合信噪比训练的基线，如图16。最后，通过将两个阶段的信道和snr混合在一起，将dccn-cp训练成一个阶段，可以显著降低性能，即误码率增加0.01，如DCCN-CP(1级))在图16在EVA频道。这些结果证明了我们的两阶段训练方法和设置是合理的.

Fig. 16. - Simplified DCCN-CP receiver for deployment, using legacy data REs extraction and demodulation, trained in single stage (stage 2).
图16.
简化的DCCN-CP接收机的部署，使用遗留数据的区域提取和解调，训练在单级(第2阶段)。

显示所有

中的dccn-cp接收器结构。图5可以通过用遗留数据提取和解调替换DCCN基本接收机来进一步简化，如图16…相比较[11]简化的DCCN-CP接收机不需要显式DFT，可以利用CP来提高性能.

第六节。结论与未来工作
本文提出了一种端到端OFDM接收机–深复值卷积网络(DCCN)，用于从同步时域OFDM信号中恢复未编码比特.DCCN不把IQ样本的实部和虚部看作分离流，而是遵循复域乘法规则，可以代替OFDM系统中的DFT/IDFT，利用OFDM波形中循环前缀的冗余来提高信噪比。利用复值神经网络的表现力和协同优势，dccn能够将cp开发、lmmse的低秩逼近和码间干扰抑制等任务结合起来，从而在双选择性瑞利衰落信道中优于传统的cp增强信道估计和lmmse的传统接收机，具有更低的计算复杂度。{mathcal O}(N^{2})。这项工作也为类似工作提供了可转移的经验。为复杂值卷积网络的近似实现提供了实用的指导思想，特别是针对OFDM系统的参数设置卷积层的维数。针对基于深度学习的无线收发信机，提出了一套新的训练方法，包括一种传输学习方案，一种能防止训练中梯度问题消失的端到端损耗函数，以及使用混合信噪比和衰落模型来平滑损失的方法。证明了深层神经网络处理复杂通信波形的能力，并提出可以用硬件AI加速器代替OFDM接收机中的FFT处理器。

复杂值神经网络未来可能的发展方向包括：1)探索非线性信号处理以获得更好的性能和(或)复杂度；2)利用卷积层来提高信道估计的可扩展性；3)扩展到大规模MIMO等空域；4)利用基于复值神经网络的通信自动编码器研究波形设计和信道编码。