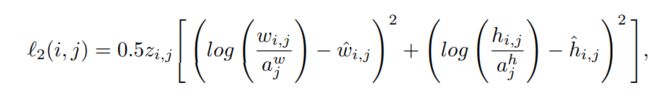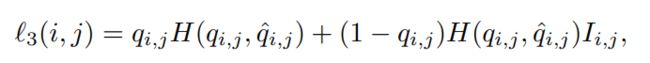【论文】Poly-yolo: 改进anchor分配问题

Poly-yolo: higher speed,more precise detection and instance segmentation for yolov3

Poly-YOLO建立在YOLOv3的原始思想的基础上. 本文的贡献
1、修改了骨干网络增加CE模块
2、修改了标签分配的逻辑，avoid to miss the training with close object at small feature map.
3、修改了输出层，融合特征图后在进行回归，适应在单一的检测场景中提升更好的性能。
4、多边形检测

1 修改了骨干网络增加CE模块

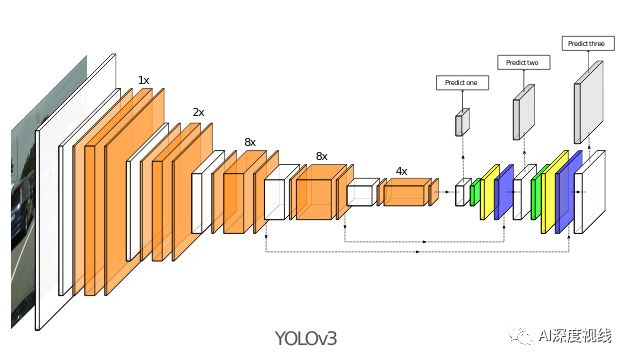
修改YOLO架构，是在主干中使用squeeze-and-excitation(SE)块。像其他许多神经网络一样，Darknet-53使用重复块，其中每个块由卷积和跳连组成。(SE)块允许使用空间和通道的信息，这带来准确性的提高。通过(SE)块和提高输出分辨率，降低了计算速度。由于速度是YOLO的主要优势，为了平衡我们在特征提取阶段减少了卷积滤波器的数量，即设置为原始数的75%。

此外，neck和head较轻，共有37.1M的参数，明显低于YOLOv3(61.5M)。不过，Poly-YOLO比YOLOv3的精度更高。

再者，我们还提出了poly-yolo lite，旨在提高处理速度。在特征提取器和head中，这个版本只有Poly-YOLO66%的滤波器数量。最后，s1减到1/4。yolo lite的参数个数为16.5M。

2 重写标签

由于YOLO系列都是基于图像cell栅格作为单元进行检测，以416416大小的图像为例，在图像分辨率随着卷积下降到1313的特征图大小时，这时候特征图一个像素点的感受野是32*32大小的图像patch。而YOLOV3在训练时候，如果出现相同两个目标的中心位于同一个cell，那么前面一个目标就会被后面目标重写，也就是说两个目标由于中心距离太近以至于在特征图上将采样成为同一个像素点的时候，这时候其中有个目标会被重写而无法进行到训练当中。

label重写问题：不会在原分辨率大小时候发生，本文的关注点是在尺度scale=1/8，1/16，1/32的尺度上的情况。

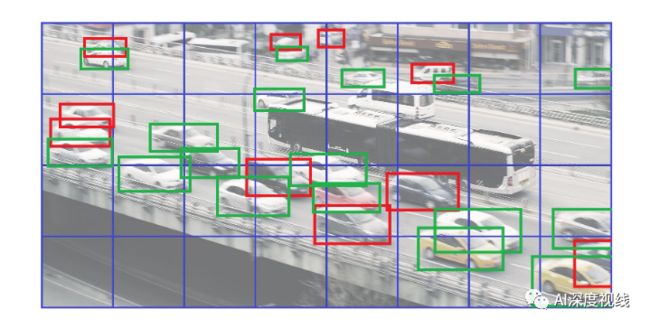
如下图所示，红色目标为因为重写而没有加入到训练中的目标，可以看到，在这样一个特征图上，重写的目标数量还不少，27个目标里有10个都被重写，特别是比较稠密的地方。

3、修改了输出层

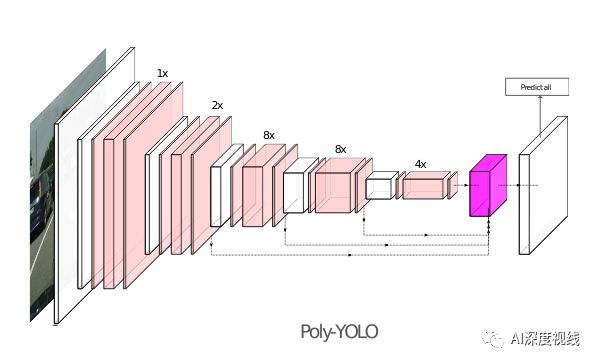
上图显示了原始体系结构和新体系结构之间的比较。Poly-YOLO在特征提取器部分每层使用较少的卷积滤波器，并通过squeeze-and-excitation模块扩展它。较重的neck block被使用stairstep进行上采样、带有hypercolmn的轻量block所取代。head使用一个而不是三个输出，具有更高的分辨率。

3.1 修改细节

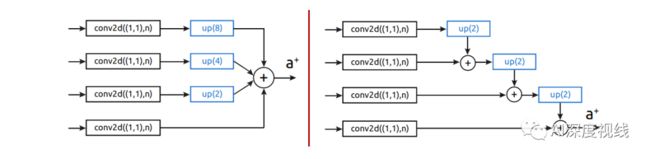
使用hypercolmn实现对于多个尺度部分的单尺度输出合成：
设O是一个特征图，u(·ω)函数表示以因子ω对输入图像进行上采样，m(·)函数表示一个转换，把a×b×c·转为a×b×c×δ维度的映射，δ是一个常数。此外，认为g(O1，…，On) 是一个n元的composition/aggregation函数。为此，使用hypercolmn的输出特征图如下所示：

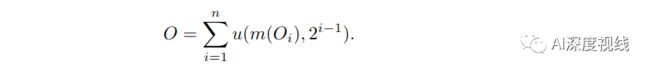
从公式中可以明显看出，存在着很高的不平衡:

• 一个$O_1$的单值投影到O的单值中，
• 而$O_n$的单值却直接投影成$2^{n-1}$的值中。

为了打破这种不平衡，我们建议使用计算机图形中已知的staircase方法，
staircase插值增加(或降低)图像分辨率最大10%，直到达到期望的分辨率。与直接上采样相比，输出更平滑。这里使用最低可用的upscale因子2。形式上定义staircase输出特征映射O '为：

参见下图:

如果我们考虑最近邻上采样，O=O '保持不变。对于双线性插值(和其他)，O/=O '用于非齐次输入。关键是，无论是直接上采样还是staircase方法，计算复杂度都是相同的。虽然staircase方法实现了更多的添加，但它们是通过分辨率较低的特征图计算的，因此添加的元素数量是相同的。

3.2 修改目的：改进anchor分配问题

YOLOv3中采用kmeans算法聚类得到特定的9个anchor，并且以每三个为一组，大尺度的特征图负责预测小物体，中等尺度和小尺度的特征图负责预测大物体。一个特定的GT框与哪个scale的anchor匹配度最高，就会被指定给哪个scale，正常情况下应该是不同大小的物体会被anchor分配到不同预测层进行预测。

但是这种分配机制只适用于标准分布M~U(0,r)，均值u=0，标准差σ^2 = r

然而，在实际问题中，均值u=0.5r，标准差σ^2 = r是一个更现实的情况，这将导致大多数box将被中间输出层(中等大小)捕获，而其他两个层将未得到充分利用。

为了说明这个问题，假设两个box：m1和m2；前者与放置在高速公路上的摄像头的车牌检测任务相连接，后者与放置在车门前的摄像头的人检测任务相连接。
对于这样的任务，我们可以获得：

• m1∼(0.3r,0.2r)，因为这些牌将会覆盖小的区域，
• m2∼(0.7r,0.2r)，因为人类将会覆盖大的区域。

对于这两个集合，分别计算anchor。第一种情况导致的问题是，中、大型的输出规模也将包括小的anchor，因为数据集不包括大的目标。这里，标签重写的问题将逐步升级，因为需要在粗网格中检测小目标。反之亦然。大目标将被检测在小和中等输出层。在这里，检测将不会是精确的，因为中小输出层有有限的感受野。三种常用量表的感受野为{85×85,181×181,365×365}。这两种情况的实际影响是相同的：性能退化。

在介绍YOLOv3的文章中，作者说:“YOLOv3具有较高的小目标AP性能。但是，在中、大型目标上的性能相对较差。” 我们认为YOLOv3出现这些问题的原因就是在此。

anchor分布问题，有两种解决办法：
第一种方法：
 kmeans聚类流程不变，但是要避免出现小物体被分配到小的特征图上训练和大目标被分配到大输出特征图上面训练问题，具体就是首先基于网络输出层感受野，定义三个大概范围尺度，然后设置两个阈值，强行将三个尺度离散化分开；然后对bbox进行单独三次聚类，每次聚类都是在前面指定的范围内选择特定的bbox进行，而不是作用于整个数据集。主要是保证kmeans仅仅作用于特定bbox大小范围内即可。但是缺点也非常明显，如果物体大小都差不多，那么几乎仅仅只有一个输出层有物体分配预测，其余两个尺度在“摸鱼”。

第二种方法：
 创建具有单个输出的体系结构，所有物体都是在这个层预测。可以避免kmeans聚类问题，但是为了防止标签重写，所以把输出分辨率调高。作者采用的事1/4尺度输出，属于高分辨率输出，重写概率很低。（创建一个具有单个输出的体系结构，该输出将聚合来自各种scale的信息。然后一次性处理所有的anchor。）
本文是采用第二种处理方法进行优化

4 检测多边形 Instance segmentation with Poly-YOLO

v3的作者说框狠傻逼我也狠喜欢掩膜但我没法应用到YOLO中。我们搞出来了一个让YOLO能做实例分割但是没有对速度有巨大负面影响的方法。在我们之前的工作[1]，我们专注于通过不规则四边形的方式让YOLO有更高准确率。我们证明了不规则四边形的方式能收敛更快，并且分类上四边形近似比矩形近似能有更高的准确率。限制在于顶点数量只能有4个。我们这里介绍了一种不需要使用递归神经网络的多边形能够使用多个顶点去检测目标的方式并且也不会减慢检测速度。
与Poly-YOLO集成(实例分割和目标检测集成)

检测多边形的思想是通用的，可以很容易地集成到任意的神经网络中。通常，必须修改三个部分：数据准备的方式、体系结构和损失函数。在Poly-YOLO中，输出层中卷积滤波器的数量必须更新。当我们只检查box时，最后一层输出维度为n=na(nc +5),na=9(anchor的个数)，nc为类别数。对基于多边形的目标检测进行集成，得到n=na(nc+5+3nv)，nv为每个多边形检测到的顶点数的最大值。

损失函数如下图所示：

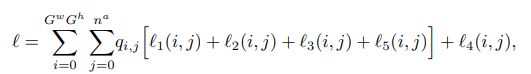
l1(i,j)是对边界框中心预测的损失；
l2(i,j)是对框的尺寸的损失；
l3(i,j)是置信度的损失；
l4(i,j)是类别预测的损失；
l5(i,j)是由距离、角度和顶点置信度预测组成的边界多边形的损失。最后，qi,j∈{0, 1}是一个常数，指示第
个单元格和第j个锚点是否包含标签。
l1到l4都是和YOLOv3一样，l5是Poly-YOLO基于多边形预测扩展出来的。

4.1 The principle of bounding polygons

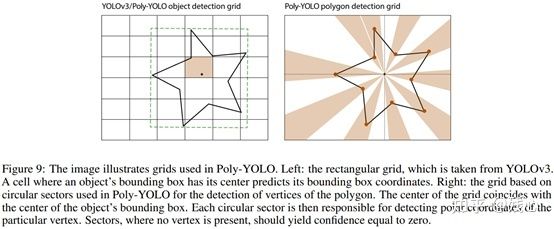
YOLOv3使用垂直网格，每个网格都能检测回归框，或者多个锚框中的回归框。我们用一个增加的极坐标子单元扩展每个网格，就像Figure 9中展示的那样。

v3中的回归框被描述为bi = (bix1，biy，bix2，biy2)，也就是左上和右下，我们扩展了这个元组，即bi = (bix1，biy，bix2，biy2，Vi)，Vi = {vi0，…，vin}是一个给定目标的n个极单元的一组多边形顶点。vij = {αij，βij，γij}，α和β是一个顶点的极坐标，γ是置信度。如果没有坐标存在于一个极单元，那么置信度为0，否则为1。

在常见数据集中，许多物体可以被用相似的形状覆盖因为他们经常被从相似的视角观察，区别在于目标大小而已。比如车牌，手势，人，车，几乎都有相似的形状。通用形状可以很容易被极坐标表示，这也是我们选择极坐标而不是围绕多边形的笛卡尔方法的原因。

αij表示顶点到原点的距离，βij表示角度。中心点的确定使用旧方法。我们将α归一化使用顶点到原点的距离比上回归框的对角线。

推理时，可以通过αij乘以回归框对角线取得的值来得到顶点距离原点的距离的绝对值。

这套方法让网络学习大小无关的、通用的案例，而不是大小依赖的案例。举个例子，同一辆车被放到不同的距离拍下两张照片，图片上的大小会不同，并且模型预测的各种值，置信度，角度，顶点的相对距离，两张图片都相同。当目标被检测到时，顶点到原点的距离会被乘以回归框对角线距离，两套具体值会得到，与需要直接预测每个目标的具体值的PolarMask[25]对比，这种分享的方法能使得学习更加容易。

进一步的提升也是可能的。对于βij属于[0,360]来说，可以改变为βij属于[0,1]这种线性转换。因为我们的极坐标被分为极单元，可以专注于每个单元内部的角度间隙。当一个极单元有高置信度时说明一定有顶点在其中，那么我们使用βij属于[β1，β2]来表示，其中βij1和βij2是顶点可能存在的角度的最低值与最高值。接着我们在线性转换时令βij1=0和βij2=1。以上方式就能知道顶点准确的位置。

4.2 Integration with Poly-YOLO

检测边界多边形的想法是通用的，可以很容易地集成到任意神经网络中。 一般来说，需要修改三个部分：准备数据的方式、架构和损失函数。 有关从语义分割标签中提取边界多边形，请参见第 5.1 节。 提取的边界多边形必须以与边界框数据相同的方式进行扩充。

必须修改架构以产生预期的值。在 Poly-YOLO 的情况下，必须更新输出层中卷积滤波器的数量。当我们只检测边界框时，最后一层由 n = na(nc + 5) 卷积滤波器表示，其内核维度为 (1, 1)，其中 na 是锚点的数量（在我们的例子中是 9 个）和 nc代表多个类。在集成基于多边形的对象检测的扩展后，我们得到 n = na(nc + 5 + 3nv)，其中 nv 是每个多边形检测到的最大顶点数。我们可以观察到 nv 对卷积滤波器的数量有很大的影响。例如，当我们有 9 个锚点、20 个类和 30 个顶点时，检测边界框和多边形的输出层的过滤器将比仅检测边界框时多 4.6 倍。另一方面，增加只发生在最后一层；所有剩余的 YOLO 层都具有相同数量的参数。从这一点来看，NN参数的总数增加了可以忽略不计的0.83%，并且处理速度不受影响。弱点在于增加在最后一层，它处理高分辨率的特征图。这会导致在训练网络时对符号张量的 VRAM 需求增加，这可能会导致学习阶段使用的最大可能批大小减少。

为了解释如何修改损失函数，我们将 Poly-YOLO 中使用的多部分损失函数描述如下：

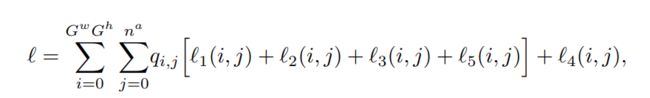
其中L1（i，j）是边界框中心预测的损失，L2（i，j）是框尺寸的损失，L3（i，j）是置信度损失，L 4(i, j) 是类预测损失，L5(i, j) 是由距离、角度和顶点置信度预测组成的边界多边形的损失。

最后，qi,j ∈ {0, 1} 是一个常数，表示第 i 个单元格和第 j 个锚点是否包含标签。

损失迭代 GwGh 网格单元和 na 锚。 部分1，. . . , 4 取自 YOLOv3 并修改为使用单个输出层的形式。 第 5 部分是新的，并通过多边形检测功能扩展了 Poly-YOLO。 在以下公式中，我们使用 b·来表示网络的预测。 损失函数的各部分定义如下：

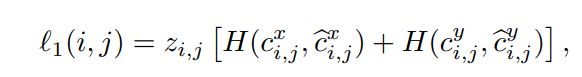
其中 cxi,j 和 cyi,j 是盒子中心的坐标，H(·,·) 是二元交叉熵，

zi,j = 2 − w*h 用于根据其宽度 wi,j 和高度 hi,j 对第 (i, j) 个框大小进行相对加权。

其中 awj 和 ahj 是第 j 个锚点的宽度和高度

其中 q^i,j 是预测的置信度，Ii,j 是一个掩码，如果 qi,j = 0 但其预测的 IoU>0.5，则排除第 i 个单元的损失部分。

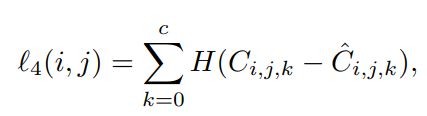
其中 Ci,j,k 是第 i 个单元格中的第 k 个类别概率。

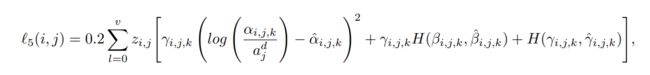
其中 adj 是第 j 个锚点的对角线。 请注意，最后一个等式是我们的多边形表示损失，这是我们的主要贡献之一。

所描述的集成方案导致同时检测边界框和边界多边形。由于协同作用，这种组合可能是有益的——卷积神经网络在其底部检测边缘，然后在中间将它们组合成更复杂的形状，并在头部 [35] 中提出高度描述性的抽象特征。因为多边形的顶点始终位于边界框内，并且顶点与边界框划定相同的对象，直觉是边界多边形部分会找到对边界框有用的特征，反之亦然。假设是带有多边形形状检测扩展的 YOLO 的训练会更​​高效并且收敛更快。该原理是众所周知的，并在文献中描述为辅助任务学习[36]。为了完整起见，让我们假设一个特殊情况，当一个对象是一个垂直的盒子。对于这种情况，边界框的轮廓将与边界多边形的轮廓重合，并且边界框和多边形都将检测到左操作顶点。尽管如此，这两种检测将是协同的，并且训练所需的时间将比普通边界框检测的训练更短。有关声明的验证，请参见第 5.3 节中带/不带边界多边形检测的 Poly-YOLO 检测结果

cites

Poly-YOLO：更快，更精确的检测和实例分割