Formal Languages and Compilers 笔记&教程 第一章 有限自动机与正则语言 (Finite Automata and Regular Languages)
Formal Languages and Compilers (形式语言和编译器) 的 自学笔记兼学习教程。
笔记作者介绍:大爽歌, b站小UP主 ,编程1对1辅导老师。
1 Finite Automata and Regular Languages
有限自动机与正则语言
In theoretical computer science and formal language theory, a regular language (also called a rational language) is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science (as opposed to many modern regular expressions engines, which are augmented with features that allow recognition of non-regular languages).
在理论计算机科学和形式语言理论中,正则语言(也称为理性语言)是一种可以由正则表达式定义的形式语言,在理论计算机科学的严格意义上(与许多现代正则表达式引擎相反, 增加了允许识别非常规语言的功能)。
Alternatively, a regular language can be defined as a language recognized by a finite automaton. The equivalence of regular expressions and finite automata is known as Kleene’s theorem (after American mathematician Stephen Cole Kleene). In the Chomsky hierarchy, regular languages are the languages generated by Type-3 grammars.
或者,可以将常规语言定义为有限自动机识别的语言。 正则表达式和有限自动机的等价性被称为 Kleene 定理(以美国数学家 Stephen Cole Kleene 命名)。 在乔姆斯基层次结构中,常规语言是由 Type-3 语法生成的语言。
1 Languages
The Formal Language Theory considers a Language as a mathematical object.
形式语言理论将语言视为数学对象。
Alphabet, string and language
字母、字符串和语言
符号与概念认识
Formal Notions:
-
symbol: 单个的基本符号
-
alphabet ∑ \sum ∑: a non-empty finite set of symbols
非空有限符号集, 一般用 ∑ \sum ∑表示 -
string over ∑ \sum ∑: a finite sequence of symbols
字母表 ∑ \sum ∑中符号的有限序列(序列:有序的排列) -
∣ w ∣ |w| ∣w∣: 获取字符串
w的长度(字符串w中符号的个数) -
ε \varepsilon ε: empty string
空字符串 -
∑ ∗ \sum^* ∑∗: the set of all strings over ∑ \sum ∑.
字母表 ∑ \sum ∑所有字符串的集合
Linguistic Universe(语言宇宙) -
language: a set of strings
字符串的一个集合(一组字符串)
关系:
L ⊆ ∑ ∗ L \subseteq \sum^* L⊆∑∗
L是 ∑ ∗ \sum^* ∑∗的一个子集
L may be infinite!
L可能是无限的
Example(举例)
- symbols: 0,1
- ∑ \sum ∑: {0, 1}
- string: 10, 01, 101, 010
- Language: {0, 011, 0111, 01111, …}
2 Deterministic Finite Automaton
Machine to recognize whether a given string is in a given set.
DFA: Deterministic Finite Automaton
确定性有限自动机
基本介绍
In DFA, for each input symbol, one can determine the state to which the machine will move.
在 DFA 中,对于每个输入符号,可以确定机器将移动到的状态。
Hence, it is called Deterministic Automaton.
因此,它被称为确定性自动机。
As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.
由于它具有有限数量的状态,因此该机器称为确定性有限机器或确定性有限自动机。
Formal Definition of a DFA
DFA 的正式定义
A deterministic finite automaton M M M is a 5-tuple ( Q Q Q, ∑ \sum ∑, δ \delta δ, q 0 q_0 q0, F F F) where
- Q Q Q: a finite set of states
一个有限集合,存放的是状态state - ∑ \sum ∑: a finite set of input symbols
一个有限集合, 存放的是输入符号(字母表) - δ \delta δ: a transition function where $\delta : Q \times \sum \rightarrow Q $
转换函数 - q 0 q_0 q0: an initial or start state $ q_0 \in Q $
初始或开始状态 - F F F: a set of accept states F ⊆ Q F\subseteq Q F⊆Q
一组接受状态(最终状态,结束状态, final state)
Graphical Representation of a DFA
A DFA is represented by digraphs called state diagram.
DFA 可由有向图表示,这样的图称为状态图。
- The vertices represent the states.
顶点代表状态。 - The arcs labeled with an input alphabet show the transitions.
标有输入字母的弧线显示了转换。 - The initial state is denoted by an empty single incoming arc.
初始状态由一个空的单个传入弧表示。 - The final state is indicated by double circles.
最终状态由双圈表示。
如果处理一串输入后, M M M的状态在 F F F中, 则该输入为可接受的(accepted)。
否则为拒绝的(rejected)
Example
举例
The following example is of a DFA M, with a binary alphabet, which requires that the input contains an even number of 0s.
以下示例是具有二进制字母表的 DFA M M M,它要求输入包含偶数个0。
M = ( Q , ∑ , δ , q 0 , F ) M = (Q, \sum, \delta, q_0, F) M=(Q,∑,δ,q0,F)
- Q = { q 0 , q 1 } Q = \{q_0, q_1\} Q={q0,q1}
- ∑ = { 0 , 1 } \sum = \{0, 1\} ∑={0,1}
- $ F = {q_0} $
转换函数 δ \delta δ如下
δ ( q 0 , 0 ) = q 1 \delta(q_0, 0) = q_1 δ(q0,0)=q1
δ ( q 0 , 1 ) = q 0 \delta(q_0, 1) = q_0 δ(q0,1)=q0
δ ( q 1 , 0 ) = q 0 \delta(q_1, 0) = q_0 δ(q1,0)=q0
δ ( q 1 , 0 ) = q 1 \delta(q_1, 0) = q_1 δ(q1,0)=q1
δ \delta δ用表格展示如下(state transition table):
| 0 | 1 | |
|---|---|---|
| q 0 q_0 q0 | q 1 q_1 q1 | q 0 q_0 q0 |
| q 1 q_1 q1 | q 0 q_0 q0 | q 1 q_1 q1 |
M M M的状态图(state diagram)如下
分析: M M M读取到0会改变状态,读取到1状态不变。
M M M只在 q 0 q_0 q0状态结束。
所以 M M M只接受偶数个0,任意个数个1。
其对应的正则表达式为(1*)(0(1*)0(1*))*。
其中*代表该字符重复任意次数(0次,1次到多次)
extended transition function
扩展转换函数
δ ^ : Q × ∑ ∗ → Q \hat \delta: Q \times \sum ^* \rightarrow Q δ^:Q×∑∗→Q
- δ ^ ( q , ε ) = q \hat \delta(q, \varepsilon)=q δ^(q,ε)=q
- δ ^ ( q , a x ) = δ ^ ( δ ( q , a ) , x ) , a ∈ ∑ , x ∈ ∑ ∗ \hat \delta(q, ax)=\hat \delta(\delta(q, a), x), a \in \sum, x \in \sum ^* δ^(q,ax)=δ^(δ(q,a),x),a∈∑,x∈∑∗
regular
正则的,正规的
- w w w is accepted by M M M if δ ^ ( q 0 , w ) ∈ F \hat \delta(q_0, w) \in F δ^(q0,w)∈F.
- w w w is rejected by M M M if δ ^ ( q 0 , w ) ∉ F \hat \delta(q_0, w) \notin F δ^(q0,w)∈/F.
- L ( M ) = { w ∈ ∑ ∗ ∣ δ ^ ( q 0 , w ) ∈ F } L(M) = \{ w \in \sum^* | \hat \delta (q_0, w) \in F\} L(M)={w∈∑∗∣δ^(q0,w)∈F} is the language acepted by M M M.
- $ A \subseteq \sum^*$ is regular if A = L ( M ) A=L(M) A=L(M) for some DFA M M M
简单来讲,如果一个语言A(A是 ∑ ∗ \sum^* ∑∗的子集),
能找到对应的DFA, 则该语言是regular.
补充
- N \Bbb N N: the set of natural numbers,
自然数集, 包含0和正整数 - A ˉ \bar{A} Aˉ: 集合 A A A的补集
- ∅ \emptyset ∅: 空集,不含任何元素,和 { ε } \{\varepsilon\} {ε}不同
3 Non-Deterministic Finite Automata
In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if
- each of its transitions is uniquely determined by its source state and input symbol, and
- reading an input symbol is required for each state transition.
在自动机理论中,有限状态机称为确定性有限自动机 (DFA),如果
-它的每个转换都由其源状态和输入符号唯一确定,并且
-每个状态转换都需要读取一个输入符号。
A nondeterministic finite automaton (NFA), or nondeterministic finite-state machine, does not need to obey these restrictions. In particular, every DFA is also an NFA. Sometimes the term NFA is used in a narrower sense, referring to an NFA that is not a DFA, but not in this article.
非确定性有限自动机 (NFA) 或非确定性有限状态机不需要遵守这些限制。 广义上,每个 DFA也是一个NFA。NFA在狭义上使用,指的是不是DFA的NFA。(后面的应该主要讨论狭义上的NFA)
简单来讲,DFA就是一个状态(state),对于每一个输入字符($ sybmol \in Q $),其结果都是唯一确定的。
如果结果不唯一有多个(或者没有),那么就是NFA
NFA也可称为NDFA, NFA可以转换为等效的DFA
Formal Definition of an NFA
A deterministic finite automaton M M M is a 5-tuple ( Q Q Q, ∑ \sum ∑, δ \delta δ, q 0 q_0 q0, F F F) where
- Q , ∑ , q 0 , F Q, \sum, q_0, F Q,∑,q0,F 和DFA中的意义相同
- transition function δ \delta δ: Q × ∑ → P ( Q ) Q \times \sum \rightarrow \mathcal P(Q) Q×∑→P(Q).
P ( Q ) \mathcal P(Q) P(Q) denotes the power set of Q Q Q, that is, the set of subsets of Q Q Q.
P ( Q ) = S ∣ S ⊆ Q \mathcal P(Q)={S | S \subseteq Q} P(Q)=S∣S⊆Q
举一个例子,来展示两者的不同。
- DFA: δ ( q 0 , a ) = q 1 \delta(q_0, a) = q_1 δ(q0,a)=q1, 其结果是单个状态
- NFA: δ ( q 0 , a ) = { q 0 , q 1 } \delta(q_0, a) = \{q_0, q_1\} δ(q0,a)={q0,q1}, 其结果是状态集合(可以是多个,甚至可以是空集)
NFA M M M 的操作基本和DFA差不多。
不同的地方如下
- If M M M is in state q q q and the next symbol is a a a then M M M moves to any state in δ ( q , a ) \delta(q, a) δ(q,a).
如果 M M M处于状态 q q q并且下一个符号是 a a a,则 M M M可以移动到 δ ( q , a ) \delta(q, a) δ(q,a)中的任何状态。 - If δ ( q , a ) \delta(q, a) δ(q,a) is empty then M M M gets stuck.
如果 δ ( q , a ) \delta(q, a) δ(q,a)为空,则 M M M会卡住。 - M accepts w if at least one transition sequence ends in a state p ∈ F after reading all of w.
在读取所有 w w w的符号后, 如果有至少一个转换序列以accpet state 结束,
即有至少一个转换序列最后状态满足 p ∈ F p \in F p∈F,则 M M M可接受 w w w。
举例理解
下面是NFA M 2 M2 M2 的图示(state diagram)
则其transition relation如下
δ ( q 0 , 0 ) = { q 0 } \delta(q_0, 0) = \{q_0\} δ(q0,0)={q0}
δ ( q 0 , 1 ) = { q 0 , q 1 } \delta(q_0, 1) = \{q_0, q_1\} δ(q0,1)={q0,q1}
δ ( q 1 , 0 ) = { q 2 } \delta(q_1, 0) = \{q_2\} δ(q1,0)={q2}
δ ( q 1 , 1 ) = { q 2 } \delta(q_1, 1) = \{q_2\} δ(q1,1)={q2}
用表格展示如下(state transition table):
| 0 | 1 | |
|---|---|---|
| q 0 q_0 q0 | { q 0 } \{q_0\} {q0} | { q 0 , q 1 } \{q_0, q_1\} {q0,q1} |
| q 1 q_1 q1 | { q 2 } \{q_2\} {q2} | { q 2 } \{q_2\} {q2} |
Possible transition sequences for input 110:
输入110时,可能的转换情况如下
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-r3nSf1k6-1657611642079)(imgs/103.png)]
其中存在一个结束状态属于 F F F
所以110能被NFA接受
NFA -> DFA
Using the subset construction algorithm, each NFA can be translated to an equivalent DFA.
使用子集构造算法,每个 NFA 都可以转换为等效的 DFA。
示例如下
把上面的NFA M 2 M2 M2 转换成 DFA
用 q 0 1 q_01 q01表示 { q 0 , q 1 } \{q_0, q_1\} {q0,q1}
则转换后的DFA表格展示如下(state transition table):
| 0 | 1 | |
|---|---|---|
| q 0 q_0 q0 | $q_0$ | q 01 q_{01} q01 |
| q 01 q_{01} q01 | q 02 q_{02} q02 | q 012 q_{012} q012 |
| q 02 q_{02} q02 | q 0 q_0 q0 | q 01 q_{01} q01 |
| q 012 q_{012} q012 | q 02 q_{02} q02 | q 012 q_{012} q012 |
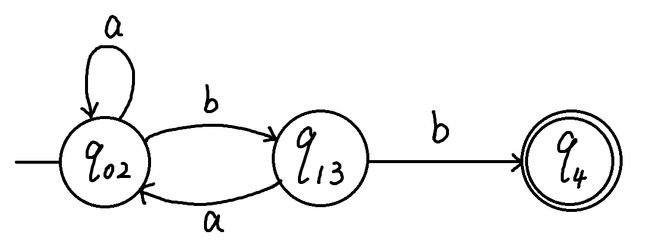
其DFA图示(state diagram)如下
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Lqsw3ygP-1657611642080)(imgs/104.png)]
ε \varepsilon ε-Transitions
Formal Definition of an NFA
A deterministic finite automaton M M M is a 5-tuple ( Q Q Q, ∑ \sum ∑, δ \delta δ, q 0 q_0 q0, F F F) where
- Q , ∑ , q 0 , F Q, \sum, q_0, F Q,∑,q0,F 和DFA中的意义相同
- ε \varepsilon ε is a speical symbol with $\varepsilon \notin \sum $
- δ : Q × ( ∑ ∪ { ε } ) → P ( Q ) \delta: Q \times (\sum \cup \{\varepsilon\} ) \rightarrow \mathcal P(Q) δ:Q×(∑∪{ε})→P(Q)
- δ \delta δ may have ε \varepsilon ε-transitions and yields a set of successor states.
QUESTION
- DFA是否每个状态都要能处理所有输入符号。
对每个输入符号,是否都要有对应箭头,没有会怎样。
回答:一定要有状态
NFA的 ε \varepsilon ε可以通过走到一个死循环节点替换。
未完待续。。。