代码随想录刷题day27 | 39. 组合总和、40.组合总和II、131.分割回文串
代码随想录刷题day27
- 39. 组合总和
- 40.组合总和II
- 131.分割回文串
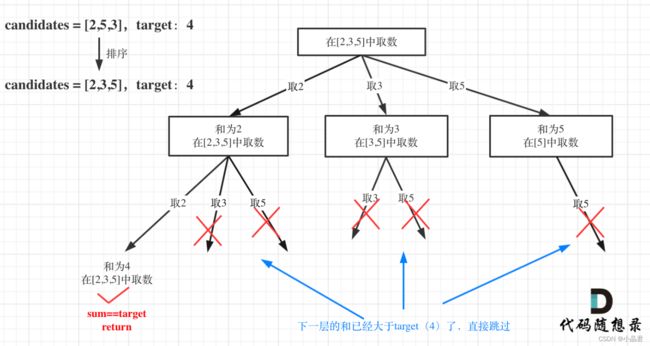
39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个数字可以无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
示例 :
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
思路:
本题的关键是同一个数字可以无限制重复被选取,所以在回溯模板里递归到下一层时,startIndex还是i
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex){
if(sum > target) return;
if(sum == target){
res.push_back(path);
return;
}
//剪枝sum + candidates[i] <= target,如果大于target就结束本轮循环
for(int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++){
path.push_back(candidates[i]);
sum += candidates[i];
backtracking(candidates, target, sum, i);//i表示可以重复读取当前的数
path.pop_back();
sum -= candidates[i];
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
sort(candidates.begin(), candidates.end());
backtracking(candidates, target, 0, 0);
return res;
}
};
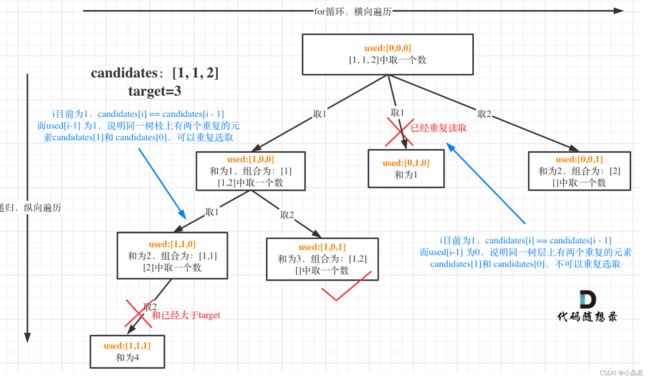
40.组合总和II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 :
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
思路:
本题给的数组中有重复的元素,要求解集中不能包含重复的组合,但是组合中的数字可以重复!
所以需要去重,其实就是使用过的元素不能重复选取,包含两个维度:树枝去重和数层去重
树枝上同一个元素不用去重,数层上同一个元素需要去重,怎样去重呢?需要一个used数组
所以去重的逻辑就是在同一层遍历时,即for循环中,如果 num[i] == num[i - 1] && used[i - 1] == false,说明已经重复读取了,就结束本次循环开始下一次循环。
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used){
if(sum == target){
res.push_back(path);
return;
}
//剪枝sum + candidates[i] <= target,如果大于target就结束本轮循环
for(int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++){
// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
// 要对同一树层使用过的元素进行跳过
if(i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false)
continue;
path.push_back(candidates[i]);
sum += candidates[i];
used[i] = true;
backtracking(candidates, target, sum, i + 1, used);
path.pop_back();
sum -= candidates[i];
used[i] = false;
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
vector<bool> used(candidates.size(), false);
sort(candidates.begin(), candidates.end());
backtracking(candidates, target, 0, 0, used);
return res;
}
};
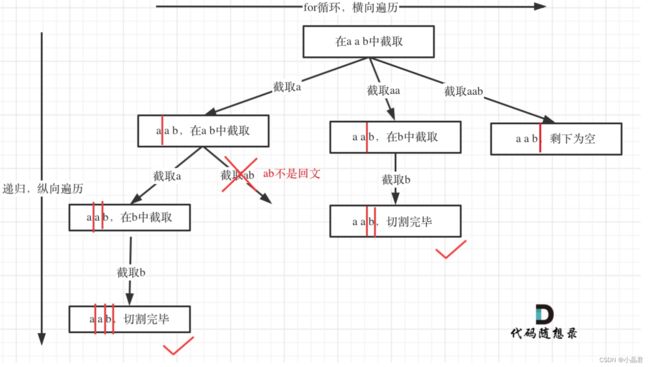
131.分割回文串
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串是正着读和反着读都一样的字符串。
示例 :
输入:s = “aab”
输出:[[“a”,“a”,“b”],[“aa”,“b”]]
class Solution {
public:
vector<string> path;
vector<vector<string>> res;
void backtracking(const string& s, int startIndex){
if(startIndex == s.size()){//当切割线到最后时,说明找到一个满足条件的结果
res.push_back(path);
return;
}
for(int i = startIndex; i < s.size(); i++){
if(isPalindrome(s, startIndex, i))
//如果是回文串,就放到path里
path.push_back(s.substr(startIndex, i - startIndex + 1));
else
continue;//否则就跳过
backtracking(s, i + 1);
path.pop_back();
}
}
//判断是否是回文串
bool isPalindrome(const string& s, int start, int end){
for(int i = start, j = end; i < j; i++, j--){
if(s[i] != s[j])
return false;
}
return true;
}
vector<vector<string>> partition(string s) {
backtracking(s, 0);
return res;
}
};