Tensor学习——创建张量及常规操作（创建、切片、索引、转换、维度变换、拼接）

Tensor学习——创建张量及常规操作（创建、切片、索引、转换、维度变换、拼接）

---

前言

近期发现卷积神经网络数据都是tensor类型的，自己浅学习了一下，总结如下。

---

一、tensor介绍

在实际使用PyTorch的过程中，张量（Tensor）对象是我们操作的基本数据类型。
  很多时候，在我们没有特别明确什么是深度学习计算框架的时候，我们可以把PyTorch简单看成是Python的深度学习第三方库，在PyTorch中定义了适用于深度学习的基本数据结构————张量，以及张量的各类计算。其实也就相当于NumPy中定义的Array和对应的科学计算方法，正是这些基本数据类型和对应的方法函数，为我们进一步在PyTorch上进行深度学习建模提供了基本对象和基本工具。因此，在正式使用PyTorch进行深度学习建模之前，我们需要熟练掌握PyTorch中张量的基本操作方法。
  当然，值得一提的是，张量的概念并非PyTorch独有，目前来看，基本上通用的深度学习框架都拥有张量这一类数据结构，但不同的深度学习框架中张量的定义和使用方法都略有差别。而张量作为数组的衍生概念，其本身的定义和使用方法和NumPy中的Array非常类似，甚至，在复现一些简单的神经网络算法场景中，我们可以直接使用NumPy中的Array来进行操作。当然，此处并不是鼓励大家使用NumPy来进行深度学习，因为毕竟NumPy中的Array只提供了很多基础功能，写简单神经网络尚可，写更加复杂的神经网络则会非常复杂，并且Array数据结构本身也不支持GPU运行，因此无法应对工业场景中复杂神经网络背后的大规模数值运算。但我们需要知道的是，工具的差异只会影响实现层的具体表现，因此，一方面，我们在学习的过程中，不妨对照NumPy中的Array来进行学习，另一方面，我们更需要透过工具的具体功能，来理解和体会背后更深层次的数学原理和算法思想。

二、Tensor（张量）创建及其类型

导入PyTorch包

import torch

torch tensor与NumPy的Array数组创建类似，许多函数是通用的。torch tensor的学习可以借鉴numpy。

1. 通过列表创建张量

t = torch.tensor([1, 2])
# 创建int16整型张量
a = torch.tensor([1.1, 2.7], dtype = torch.int16)
a,t

tensor([1, 2])
tensor([1, 2], dtype=torch.int16)

2. 通过元组创建张量

torch.tensor((1, 2))

tensor([1, 2])

3. 通过数组创建张量

import numpy as np
a = np.array((1, 2))
b = torch.tensor(a)
b

tensor([1, 2], dtype=torch.int32)

4.全0张量

torch.zeros([2, 3])   

tensor([[0., 0., 0.],
[0., 0., 0.]])

5.全1张量

torch.ones([2, 3])

6.单位矩阵

torch.eye(5)

7.对角矩阵

t = torch.tensor([1, 2])
torch.diag(t)

5.0-1均匀分布的张量

torch.rand(2, 3)

tensor([[0.5625, 0.3668, 0.7759],
[0.7236, 0.7280, 0.1522]])

8.标准正态分布的张量

torch.randn(2, 3)

tensor([[-1.2513, 0.6465, -2.3011],
[ 0.8447, 1.6856, 1.3615]])

9.指定正态分布的张量

torch.normal(2, 3, size = (2, 2))   

tensor([[2.4660, 1.4952],
[6.0202, 0.7525]])

10.整数随机采样结果

torch.randint(1, 10, [2, 4])     

tensor([[5, 8, 8, 3],
[6, 1, 4, 2]])

11.生成数列

torch.arange(5)    # 和range相同
torch.arange(1, 5, 0.5) # 从1到5（左闭右开），每隔0.5取值一个     
torch.linspace(1, 5, 3)  # 从1到5（左右都包含），等距取三个数

tensor([0, 1, 2, 3, 4])
tensor([1.0000, 1.5000, 2.0000, 2.5000, 3.0000, 3.5000, 4.0000, 4.5000])
tensor([1., 3., 5.])

12.生成未初始化的指定形状矩阵（empty）

torch.empty(2, 3)

tensor([[0.0000e+00, 1.7740e+28, 1.8754e+28],
[1.0396e-05, 1.0742e-05, 1.0187e-11]])

13.根据指定形状，填充指定数值

torch.full([2, 4], 2) 

tensor([[2, 2, 2, 2],
[2, 2, 2, 2]])

14. 创建指定形状的

t = torch.tensor([1, 2])
torch.full_like(t, 2)             # 根据t1形状，填充数值2
torch.randint_like(t, 1, 10)
torch.zeros_like(t)
#torch.randn_like(t)   #t为浮点数   

tensor([2, 2])
tensor([4, 8])
tensor([0, 0])
#tensor([1.0909, 0.0379])

三.张量类型转化

1.数据类型转化

和NumPy中array相同，当张量各元素属于不同类型时，系统会自动进行隐式转化。

数据类型	dtype
32bit浮点数	torch.float32或torch.float
64bit浮点数	torch.float64或torch.double
16bit浮点数	torch.float16或torch.half
8bit无符号整数	torch.unit8
8bit有符号整数	torch.int8
16bit有符号整数	torch.int16或torch.short
32bit有符号整数	torch.int32或torch.int
64bit有符号整数	torch.int64或torch.long
布尔型	torch.bool
复数型	torch.complex64

t = torch.tensor([1, 2])
# 转化为默认浮点型（32位）
a = t.float()
# 转化为双精度浮点型
b = t.double()
# 转化为16位整数
c = t.short()
a.dtype,b.dtype,c.dtype

(torch.float32, torch.float64, torch.int16)

2.reshape改变形状

t = torch.arange(1, 10).reshape(3, 3)
t

tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])

3.flatten拉平

t.flatten()

tensor([1, 2, 3, 4, 5, 6, 7, 8, 9])

4.张量转化为数值

n = torch.tensor(1)
n
n.item()

1

四、张量的深浅拷贝

1.浅拷贝

t = torch.arange(1, 10)
t

tensor([1, 2, 3, 4, 5, 6, 7, 8, 9])

t1 = t
t[1] = 10  
t,t1

(tensor([ 1, 10, 3, 4, 5, 6, 7, 8, 9]),
tensor([ 1, 10, 3, 4, 5, 6, 7, 8, 9]))

2.深拷贝

t = torch.arange(1, 10)
t

tensor([1, 2, 3, 4, 5, 6, 7, 8, 9])

t1 = t.clone()
t[1]=10
t,t1

(tensor([ 1, 10, 3, 4, 5, 6, 7, 8, 9]),
tensor([1, 2, 3, 4, 5, 6, 7, 8, 9]))

五、张量的索引、分片、合并以及维度调整

张量作为有序的序列，也是具备数值索引的功能，并且基本索引方法和Python原生的列表、NumPy中的数组基本一致，当然，所有不同的是，PyTorch中还定义了一种采用函数来进行索引的方式。而作为PyTorch中基本数据类型，张量即具备了列表、数组的基本功能，同时还充当着向量、矩阵、甚至是数据框等重要数据结构，因此PyTorch中也设置了非常完备的张量合并与变换的操作。

1.张量索引

#1维张量索引
t = torch.arange(1, 11)
t

tensor([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])

t[1: 8]             # 索引其中2-9号元素，并且左包含右不包含

tensor([2, 3, 4, 5, 6, 7, 8])

t1[1: 8: 2]          # 索引其中2-9号元素，左包含右不包含，且隔两个数取一个

tensor([2, 4, 6, 8])

#2维张量索引
t2 = torch.arange(1, 10).reshape(3, 3)
a = t2[0, 1]   # 表示索引第一行、第二个（第二列的）元素
b = t2[0, ::2]  # 表示索引第一行、每隔两个元素取一个
c = t2[::2, ::2]  # 表示每隔两行取一行、并且每一行中每隔两个元素取一个
a,b,c

(tensor(2),
tensor([1, 3]),
tensor([[1, 3],
[7, 9]]))

2.张量view视图

t = torch.arange(6).reshape(2, 3)
te = t.view(3, 2)   # 构建一个数据相同，但形状不同的“视图”
t,te

tensor([[0, 1, 2],
[3, 4, 5]])
tensor([[0, 1],
[2, 3],
[4, 5]])

3.张量切片

chunk函数能够按照某维度，对张量进行均匀切分，并且返回结果是原张量的视图。

t2 = torch.arange(12).reshape(4, 3)
tc = torch.chunk(t2, 4, dim=0)  # 在第零个维度上（按行），进行四等分
t2

(tensor([[0, 1, 2],
[3, 4, 5]]),
tensor([[ 6, 7, 8],
[ 9, 10, 11]]))

split既能进行均分，也能进行自定义切分。当然，需要注意的是，和chunk函数一样，split返回结果也是view。

torch.split(t2, 2, 0)           # 第二个参数只输入一个数值时表示均分，第三个参数表示切分的维度
torch.split(t2, [1, 3], 0)      # 第二个参数输入一个序列时，表示按照序列数值进行切分，也就是1/3分

(tensor([[0, 1, 2],
[3, 4, 5]]),
tensor([[ 6, 7, 8],
[ 9, 10, 11]]))

(tensor([[0, 1, 2]]),
tensor([[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]]))

4.张量合并

张量的合并操作类似与列表的追加元素，可以拼接、也可以堆叠。
cat函数

a = torch.zeros(2, 3)
b = torch.ones(2, 3)
torch.cat([a, b],0)     # 按照行进行拼接，dim默认取值为0

tensor([[0., 0., 0.],
[0., 0., 0.],
[1., 1., 1.],
[1., 1., 1.]])

堆叠函数：stack
  和拼接不同，堆叠不是将元素拆分重装，而是简单的将各参与堆叠的对象分装到一个更高维度的张量里。

a = torch.zeros(2, 3)
b = torch.ones(2, 3)
c = torch.stack([a, b])    # 堆叠之后，生成一个三维张量
c

tensor([[[0., 0., 0.],
[0., 0., 0.]],

    [[1., 1., 1.],
     [1., 1., 1.]]])

5.张量维度变换

实际操作张量进行计算时，往往需要另外进行降维和升维的操作，当我们需要除去不必要的维度时，可以使用squeeze函数，而需要手动升维时，则可采用unsqueeze函数。

t = torch.zeros(1, 1, 3, 1)
t1 = torch.squeeze(t)  #删除不必要的维度
t.shape,t1.shape

(torch.Size([1, 1, 3, 1]), torch.Size([3]))

t = torch.zeros(1, 1, 3, 1)
t1 = torch.squeeze(t,1)  #删除指定维度  维度1
t1.shape 

torch.Size([1, 3, 1])

unsqeeze函数：手动升维

t = torch.zeros(3, 1)
t1 = torch.unsqueeze(t, dim = 0)    
t1.shape   

torch.Size([1, 3, 1])

六、张量运算和广播

1.相同形状的张量计算

t = torch.arange(3)
t+t   # 对应位置元素依次相加

tensor([0, 2, 4])

标量可以和任意形状的张量进行计算，计算过程就是标量和张量的每一个元素进行计算。

t = torch.arange(3)
t+1   # 1是标量，可以看成是零维

tensor([1, 2, 3])

# 二维加零维
t = torch.arange(3)
t + torch.tensor(1)

tensor([1, 2, 3])

2.不同形状的张量计算

广播的特性是在不同形状的张量进行计算时，一个或多个张量通过隐式转化，转化成相同形状的两个张量，从而完成计算的特性。但并非任何两个不同形状的张量都可以通过广播特性进行计算，因此，我们需要了解广播的基本规则及其核心依据。

t2的形状是（1， 4），和t的形状（3， 4）在第一个分量上取值不同，但该分量上t2取值为1，因此可以广播，也就可以进行计算

t = torch.zeros(3, 4)
t2 = torch.ones(1, 4)
t + t2

tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
三维广播
两个张量的形状上有两个分量不同时，只要不同的分量仍然有一个取值为1，则仍然可以广播

t3 = torch.zeros(3, 4, 5)
t4 = torch.ones(3, 4, 1)
t3 + t4

3.逐点运算

t1 = torch.tensor([1, 2])
t2 = torch.tensor([3, 4])
torch.add(t1, t2)
#t1 + t2

tensor([4, 6])

3.1以下函数不会对原对象进行调整，而是输出新的结果。

t = torch.randn(5)
a = torch.round(t)  #取整
b = torch.abs(t) #绝对值
c = torch.neg(t)   #相反数
t,a,b,c

(tensor([ 0.2191, -1.1073, -0.8697, 0.7669, -2.8771]),
tensor([ 0., -1., -1., 1., -3.]),
tensor([0.2191, 1.1073, 0.8697, 0.7669, 2.8771]),
tensor([-0.2191, 1.1073, 0.8697, -0.7669, 2.8771]))

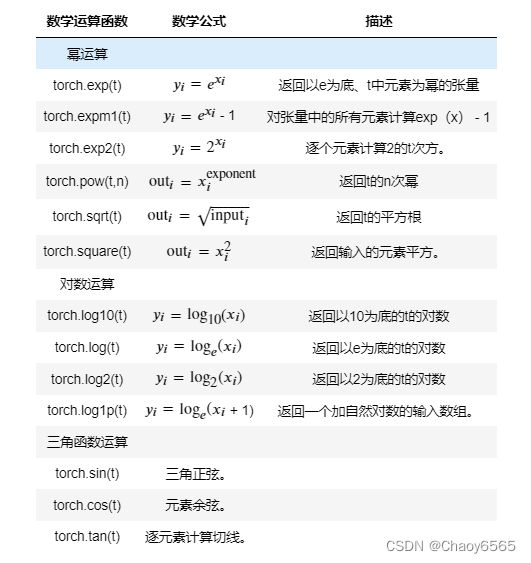
3.2要对原对象本身进行修改，则可考虑使用方法_()的表达形式，对对象本身进行修改。此时方法就是上述同名函数。

t = torch.randn(5)
t.abs_()
t.neg_()
t.exp_()
torch.pow(t, 2)  # 计算t的2次方
torch.square(t)
torch.log10(t)
# 这里结果太多就不进行展示了

4.规约运算

以下函数很简单就不进行演示了

函数	描述
torch.mean(t)	返回张量均值
torch.var(t)	返回张量方差
torch.std(t)	返回张量标准差
torch.var_mean(t)	返回张量方差和均值
torch.std_mean(t)	返回张量标准差和均值
torch.max(t)	返回张量最大值
torch.argmax(t)	返回张量最大值索引
torch.min(t)	返回张量最小值
torch.argmin(t)	返回张量最小值索引
torch.median(t)	返回张量中位数
torch.sum(t)	返回张量求和结果
torch.logsumexp(t)	返回张量各元素求和结果，适用于数据量较小的情况
torch.prod(t)	返回张量累乘结果
torch.dist(t1, t2)	计算两个张量的闵式距离，可使用不同范式
torch.topk(t)	返回t中最大的k个值对应的指标

t1 = torch.tensor([1.0, 2])
t2 = torch.tensor([3.0, 4])
a = torch.dist(t1, t2, 1)  #p取值为1时，计算接到距离
b = torch.dist(t1, t2, 2)  #p取值为2时，计算欧式距离
a,b

(tensor(4.), tensor(2.8284))

# 按照第一个维度求和（每次计算三个）、按列求和
t2 = torch.arange(12).float().reshape(3, 4)
torch.sum(t2, dim = 0)

tensor([12., 15., 18., 21.])

torch.sort(t) # 升序排列
torch.sort(t, descending=True)# 降序排列
# 修改dim和descending参数，使得按列进行降序排序
torch.sort(t, dim = 0, descending=True)

5.比较运算

函数	描述
torch.eq(t1, t2)	比较t1、t2各元素是否相等，等效==
torch.equal(t1, t2)	判断两个张量是否是相同的张量
torch.gt(t1, t2)	比较t1各元素是否大于t2各元素，等效>
torch.lt(t1, t2)	比较t1各元素是否小于t2各元素，等效<
torch.ge(t1, t2)	比较t1各元素是否大于或等于t2各元素，等效>=
torch.le(t1, t2)	比较t1各元素是否小于等于t2各元素，等效<=
torch.ne(t1, t2)	比较t1、t2各元素是否不相同，等效!=

t1 = torch.tensor([1.0, 3, 4])
t2 = torch.tensor([1.0, 2, 5])
t1 == t2

tensor([ True, False, False])

torch.equal(t1, t2)          # 判断t1、t2是否是相同的张量

False

torch.eq(t1, t2)

tensor([ True, False, False])

t1 > t2

tensor([False, True, False])

t1 >= t2

tensor([ True, True, False])

总结

未完待续，，，