Logistic Regression逻辑回归函数Python实现

*逻辑回归（Logistic Regression）*是一种分类算法。不同于线性回归的回归属性，逻辑回归是的输出是一组离散值。以最简单的二元分类为例，逻辑回归通过每个样本的特征和其相应权重的相乘之后，通过sigmoid函数来得到相应的（0，1）值。如上所述，逻辑回归的预测函数为$$g(x)=\frac{1}{1+e^{-z}}$$，其中$$z=W^{T}X$$，W,X分别为我们要求的权重和特征向量。之所以用Sigmoid函数是因为Sigmoid函数良好的性质，如图

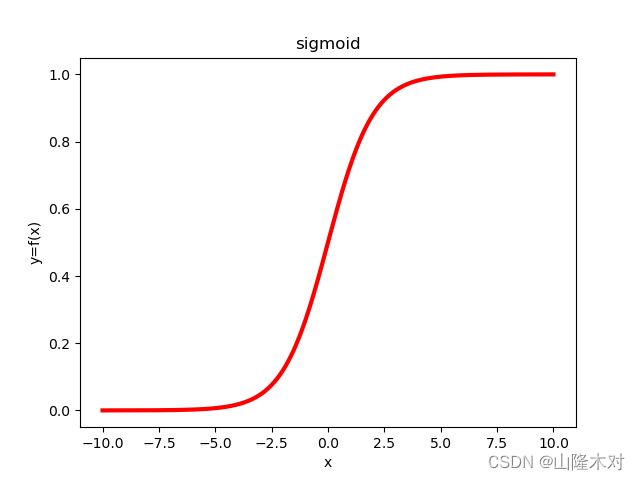
因为Sigmoid函数可以将（-∞，+∞）上的值映射到（0，1）区间，因此，Sigmoid输出也可以表示一种概率，即，$$p(y=1|W,X)=\frac{1}{1+e^{-W^{T}X}}$$,$$p(y=0|W,X)=1-p(y=1|W,X)$$。

所以对一个样本预测正确的概率为$$p(right)=p(y=1{)}^{y_i}\ast p(y=0{)}^{1-y_i}$$。
我们希望这个预测的正确率达到最大，可以用极大似然函数来进行求解。即
$$ln(L(\theta ))=\sum _{i=1}^m{y}_{i}ln(g({\theta }^{T}X))+(1-y_i)ln(1-g({\theta }^{T}X))$$我们期望对每个样本的估计值的正确率都能够达到最大，即对极大似然函数求其极大值。其间，在函数值优化过程中，我们习惯用最小化，因此在极大似然函数前面加一个负号.

根据西瓜书所说（证明），上述函数是凸函数，因此可以用牛顿法或者梯度下降法对齐进行求解。
因此，即为我们所求的目标函数。为求其最（极）小值，对其求梯度。
$$\frac{\partial J}{\partial \theta }=-\sum _{i=1}^m(y_i-g({\theta }^T{X}_i))X_i$$
(敲公式太麻烦，直接给结果了)
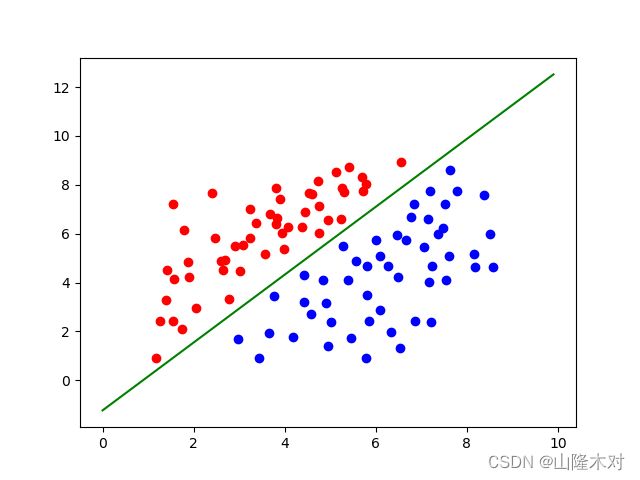
笔者使用直球梯度下降法对数据集进行求解。所选用的数据集为线性分布的二维样本点，并且其标签为（0，1）二元值。

数据处理

data=pd.read_csv("data1.csv",header=None)
data=data.values
labels=data[:,-1]
labels=(labels+1)/2
feature=data[:,:-1]

len=feature.shape[0]

要是有人看，需要数据集的话就留个言吧

梯度下降

注意这里将梯度下降的过程分解一下，方便debug，然后毕竟数据量少，就用最原始的梯度下降法了，不搞那些奇淫巧技了

#梯度下降算法
def GDescent(train_data,train_label,coeffience,alpha=0.1):
    m=train_data.shape[0]
    if(m==train_label.shape[0]):
        # step1=np.multiply(train_label,train_data.T)/(1+np.exp(np.dot(coeffience,train_data.T)))
        # step2=-np.multiply(1-train_label,train_data.T)
        # step3=np.exp(-2*np.dot(coeffience,train_data.T))+np.exp(-np.dot(coeffience,train_data.T))
        # step4=step2/step3   #这里是之前自己推导的梯度，然后有点问题
        step1=1/(1+np.exp(-np.dot(coeffience,train_data.T)))
        step2=step1-train_label
        step3=np.multiply(step2,train_data.T).T
        step4=np.sum(step3,axis=0)/m
        differential_array=step4

        differential_array=differential_array.T
        # differential=np.sum(differential_array,axis=0)/m

        coeffience=coeffience-alpha*differential_array

        return coeffience
    pass

预测函数

def PreCal(train_data,coeffience):
    test_pre=1/(1+np.exp(-np.dot(coeffience,train_data.T)))
    # test_pre=(np.exp(test_pre)-np.exp(-test_pre))/(np.exp(test_pre)+np.exp(test_pre))
    return test_pre

误差求解

def DistanceCal(test_pre,train_label):
    m=test_pre.shape[0]
    if(m==train_label.shape[0]):
        distance=np.sum(np.abs(test_pre-train_label)/m)
        return distance

初始化参数及求解

因为数据集是线性可分的，且

feature_dim=feature.shape[1]
coeffience=np.ones(feature_dim)
distance_e=1e-3
test_pre=np.zeros(labels.shape[0])
distance=DistanceCal(test_pre,labels)
coeffiences=[]
start=time()
while(distance>distance_e):
    coeffiences.append(coeffience)
    coeffience=GDescent(feature,labels,coeffience)
    test_pre=PreCal(feature,coeffience)
    distance=DistanceCal(test_pre,labels)
    print("The current coeffience is ",coeffience)
    print("The current distance is ",distance)
print("The cost time is ",time()-start)
print("The best codffiences is :",coeffiences[-1])
print("The smallest distance is :",distance)

画图

data_plus_x=[]     #正样例
data_plus_y=[]     #正样例
data_minus_x=[]    #负样例
data_minus_y=[]    #负样例

for i in range(data.shape[0]):
    if data[i][-1]==1:
        data_plus_x.append(data[i][1])
        data_plus_y.append(data[i][2])
    if data[i][-1]==-1:
        data_minus_x.append(data[i][1])
        data_minus_y.append(data[i][2])

pyplot.scatter(data_plus_x,data_plus_y,c="r")
pyplot.scatter(data_minus_x,data_minus_y,c="b")
x=np.arange(0,10,0.1)
y=(-coeffience[0]-coeffience[1]*x)/coeffience[2]
pyplot.plot(x,y,c="g")
pyplot.show()

结果和图

GPU版本

之后，早就听说一种可以使用GPU的掌法，遂想试一试，使用的是numba的cuda库，对于没有cuda C++编程经验的人来讲，接口也相对比较简单，容易上手。CudaAPI。
和CPU处理不同，GPU主要做一些大量的并行简单运算，因此，需要先为执行的数据分配GPU，并且指定其中的Grid、Block、Thread数量。直接上代码

from numba import cuda
import pandas as pd
from math import exp,fabs,ceil
import numpy as np
from time import time
from matplotlib import pyplot
data=pd.read_csv("data1.csv",header=None)
data=data.values
labels=data[:,-1]
labels=(labels+1)/2     #将（1，-1）映射到（1，0）
features=data[:,:-1]
distance_e=1e-3     #预测值和真实值的绝对值误差
result=cuda.device_array([features.shape[0],features.shape[1]])   #用于保存各个点的梯度
test_pre_gpu=cuda.device_array(labels.shape[0])      #用于保存预测值
distances_gpu=cuda.device_array(labels.shape[0])     #用于保存预测值和真实值的误差
thread_per_block_2D=(16,16)
block_per_grid_x=ceil(features.shape[0]/thread_per_block_2D[0])
block_per_grid_y=ceil(features.shape[1]/thread_per_block_2D[1])
block_per_grid_2D=(block_per_grid_x,block_per_grid_y)
thread_per_block=128
block_per_grid=ceil(features.shape[0]*features.shape[1]/thread_per_block)
m=features.shape[0]   #数据量


#梯度下降
@cuda.jit()
def GDescent(train_data,train_label,coeffience,result):
    # idx=cuda.threadIdx.x+cuda.blockIdx.x*cuda.blockDim.x
    # idy=cuda.threadIdx.y+cuda.blockIdx.y*cuda.blockDim.y
    idx,idy=cuda.grid(2)
    if idx<train_data.shape[0] and idy <train_data.shape[1]:
        tmp=0
        for i in range(coeffience.shape[0]):
            tmp+=-coeffience[i]*train_data[idx][i]

        result[idx][idy]=(1/(1+exp(tmp))-train_label[idx])*train_data[idx][idy]


@cuda.jit()
def PreCal(train_data,coeffience,test_pre):
    idx=cuda.threadIdx.x+cuda.blockIdx.x*cuda.blockDim.x
    idy=cuda.threadIdx.y+cuda.blockIdx.y*cuda.blockDim.y
    if idx<train_data.shape[0] and idy<train_data.shape[1]:
        tmp=0
        for i in range(coeffience.shape[0]):
            tmp+=-coeffience[i]*train_data[idx][i]
        test_pre[idx]=1/(1+exp(tmp))

@cuda.jit()
def DistanceCal(test_pre,train_label,distances):
    idx=cuda.threadIdx.x+cuda.blockIdx.x*cuda.blockDim.x
    if idx<test_pre.shape[0]:
        distances[idx]=fabs(test_pre[idx]-train_label[idx])

coeffiences=[]
distance=1
coeffience=np.ones(features.shape[1])
test_pre=0
alpha=0.1

start=time()
while(distance>distance_e):
    coeffiences.append(coeffience)
    GDescent[block_per_grid_2D, thread_per_block_2D](features, labels, coeffience, result)
    cuda.synchronize()
    gradient = np.sum(result.copy_to_host(), axis=0) / m
    coeffience=coeffience-alpha*gradient
    PreCal[block_per_grid,thread_per_block](features,coeffience,test_pre_gpu)
    cuda.synchronize()
    test_pre=test_pre_gpu.copy_to_host()
    DistanceCal[block_per_grid,thread_per_block](test_pre,labels,distances_gpu)
    cuda.synchronize()
    distances=distances_gpu.copy_to_host()
    distance=np.sum(distances)/m
    print("The current coeffience is ",coeffience)
    print("The current distance is ",distance)
print("The GPU cost time is",time()-start)

print("The best coeffience is :",coeffiences[-1])
print("The smallest distance is :",distance)

data_plus_x=[]     #正样例
data_plus_y=[]     #正样例
data_minus_x=[]    #负样例
data_minus_y=[]    #负样例

for i in range(data.shape[0]):
    if data[i][-1]==1:
        data_plus_x.append(data[i][1])
        data_plus_y.append(data[i][2])
    if data[i][-1]==-1:
        data_minus_x.append(data[i][1])
        data_minus_y.append(data[i][2])

pyplot.scatter(data_plus_x,data_plus_y,c="r")
pyplot.scatter(data_minus_x,data_minus_y,c="b")
x=np.arange(0,10,0.1)
y=(-coeffience[0]-coeffience[1]*x)/coeffience[2]
pyplot.plot(x,y,c="g")
pyplot.show()

最后结果如下


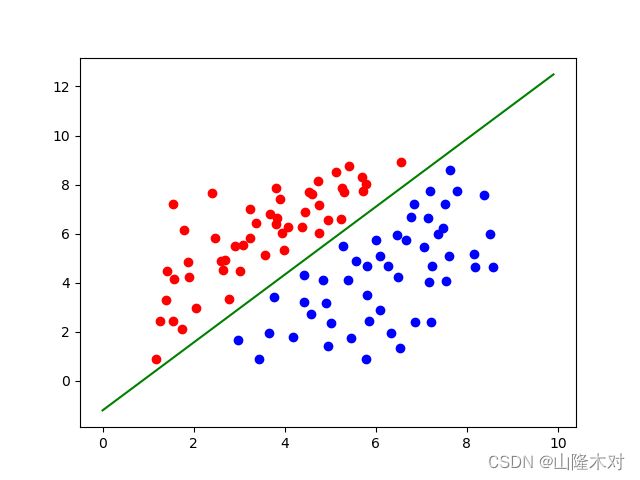
可以看到最后求出的权重和CPU版本是一样的，但是时间远不如想象中的理想，原因如下：
1）在CPU版本中，使用了Numpy库，numpy在底层性能上已经可以说是优化到极致了。
2）使用GPU计算的逻辑是，由于GPU的memory比较小，因此需要将数据先从CPU拷贝到GPU，计算之后再将结果返回，因此会产生通信代价。
但是我看过其他博主写过的文章里用numba.cuda处理1200W数据量的样本时，花费的时间确实要比CPU要小很多。也就是当数据量达到一定规模时，GPU计算的优势才能够得以体现。