关于卷积神经网络CNN

卷积神经网络

卷积操作：

        卷积核和扫过的区域对应位置相乘再求和的操作，卷积完成后一般要加个偏置bias。一种Kernel如果分成多个通道上的子Kernel做卷积运算，最后运算结果还要加在一起后，再加偏置 

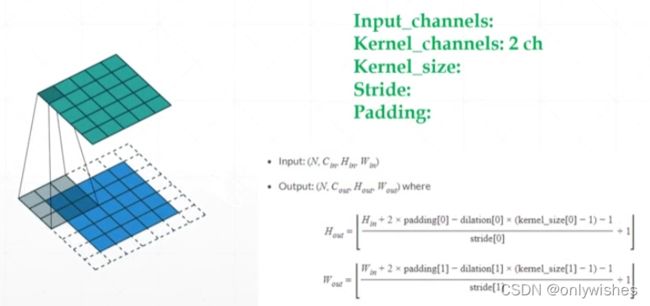
input_channels:输入的通道

kernel_channels:有几个卷积核

kernel_size:卷积核的大小

stride:卷积核移动的步长

padding：打补丁，1就是1层

---

multi-kernels

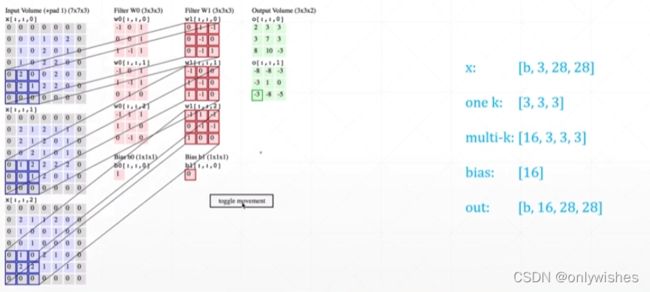
多kernel情况参数理解

x: b张照片，每张3个通道，大小28*28

onek：一个核的通道与照片是一样的，大小任意选

multi-k：核的数量，核的通道，大小

bias：每个核都有一个偏置，有多少核就有多少偏置

out：输入多少张就输出多少张，有多少个核就多少通道，最后大小根据情况输出

---

nn.Conv2d

二维卷积可以处理二维数据

nn.Conv2d( in_channels, out_channels,kernels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True))
参数：
  in_channel:　输入数据的通道数，例RGB图片通道数为3；
  out_channel: 输出数据的通道数，这个根据模型调整；
  kennel_size: 卷积核大小，可以是int，或tuple；kennel_size=2,意味着卷积大小(2,2)， kennel_size=（2,3），意味着卷积大小（2，3）即非正方形卷积
  stride：步长，默认为1，与kennel_size类似，stride=2,意味着步长上下左右扫描皆为2， stride=（2,3），左右扫描步长为2，上下为3；
  padding：　周围使用零填充

cove1d：用于文本数据，只对宽度进行卷积，对高度不进行卷积 cove2d：用于图像数据，对宽度和高度都进行卷积

import torch
import torch.nn as nn
layer = nn.Conv2d(1,3,kernel_size=3,stride=1,padding=0)     #卷积层
x = torch.rand(1,1,28,28)    #样本数=1，通道数=1，
out = layer.forward(x)  #   向前传播
print(out.size())    #3个核3个通道

layer = nn.Conv2d(1,3,kernel_size=3,stride=2,padding=1)
out = layer.forward(x)
print(out.size())

out = layer(x)      #__call__魔法，先运行hooks再运行.forward()函数.实际使用方法
print(out.size())

torch.Size([1, 3, 26, 26])
torch.Size([1, 3, 14, 14])
torch.Size([1, 3, 14, 14])

---

inner weight & bias

inner_layer是一个卷积层，卷积层中所包含的参数由两个部分，一是卷积核权重矩阵weight，二是卷积核的偏置bias。因此，输出有layer2.layer_inner.weight和layer2.layer_inner.bias

layer = nn.Conv2d(1,3,kernel_size=3,stride=2,padding=1)
w = layer.weight
print(w)        #一个核三个通道的权重
print(layer.weight.shape)
print(layer.bias.shape) #一个核几个通道几个偏置

Parameter containing:
tensor([[[[-0.2343,  0.1892,  0.2940],        #每个通道的权重
          [ 0.0495,  0.1050,  0.1973],
          [ 0.3005, -0.2877,  0.0205]]],


        [[[ 0.1760, -0.1302,  0.2827],
          [-0.0858, -0.0841, -0.2342],
          [ 0.1552, -0.1263, -0.2716]]],


        [[[-0.1086,  0.1004, -0.2107],
          [-0.0503,  0.2460, -0.0588],
          [ 0.0419,  0.2345,  0.1198]]]], requires_grad=True)
torch.Size([3, 1, 3, 3])        
torch.Size([3])        #3通3偏置

---

F.conv2d

nn.Conv2d是[2D卷积层]，而F.conv2d是[2D卷积操作]

import torch
from torch.nn import functional as F
'''手动定义卷积核（weight）和偏置'''
w = torch.rand(16,3,5,5)    #16种3通道的5*5卷积核
b = torch.rand(16)  #和卷积核种类数一致

'''定义输入样本'''
x = torch.randn(1,3,28,28)  #1张3通道的28*28的图像

'''2D卷积输出'''
out = F.conv2d(x,w,b,stride=1,padding=1)    #步长为1，加一圈0
print(out.shape)

out = F.conv2d(x,w,b,stride=2,padding=2)
print(out.shape)

torch.Size([1, 16, 26, 26])
torch.Size([1, 16, 14, 14])

---

池化层与采样

 pooling下采样

分为maxpooling 和avgpooling,

 池化层在卷积神经网络中的作用在于特征融合和降维。池化也是一种类似的卷积操作，

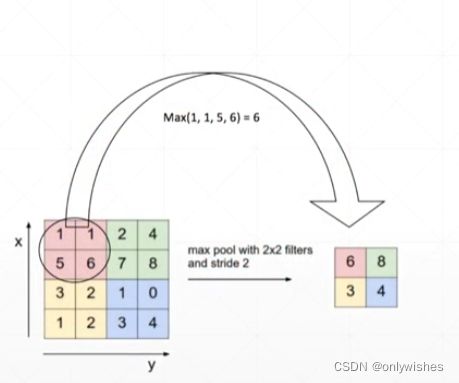
maxpooing 就是一个核在数据上滑动，取最大值输出

class torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)

maxpooling有局部不变性而且可以提取显著特征的同时降低模型的参数，从而降低模型的过拟合。

avgpooling 就是取平均值输出，输出大小都由步长影响

import torch
from torch.nn import functional as F
import torch.nn as nn
x = torch.randn(1,16,14,14)
'''从nn中导入最大池化'''
layer = nn.MaxPool2d(2,stride=2)    #步长2
out = layer(x)
print(out.shape)

'''使用F.方式平均池化'''
out = F.avg_pool2d(x,2,stride=2)
print(out.shape)

torch.Size([1, 16, 7, 7])
torch.Size([1, 16, 7, 7])

---

upsample上采样

使用torch.nn.functional.interpolate( input, size, scale_factor , mode)

        imput：输入的tensor

        size：输出的大小

        scal_factor（float or turtle[float]）：缩放因子，如果是turtle,要与输入的大小相匹配

        mode （str）: 上采样所用的算法，默认'nearest'

x = out         #torch.Size([1, 16, 7, 7])
out = F.interpolate(x,scale_factor=2,mode='nearest')    #采用最近邻采样
print(out.shape)        #torch.Size([1, 16, 14, 14])

out = F.interpolate(x,scale_factor=3,mode='nearest')
print(out.shape)        #torch.Size([1, 16, 21, 21])

---

Relu激活函数

 把图片中负的单元去掉

x = torch.randn(1,16,7,7)
'''采用nn.'''
layer = nn.ReLU(inplace=True)   #True直接替代
out = layer(x)
print(out.shape)    #torch.Size([1, 16, 7, 7])

'''采用F.'''
out = F.relu(x)
print(out.shape)    #torch.Size([1, 16, 7, 7])

---

BatchNorm

 说明：

归一化就是要把需要处理的数据经过处理后（通过某种算法）限制在你需要的一定范围内。

首先归一化是为了后面数据处理的方便，其次是保证程序运行时收敛加快。归一化的具体作用是归纳统一样本的统计分布性。归一化在0-1之间是统计的概率分布

归一化的目的是使得没有可比性的数据变得具有可比性，同时又保持相比较的两个数据之间的相对关系，如大小关系或是为了作图方便，原来很难在一张图上作出来的图形，归一化后就可以很方便的显示出在图上的相对位置等。

标准化是处理后的数据服从N (0,1) 的正态分布。

在模型训练时，批量归一化利用小批量上的均值和标准差，不断调整神经网络的中间输出，从而使整个神经网络在各层的中间输出的数值更稳定

批量标准化的优点

        可以使用更大的学习率，也更稳定

        加速模型收敛，可以不用精心设计权值初始化

        可以不用 dropout 或者较小的 dropout

---

batchnorm1d用于全连接层

nn.batchnorm( input)

        input:输入的feature数量

x = torch.randn(100,16)+0.5            #x~N(0.5,1)
layer = torch.nn.BatchNorm1d(16)
print(layer.running_mean)       #初始化均值
print(layer.running_var)        #初始化方差
out = layer(x)

print(layer.running_mean)       #批量标准化后均值
print(layer.running_var)        #方差

tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
tensor([0.0786, 0.0445, 0.0536, 0.0518, 0.0595, 0.0333, 0.0502, 0.0462, 0.0501,
        0.0340, 0.0538, 0.0316, 0.0502, 0.0352, 0.0536, 0.0548])
tensor([0.9851, 0.9965, 0.9842, 0.9728, 0.9911, 1.0073, 0.9874, 1.0043, 0.9916,
        0.9965, 0.9855, 0.9888, 0.9916, 0.9754, 0.9910, 0.9911])

这里barch均值真实0.5，

barchnorm1d会慢慢更新u 来接近它真实的均值和方差而不是一次到位。

u' = (1-m)u + m*ut

u'为更新值，u为当前均值，初始化时为0，m的值在barchnorm1d中设置，不输入的话默认o.1，ut 为当前barch的均值

---

x = torch.randn(100,16)+0.5
layer = torch.nn.BatchNorm1d(16)
for i in range(100):
    out = layer(x)            #每一次循环layer里面的值都改变，不是初始化的值，由上一次得出下一次
print(layer.running_mean)       #100次就很接近ut的真实值了
print(layer.running_var)        #方差

tensor([0.3660, 0.4934, 0.6168, 0.5528, 0.6549, 0.4958, 0.3614, 0.5894, 0.6229,
        0.3940, 0.5559, 0.5998, 0.5506, 0.5580, 0.4186, 0.5184])    #大部分接近0.5了

tensor([1.0823, 0.9604, 0.8071, 0.9483, 0.8612, 0.9657, 1.0367, 1.1214, 1.1335,
        1.2873, 1.0255, 0.6689, 1.1824, 0.8369, 1.0292, 0.9861])    #接近

---

batchnorm2d用于卷积层

x = torch.rand(1,16,7,7)
layer = nn.BatchNorm2d(16)    #必须与上面的值相等，
out = layer(x)
print(out.shape)

print(layer.weight)        #这里的weight相当于γ
print(layer.weight.shape)   #
print(layer.bias.shape)     #相当于β

---

class variables 

打印输出所有的类

x = torch.rand(1,16,7,7)
layer = nn.BatchNorm2d(16)
out = layer(x)
print(vars(layer))

{
'training': True,     ##表是当前状态
'_parameters': OrderedDict([('weight', Parameter containing:
tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
       requires_grad=True)), ('bias', Parameter containing:
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       requires_grad=True))]),
'_buffers': OrderedDict([('running_mean', tensor([0.0534, 0.0456, 0.0509, 0.0522, 0.0455, 0.0464, 0.0489, 0.0455, 0.0587,
        0.0477, 0.0530, 0.0576, 0.0459, 0.0435, 0.0512, 0.0524])), ('running_var', tensor([0.9089, 0.9075, 0.9086, 0.9084, 0.9083, 0.9068, 0.9081, 0.9083, 0.9095,
        0.9071, 0.9082, 0.9095, 0.9064, 0.9082, 0.9091, 0.9074])), ('num_batches_tracked', tensor(1))]), 
'_non_persistent_buffers_set': set(), 
'_backward_hooks': OrderedDict(), 
'_is_full_backward_hook': None, 
'_forward_hooks': OrderedDict(), 
'_forward_pre_hooks': OrderedDict(), 
'_state_dict_hooks': OrderedDict(), 
'_load_state_dict_pre_hooks': OrderedDict(), 
'_modules': OrderedDict(), 
'num_features': 16, 
'eps': 1e-05, 
'momentum': 0.1, 
'affine': True,         ##表示β和γ需要自动学习
'track_running_stats': True
}

---

test 

在test时u和方差没法更新，使用全局的running 不需要β和γ

因此要加入以下一行代码 

layer.eval()

---

nn.module

 1、包含所有常用方法

比如nn.Linear、nn.BatchNorm2d、nn.Conv2d等等都继承于nn.module。并且还可以嵌套使用

所有其他网络都是这个类的继承。我们在自己定义一个网络或者层时，就需要继承这个类。module允许以树结构进行嵌入，一个module可以包含其他module，这个module就是原有module的submodule

---

2、使用nn.Sequential()容器

nn.Module中的和自己写的都可以在这里使用

classNet中首先通过super函数继承torch.nn.Module模块的构造方法，再通过添加属性的方式搭建神经网络各层的结构信息，在forward方法中完善神经网络各层之间的连接信息，然后再通过定义Net类对象的方式完成对神经网络结构的构建.

 自定义层时必须要继承nn.Module，并且在其构造函数中需要调用nn.Module的构造函数

快速构建方法，就是通过torch.nn.Sequential，直接完成对神经网络的建立。

import torch.nn as nn
net = nn.Sequential(
    nn.Conv2d(1,32,5,1,1),
    nn.MaxPool2d(2,2),
    nn.ReLU(True),
    nn.BatchNorm2d(32),

    nn.Conv2d(32,64,3,1,1),
    nn.ReLU(True),
    nn.BatchNorm2d(64),

    nn.Conv2d(64,64,3,1,1),
    nn.MaxPool2d(2,2),
    nn.ReLU(True),
    nn.BatchNorm2d(64),

    nn.Conv2d(64,128,3,1,1),
    nn.ReLU(True),
    nn.BatchNorm2d(128)
)
print(net)

Sequential(
  (0): Conv2d(1, 32, kernel_size=(5, 5), stride=(1, 1), padding=(1, 1))
  (1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (2): ReLU(inplace=True)
  (3): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (4): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (5): ReLU(inplace=True)
  (6): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (7): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (8): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (9): ReLU(inplace=True)
  (10): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (11): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (12): ReLU(inplace=True)
  (13): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)

---

3、nn.Module可以自动管理parameters

对于Sequential实例中含模型参数的层，我们可以通过Module类的parameters()或者named_parameters方法来访问所有参数（以迭代器的形式返回），后者除了返回参数Tensor外还会返回其名字

直接输出网络的参数是无法输出出来的,需要调用list将其输出

net = nn.Sequential(nn.Linear(4,2),nn.Linear(2,2))
print(list(net.parameters())[0].shape)  #第0层的weight，由于w输入和输出位置相反所以反着
print(list(net.parameters())[3].shape)  #第1层的偏置

print(list(net.named_parameters())[0])  #带名字
print(list(net.named_parameters())[1])

print(dict(net.named_parameters()).items()) #字典形式返回参数信息

torch.Size([2, 4])
torch.Size([2])

('0.weight', Parameter containing:
tensor([[-0.1850, -0.3564, -0.0868,  0.2885],
        [ 0.4072,  0.4144,  0.3386,  0.0323]], requires_grad=True))
('0.bias', Parameter containing:
tensor([-0.4205, -0.1766], requires_grad=True))

dict_items([('0.weight', Parameter containing:
tensor([[-0.1850, -0.3564, -0.0868,  0.2885],
        [ 0.4072,  0.4144,  0.3386,  0.0323]], requires_grad=True)),
 ('0.bias', Parameter containing:
tensor([-0.4205, -0.1766], requires_grad=True)), 
('1.weight', Parameter containing:
tensor([[ 0.6508, -0.4416],
        [ 0.2194, -0.5437]], requires_grad=True)),
('1.bias', Parameter containing:
tensor([-0.3002, -0.2581], requires_grad=True))])

 因此可以把这些用parameters直接传到优化器中

optimizer = optim.SGD(net.parameters(),lr=1e-3)

---

4、modules

modules：所有的结点，

children：直系亲属，儿子女儿

class BasicNet(nn.Module):
    def __init__(self):
        super(BasicNet, self).__init__()
        self.net = nn.Linear(4, 3)
    def forward(self, x):
        return self.net(x)
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.net = nn.Sequential(BasicNet(),
                                 nn.ReLU(),
                                 nn.Linear(3, 2))
    def forward(self, x):
        return self.net(x)

net = Net()
#print(list(net.named_children()))
#print(list(net.named_modules()))

for m in net.named_children():    # 打印直系亲属
    print('children:',  m)
for m in net.named_modules():        #所有结点
    print('modules:',  m)

children: ('net', Sequential(        #只有一个直系sequential,里面包含3个，其中BasicNet又包一个
  (0): BasicNet(
    (net): Linear(in_features=4, out_features=3, bias=True)
  )
  (1): ReLU()
  (2): Linear(in_features=3, out_features=2, bias=True)
))
modules: ('', Net(        #根节点，包含本身共有6个结点
  (net): Sequential(        
    (0): BasicNet(           
      (net): Linear(in_features=4, out_features=3, bias=True)    
    )
    (1): ReLU()        
    (2): Linear(in_features=3, out_features=2, bias=True)    
  )
))
modules: ('net', Sequential(        #次根，5个节点
  (0): BasicNet(
    (net): Linear(in_features=4, out_features=3, bias=True)
  )
  (1): ReLU()
  (2): Linear(in_features=3, out_features=2, bias=True)
))
modules: ('net.0', BasicNet(        #2个
  (net): Linear(in_features=4, out_features=3, bias=True)
))
modules: ('net.0.net', Linear(in_features=4, out_features=3, bias=True))    #1
modules: ('net.1', ReLU())                                                #1
modules: ('net.2', Linear(in_features=3, out_features=2, bias=True))        #1

---

 5、to(device)

在什么设备上使用

device = torch.device('cuda')
net = Net()
net.to(device)    #.to()会返回net引用和原来一样，但是tensor不一样

---

6、save and load

在训练时时间可能会很久，为防止意外，要隔一段时间保存一下数据，

state_dict()会返回当前训练的状态，save ()会将其保存到文件里

若之前意外停止，重新开始时 先使用 load()将上次保存的加载为pytorch类，在加载到module里面去，里面的值初始化为上次训练好的值。不需要重新初始化

net.load_state_dict(torch.load('ckpt.mdl'))    #开始时加载模型 
#train
torch.save(net.state_dict(),'ckpt.mdl')    

---

7、train / test

不同的类训练测试方法可能不一样，因此

使用nn.traini()就切换到训练模式

使用nn.eval()就切换到测试模式

    # train
    net.train()
    ...
    # test
    net.eval()
    ...

---

8、实现我们自己的类

class MyLinear(nn.Module):
    def __init__(self, inp, outp):      #w[outp,inp]
        super(MyLinear, self).__init__()
        # requires_grad = True
        self.w = nn.Parameter(torch.randn(outp, inp))    # nn.Parameter会自动地将torch.tensor通过nn.Parameter加到nn.parameter()里面去
        self.b = nn.Parameter(torch.randn(outp))
        
    def forward(self, x):
        x = x @ self.w.t() + self.b
        return x

这个和Linear是完全一样的

这里使用Parameter会自动设置参数需要读信息，并且会将其送到parameter里可以使用优化器，tensor无法直接使用

---

 实现一个打平的类，可以直接用

class Flatten(nn.Module):  # 定义将所有的打平，在sequential里面一次forward就行
    def __init__(self):
        super(Flatten, self).__init__()
    def forward(self, input):                   #二维才能送到线性层因此要打平
        return input.view(input.size(0), -1)  # -1表示将其他所有的打平

class TestNet(nn.Module):
    def __init__(self):
        super(TestNet, self).__init__()
        self.net = nn.Sequential(nn.Conv2d(1, 16, stride=1, padding=1),
                                 nn.MaxPool2d(2, 2),
                                 Flatten(),  # 实现自己的类，里面只能写类
                                 nn.Linear(1 * 14 * 14, 10))
    def forward(self, x):
        return self.net(x)

---

数据增强

Data argumentation 会减少出现过拟合的情况

1. Flip：翻转

2. Rotate  旋转

3. Random Move & Crop         随机裁剪

4. GAN : 生成更多的样本

5. Noise: N(0, 0.001)加高斯白噪声

这些操作都在torchvision包里面

 

通过这些操作可以根据少部分数据增加数据，增加数据后，情况会比原来好，但不会太好

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([    # Compose的操作类似于nn.Sequential里面
                       transforms.RandomHorizontalFlip(),    # 水平角度的翻转    （随机翻转-可能翻转也有可能不翻转）
                       transforms.RandomVerticalFlip(),    # 垂直方向
                       transforms.RandomRotation(15),    # 旋转方向，-15到15
                       transforms.RandomRotation([90, 180, 270]),    # 随机的从90度180度270度中挑一个角度旋转
                       transforms.Resize([32, 32]),    # 传入的参数为list，可以实现放缩
                       transforms.RandomCrop([28, 28]),    # 随机裁剪
                       transforms.ToTensor(),
                       # transforms.Normalize((0.1307,), (0.3081,))
                   ])),    
    batch_size=batch_size, shuffle=True)