使用LSTM进行简单时间序列预测（入门全流程，包括如何整理输入数据）

写在前面

前些天想使用LSTM进行实践序列的预测，但是网上查找的很多资料都没有很详细的讲明白输入数据长什么样子，如何处理输入数据等，并且他们的效果是假的。例如希望实现通过前30天的数据预测后10天的数据，但是他们实现的是每次都预测之后一天，导致预测效果非常好。
最终找到一篇入门文章，写的很好，我的代码基本都是借鉴的里面的，但是对里面一些模糊的东西我也做了解释。
我并没有分析LSTM的效果等，因为我不太了解。我只是介绍对一个简单的时间序列，如何整理输入、定义模型、训练和预测，从而跑通。

问题

假如我有一个时间序列，例如是前100天的价格数据，然后我希望借此预测后20天的数据，这里为了方便每一天的数据只有一个价格。但是每一天的数据也可以是多维的，也就是每一天都有好多特征。

具体思想

首先训练模型预测下一天数据的能力，训练完后，我们使用历史数据预测第114天的数据，预测后，我们暂时将第114天的数据看做真是数据，放入历史数据中，再用它预测第115天的数据，依次类推，最终预测完后30天的数据。

定义模型

我们会使用torch.nn.LSTM()加载LSTM层。其参数定义如下：

• input_size是我们输入的数据的维度，可以理解为我们每一天数据的维度。在这个问题里，每一天我们有的数据只有价格，因此input_size是1。如果每一天数据有n个特征，那么input_size是n。
• hidden_size是隐藏状态h的特征数。关于LSTM中的具体结构我还没有很清楚，可以查看一下知乎问题。在这里我认为可以随意设置。
• num_layers是我们要堆叠几个LSTM层。
  模型定义代码如下，和入门文章完全一样：

class RegLSTM(nn.Module):
    def __init__(self, inp_dim, out_dim, mid_dim, mid_layers):
        super(RegLSTM, self).__init__()

        self.rnn = nn.LSTM(inp_dim, mid_dim, mid_layers)  # rnn
        self.reg = nn.Sequential(
            nn.Linear(mid_dim, mid_dim),
            nn.Tanh(),
            nn.Linear(mid_dim, out_dim),
        )  # regression

    def forward(self, x):
        y = self.rnn(x)[0]  # y, (h, c) = self.rnn(x)     
        seq_len, batch_size, hid_dim = y.shape
        y = y.view(-1, hid_dim)                           
        y = self.reg(y)                                   
        y = y.view(seq_len, batch_size, -1)               
        return y

    """
    PyCharm Crtl+click nn.LSTM() jump to code of PyTorch:
    Examples::
        >>> rnn = nn.LSTM(10, 20, 2)
        >>> input = torch.randn(5, 3, 10)     # 5个时间步，也就是每个时间序列的长度是5,3表示一共有3个时间序列，10表示每个序列在每个时间步的维度是10
        >>> h0 = torch.randn(2, 3, 20)
        >>> c0 = torch.randn(2, 3, 20)
        >>> output, (hn, cn) = rnn(input, (h0, c0))
    """

    def output_y_hc(self, x, hc):

        y, hc = self.rnn(x, hc)  # y, (h, c) = self.rnn(x)

        seq_len, batch_size, hid_dim = y.size()
        y = y.view(-1, hid_dim)
        y = self.reg(y)
        y = y.view(seq_len, batch_size, -1)
        return y, hc

在LSTM内部，有h和c，可以理解为hidden和cell。模型中定义了两个函数forward()和output_y_hc，这里我还不太清楚，我认为可以理解为forward()函数在训练后预测时，会扔掉h和c，每次预测都用同一个h和c（可能是训练时最后一次的h和c，可能是随机的），output_y_hc()会一直返回h和c，从而下一次预测可以把h和c在带进去，一直用最新的h和c。具体问题我之后会再探究。
模型构造函数接受四个参数：inp_dim, out_dim, mid_dim, mid_layers，其中inp_dim, mid_dim, mid_layers是nn.LSTM()构造时传入的3个参数，输入维度是inp_dim，在这里是1，输出维度是mid_dim，这里可以自己定义。后面再跟两个全连接层，第一个全连接层是mid_dim to mid_dim，第二个全连接层是mid_dim to out_dim，也就是说，模型最后的输出维度是out_dim，在本问题中，我们希望预测的是每天的价格，所以out_dim也是1。

整理输入数据

• 经过尝试，LSTM对输入的时间序列长度似乎没有要求，也就是说我可以输入100天的历史数据进行训练，我也可以输入50天的历史数据进行训练。之后在训练完进行预测的时候，我也可以输入任意天数的历史数据预测未来的数据。
• 由于数据较少，我们只设置1个batch，也就是一次就把所有训练数据输入进去，然后迭代多个epoch进行训练。
• 我们使用113天的历史数据训练模型，预测后30天的数据。

方法1：只输入一条历史序列进行训练：

最简单的训练模式，我们把113天的历史数据一次性输入到模型中进行训练。113天的历史序列长这样：

[112., 118., 132., 129. …… 362., 348., 363.]

那这就是输入模型的x。那么输入模型的y是什么样呢？由于我们希望的是预测后一天的数据，所以我们每次都取后一天的数据，同样构成一个113天的序列，序列长这样：

[118., 132., 129., 121. …… 348., 363., 435.]

这就是输入模型的y。可以看到y就是x后移了1天。这里我认为，如果我们想预测后两天你的数据，那么我们的y就可以是x后移2天。

预处理数据

我们的数据是好几百，我们可以先预处理一下。对x和y，我们进行归一化，之后在模型训练好进行预测的时候，我们还要反归一化将数据还原。对于x和y我们分别归一化。之后在预测的时候，对于输入的x，我们要用训练集x的最大和最小值进行归一化处理，对于预测得到的y，我们要用训练集y的最大和最小值进行反归一化。所以我们要保存着训练集中x和y的最大值与最小值。
归一化和反归一化函数如下：

def minmaxscaler(x):
    minx = np.amin(x)
    maxx = np.amax(x)
    return (x - minx)/(maxx - minx), (minx, maxx)

def preminmaxscaler(x, minx, maxx):
    return (x - minx)/(maxx - minx)

def unminmaxscaler(x, minx, maxx):
    return x * (maxx - minx) + minx

preminmaxscaler是在预测的时候，我们用训练集的最大最小值去做归一化。
unminmaxscaler就是反归一化。

整理数据格式

我们构造好了输入数据的x和y，现在要把它们整理成模型希望的数据格式。LSTM希望的输入数据是3维，[x, y, z]：

• x是时间步，也就是每个序列的长度。
• y是序列个数，也就是我们希望同时处理多少个序列。
• z是输入数据维度，也就是对于每个时间序列，每一天的数据维数。

对于本问题，我们输入的是一个113天的历史序列，因此y是1。每一天都只有一个价格数据，因此z也是1。而x就是113。
对于y，y也是一个113天的序列，维度是1，数据格式也是[113, 1, 1]。

数据处理代码

bchain = np.array(
        [112., 118., 132., 129., 121., 135., 148., 148., 136., 119., 104.,
         118., 115., 126., 141., 135., 125., 149., 170., 170., 158., 133.,
         114., 140., 145., 150., 178., 163., 172., 178., 199., 199., 184.,
         162., 146., 166., 171., 180., 193., 181., 183., 218., 230., 242.,
         209., 191., 172., 194., 196., 196., 236., 235., 229., 243., 264.,
         272., 237., 211., 180., 201., 204., 188., 235., 227., 234., 264.,
         302., 293., 259., 229., 203., 229., 242., 233., 267., 269., 270.,
         315., 364., 347., 312., 274., 237., 278., 284., 277., 317., 313.,
         318., 374., 413., 405., 355., 306., 271., 306., 315., 301., 356.,
         348., 355., 422., 465., 467., 404., 347., 305., 336., 340., 318.,
         362., 348., 363., 435., 491., 505., 404., 359., 310., 337., 360.,
         342., 406., 396., 420., 472., 548., 559., 463., 407., 362., 405.,
         417., 391., 419., 461., 472., 535., 622., 606., 508., 461., 390.,
         432.], dtype=np.float32)
bchain = bchain[:, np.newaxis]

inp_dim = 1
out_dim = 1
mid_dim = 8
mid_layers = 1
data_x = bchain[:-1, :]
data_y = bchain[+1:, :]
# data_x shape：(143, 1)
# data_y shape：(143, 1)

train_size = 113
train_x = data_x[:train_size, :]
train_y = data_y[:train_size, :]
# train_x shape: (113, 1)
# train_y shape: (113, 1)

# 预处理数据  归一化
train_x, train_x_minmax = minmaxscaler(train_x)
train_y, train_y_minmax = minmaxscaler(train_y)

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 第一种操作，直接把batch_x batch_y这一个序列扔进去
batch_x = train_x[:, np.newaxis, :]
batch_y = train_y[:, np.newaxis, :]
batch_x = torch.tensor(batch_x, dtype=torch.float32, device=device)
batch_y = torch.tensor(batch_y, dtype=torch.float32, device=device)

方法2：输入多条短的历史序列进行训练：

我们也可以将使用类似于滑动窗口的方法，从原始数据里选取多段相同长度的序列，作为一条条的历史序列x，当然也要搭配y序列（就是把x序列右移一步）。
我们选定历史序列长度为40，一共选了25个序列，代码如下：

# 第二种操作，用滑动窗口的方法构造数据集
train_x_tensor = torch.tensor(train_x, dtype=torch.float32, device=device)
train_y_tensor = torch.tensor(train_y, dtype=torch.float32, device=device)
# 开始构造滑动窗口  40个为1个窗口，step为3
batch_x = list()
batch_y = list()

window_len = 40
for end in range(len(train_x_tensor), window_len, -3):
    batch_x.append(train_x_tensor[end-40:end])
    batch_y.append(train_y_tensor[end-40:end])

# batch_x的shape是(25, 40, 1)  25个时间序列，每个时间序列是40个时间步

from torch.nn.utils.rnn import pad_sequence
batch_x = pad_sequence(batch_x)
batch_y = pad_sequence(batch_y)

# batch_x的shape是(40, 25, 1)   输入模型的时候可以25个时间序列并行处理

我们通过pad_sequence将数据整理成LSTM希望的格式。
比如我们本来有3条历史序列，分别是[1, 2, 3]，[4, 5, 6]，[7, 8, 9]，但是我们将它们整理成的格式为：

原本是：               整理成：
[[1, 2, 3],                [[[1], [4], [7]],
 [4, 5, 6],                 [[2], [5], [8]],
 [7, 8, 9]]                 [[3], [6], [9]]]

这样，每一列是一个序列，一共有3个历史序列。每一行是一个时间步，这样整理数据，模型就能一行一行的处理，从而同时处理3个序列。
对于训练用的x和y，我们都整理成一样的格式。只不过在一般的情境中，x的维度要高一点，比如每一天（也就是一个时间步），一共有n个数据表示，也就是说x的维度是n，也就是说在定义LSTM的时候，input_size是n。假如我们有m个序列，每个序列有z个时间步，最后的x要整理成**[z, m, n]**。

模型训练和预测

模型训练

有了训练用的x和y，我们就可以将其输入到模型进行训练。代码如下：

# 加载模型
model = RegLSTM(inp_dim, out_dim, mid_dim, mid_layers).to(device)
loss = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-2)

# 开始训练
print("Training......")
for e in range(801):
    out = model(batch_x)

    Loss = loss(out, batch_y)

    optimizer.zero_grad()
    Loss.backward()
    optimizer.step()

    if e % 10 == 0:
        print('Epoch: {:4}, Loss: {:.5f}'.format(e, Loss.item()))
torch.save(model.state_dict(), './net.pth')
print("Save in:", './net.pth')

模型预测

预测的时候，我们还是要输入一个序列x，得到一个输出序列y。由于在训练时输出序列是输入序列右移一步，因此对于得到的y，其最后一个值就是我们预测的下一天的数据。
对于输入的序列x，序列长度任意，我在尝试的时候发现序列长度长一点和短一点（甚至序列长度是1），预测的效果好像没有差别，这可能证明LSTM的预测效果并不好。我也不太清楚。

new_data_x = data_x.copy()
new_data_x[train_size:] = 0

test_len = 40

eval_size = 1
zero_ten = torch.zeros((mid_layers, eval_size, mid_dim), dtype=torch.float32, device=device)

for i in range(train_size, len(new_data_x)):  # 要预测的是i
    test_x = new_data_x[i-test_len:i, np.newaxis, :]
    test_x = preminmaxscaler(test_x, train_x_minmax[0], train_x_minmax[1])
    batch_test_x = torch.tensor(test_x, dtype=torch.float32, device=device)

    if i == train_size:
        test_y, hc = model.output_y_hc(batch_test_x, (zero_ten, zero_ten))
    else:
        test_y, hc = model.output_y_hc(batch_test_x[-2:], hc)
    test_y = model(batch_test_x)
    predict_y = test_y[-1].item()
    predict_y = unminmaxscaler(predict_y, train_x_minmax[0], train_y_minmax[1])
    new_data_x[i] = predict_y

• new_data_x中，前103天是历史数据，后面的天数是我们要预测的，因此其值都设置为0。
• 我们每次输入40天的数据，并希望预测得到下一天，这样依次将104天、105天直到最后一天的数据预测出来。
• test_x是我们每次输入的40天的历史序列，将其整理成**[40, 1, 1]**的格式，并进行归一化，然后输入模型。
• 得到的test_y也是一个40天的序列，最后一个值就是我们预测的下一天的值。使用反归一化将其还原，就是预测的下一天的值。我们将其天道new_data_x的相应位置中。
• hc就是模型的隐状态，这样不断返回模型隐状态，再输入到模型中，应该是效果会比较好。这个我不太清楚。

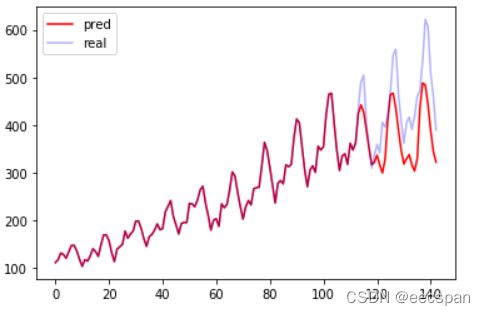
预测效果

可以把效果作图：

plt.plot(new_data_x, 'r', label='pred')
plt.plot(data_x, 'b', label='real', alpha=0.3)
plt.legend(loc='best')

我使用第一种训练数据整理方法，效果如下：