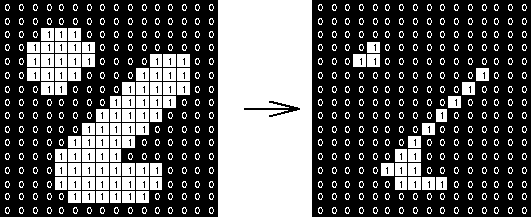图像处理-006形态变换
图像处理-006形态变换
图像的形态变换(Morphological Transformations)是基于图像外形的操作，通常用于处理二值图像。基本的形态变换有腐蚀(Erosion)，膨胀(Dilation)，开操作(Opening)，闭操作(Closing)。
腐蚀和膨胀是图像形态学中两种最基本的运算类型，运算时两者均需输入待腐蚀/膨胀的图形和用于运算的结构化元素集(卷积核)，图像是用二维数组表示的，卷积核也是用二维数组表示的，因此输入数据被视为坐标的集合，仅在二值图像和灰度图像时存在区别，卷积核决定了图像被腐蚀或膨胀的范围。
二值图像中白色表示前景色，黑色表示背景色，某些场景下是相反的。图像坐标集视为图像前景色的二维欧几里得坐标。在该坐标系中常取图像的某个角为坐标原点，所以所有坐标点都是正数。
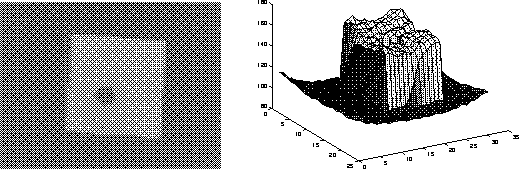
灰度图像中，像素亮度表示为基础平面的高度，灰度图像视为三维欧拉空间的表面。如图006-1所示，
结构化元素集(类似于图像模糊中的卷积核)是一组点坐标的集合，与输入图像坐标集相比比结构元素较小，坐标原点(锚点)在中心，所以其在负值。结构元素决定的了腐蚀/膨胀对输入图像的影响程度。
OpenCV中提供了getStructuringElement()， 通过该函数得到用于形态操作的kernel.
Mat cv::getStructuringElement(int shape, #形态变换类型，
Size ksize, #kernel大小
Point anchor = Point(-1,-1) #锚点位置，默认中心位置
)
Python:
cv.getStructuringElement(shape, ksize[, anchor] ) -> retval
其中，shape由三种类型：参阅MorphShapes
-
MORPH_RECT: kernel中所有元素均为1, 即 E i j = 1 E_{ij}=1 Eij=1 , 7*7 的kernel形如：
[ 1, 1, 1, 1, 1, 1, 1;
1, 1, 1, 1, 1, 1, 1;
1, 1, 1, 1, 1, 1, 1;
1, 1, 1, 1, 1, 1, 1;
1, 1, 1, 1, 1, 1, 1;
1, 1, 1, 1, 1, 1, 1;
1, 1, 1, 1, 1, 1, 1] -
MORPH_CROSS: kernel中为1的元素呈十字型分布，即以锚点为中心的十字型
E i j = { 1 if i = anchor.y o r j = anchor.x 0 otherwise E_{ij} = \begin{cases} 1 & \texttt{if } {i=\texttt{anchor.y } {or } {j=\texttt{anchor.x}}} \\0 & \texttt{otherwise} \end{cases} Eij={10if i=anchor.y orj=anchor.xotherwise
7*7的kernel形如:
[ 0, 0, 0, 1, 0, 0, 0;
0, 0, 0, 1, 0, 0, 0;
0, 0, 0, 1, 0, 0, 0;
1, 1, 1, 1, 1, 1, 1;
0, 0, 0, 1, 0, 0, 0;
0, 0, 0, 1, 0, 0, 0;
0, 0, 0, 1, 0, 0, 0] -
MORPH_ELLIPSE: kernel中为1的元素以kernel内接椭圆的形式分布，形如：
[ 0, 0, 0, 1, 0, 0, 0;
0, 1, 1, 1, 1, 1, 0;
1, 1, 1, 1, 1, 1, 1;
1, 1, 1, 1, 1, 1, 1;
1, 1, 1, 1, 1, 1, 1;
0, 1, 1, 1, 1, 1, 0;
0, 0, 0, 1, 0, 0, 0]
腐蚀(Erosion)
腐蚀是图像形态学中一种基本运算，用于寻找图像中的极小区域，类似于“领域被蚕食”，将图像中的高亮区域或白色部分进行缩减细化，其运行结果图比原图的高亮区域更小。
定义：
-
假设X是二值图像的欧拉坐标集，K为卷积核的坐标集；
-
令Kx表示K的平移，使其锚点位于x;
-
那么K对X的腐蚀表示为：对所有的的X的集合，使得Kx是X的子集。
假设二值图像白色区域像素为1， 黑色区域像素为0，图像做腐蚀时，将kernel置于图像之上，锚点依次与图像中的坐标P对应，P与kernel中各元素做加法运算，取运算后的最小值做为P处的值，其公式如006-1所示：
dst ( x , y ) = min ( x ′ , y ′ ) : element ( x ′ , y ′ ) ≠ 0 src ( x + x ′ , y + y ′ ) (006-1) \texttt{dst} (x,y) = \min _{(x',y'): \, \texttt{element} (x',y') \ne0 } \texttt{src} (x+x',y+y') \tag{006-1} dst(x,y)=(x′,y′):element(x′,y′)=0minsrc(x+x′,y+y′)(006-1)
二值图像中只含有0，1两元素，kernel只有1一种元素，因此，若kernel下覆盖下的图像像素值均为1，则图像像素保持不变，否则kernel覆盖下的图像区域的像素置为0。
kernle为3*3的二值图像的腐蚀效果如图006-2所示:
腐蚀时，根据kernel的大小图像边缘的部分白色像素被丢弃，对消除图像中的白色噪声，分离相连的对象非常有用。kernel越大腐蚀效果越明显。
OpenCV中，使用erode做腐蚀变换，其详细描述如下:
void cv::erode(InputArray src, #输入图像
OutputArray dst, #与输入图像同类型，同大小的输出图像
InputArray kernel, #用于腐蚀的结构化元素
Point anchor = Point(-1,-1), #kernel中锚点元素的位置，默认(-1,-1)为kernel的中心点
int iterations = 1, #腐蚀操作迭代次数
int borderType = BORDER_CONSTANT, #腐蚀时边界像素展拓方式
const Scalar & borderValue = morphologyDefaultBorderValue() #边界值
)
Python:
cv.erode(src, kernel[, dst[, anchor[, iterations[, borderType[, borderValue]]]]]) -> dst
实现代码: C++
/**
* 腐蚀
* @param img
* @return
*/
int Morphological::erode_transform(const Mat &img) {
logger_info("======erode_transform=====================");
// kernel size为7*7
Mat kernel = getStructuringElement(MORPH_RECT, Size(7, 7));
Mat dst;
erode(img, dst, kernel);
imshow("erode", dst);
return EXIT_SUCCESS;
}
实现代码:python
# 腐蚀
def erode_transform(origin_img):
titles = ["origin_image"]
images = [cv.cvtColor(origin_img, cv.COLOR_BGR2RGB)]
for i in range(3, 13, 2):
kernel = cv.getStructuringElement(cv.MORPH_RECT, (i, i))
dst = cv.erode(origin_img, kernel)
titles.append("erode_kernel_" + str(i))
images.append(cv.cvtColor(dst, cv.COLOR_BGR2RGB))
for i in range(6):
plt.subplot(2, 3, i + 1)
plt.imshow(images[i], 'gray', vmin=0, vmax=255)
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
腐蚀效果如图006-3所示:
膨胀(Dilation)
膨胀是图像形态学中另一种基本运算，用于寻找图像中的极大区域，类似于“领域扩张”，将图像中的高亮区域或白色部分进行扩张，其运行结果图比原图的高亮区域更大。
膨胀与腐蚀类似，不同的是膨胀是腐蚀的相反操作。
定义：
-
假设X是二值图像的欧拉坐标集，K为卷积核的坐标集；
-
令Kx表示K的平移，使其锚点位于x;
-
那么K对X的膨胀表示为：对所有的的X的集合，使得Kx与X的交集是非空的。
假设二值图像白色区域像素为1， 黑色区域像素为0，图像做腐蚀时，将kernel置于图像之上，锚点依次与图像中的坐标P对应，P与kernel中各元素做加法运算，取运算后的最大值做为P处的值，其公式如006-2所示：
dst ( x , y ) = max ( x ′ , y ′ ) : element ( x ′ , y ′ ) ≠ 0 src ( x + x ′ , y + y ′ ) (006-2) \texttt{dst} (x,y) = \max _{(x',y'): \, \texttt{element} (x',y') \ne0 } \texttt{src} (x+x',y+y') \tag{006-2} dst(x,y)=(x′,y′):element(x′,y′)=0maxsrc(x+x′,y+y′)(006-2)
假设二值图像白色区域像素为1， 黑色区域像素为0，图像做膨胀时，将卷积核置于图像之上，锚点依次与图像中的坐标对应，若卷积核下覆盖下的图像像素值均为0，则图像像素保持不变，否则kernel覆盖下的图像区域的像素置为1.
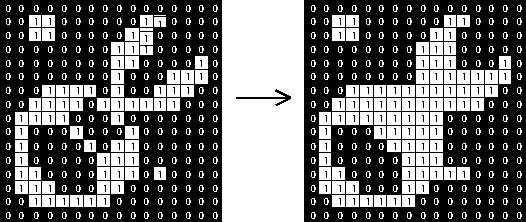
kernle为3*3的二值图像的膨胀效果如图006-5所示:
opencv提供dilate()函数来进行膨胀，其函数声明如下:
void cv::dilate(InputArray src, #输入图像
OutputArray dst, #与输入图像同类型，同大小的输出图像
InputArray kernel, #用于膨胀的结构化元素
Point anchor = Point(-1,-1), #kernel中锚点元素的位置，默认(-1,-1)为kernel的中心点
int iterations = 1, #膨胀操作迭代次数
int borderType = BORDER_CONSTANT, #膨胀时边界像素展拓方式
const Scalar & borderValue = morphologyDefaultBorderValue()) #边界值
Python:
cv.dilate(src, kernel[, dst[, anchor[, iterations[, borderType[, borderValue]]]]]) -> dst
实现代码: C++
/**
* 膨胀
* @param img
* @return
*/
int Morphological::dilation_transform(const Mat &img) {
logger_info("======dilation_transform=====================");
// kernel size为7*7
Mat kernel = getStructuringElement(MORPH_RECT, Size(7, 7));
Mat dst;
dilate(img, dst, kernel);
imshow("dilate", dst);
return EXIT_SUCCESS;
}
实现代码: python
/**
* 膨胀
* @param img
* @return
*/
int Morphological::dilation_transform(const Mat &img) {
logger_info("======dilation_transform=====================");
// kernel size为7*7
Mat kernel = getStructuringElement(MORPH_RECT, Size(7, 7));
Mat dst;
dilate(img, dst, kernel);
imshow("dilate", dst);
return EXIT_SUCCESS;
}
不同kernel大小的膨胀效果如图006-6所示:
Opening(开操作)
虽然腐蚀可以方便的消除图像中的白噪声(椒盐噪声中的白噪声)，缺点是影响图像中所有的白色区域，未对白色区域的边缘做区分。
图像的开操作和闭操作源于腐蚀与膨胀。开操作是使用相同的kernel先对图像进行腐蚀，然后再进行膨胀。开操作会保留与源图像类似的轮廓。
dst = o p e n ( src , element ) = d i l a t e ( e r o d e ( src , element ) ) \texttt{dst} = \mathrm{open} ( \texttt{src} , \texttt{element} )= \mathrm{dilate} ( \mathrm{erode} ( \texttt{src} , \texttt{element} )) dst=open(src,element)=dilate(erode(src,element))
腐蚀消除图像的白噪声的同时使得图像中物体瘦身，然后再膨胀，瘦身的物体再次变大，但消失的白噪声不会再出现。开操作消除图像较小连通域，保留较大连通域，往往用来分离比邻近点亮一些的斑块，对处理图像中连接物体断裂部分非常有效。
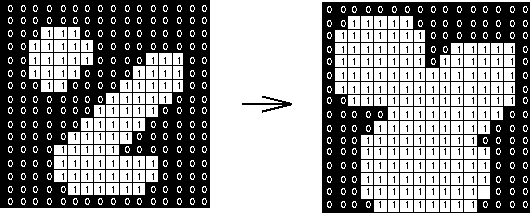
kernle为3*3的二值图像的开操作效果如图006-7所示:
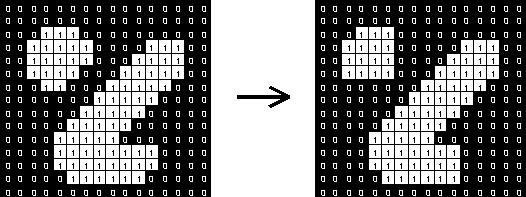
OpenCV提供函数morphologyEx()融合腐蚀、膨胀操作来实现高级形态变换，如开运算，闭运算。基函数声明如下:
void cv::morphologyEx(InputArray src, #输入图像
OutputArray dst, #与输入图像同类型、同大小的输出图像
int op, # 操作类型
InputArray kernel, #用于形态变换的kernel
Point anchor = Point(-1,-1), #
int iterations = 1, #迭代次数
int borderType = BORDER_CONSTANT, #边界像素展拓方式
const Scalar & borderValue = morphologyDefaultBorderValue())
Python:
cv.morphologyEx(src, op, kernel[, dst[, anchor[, iterations[, borderType[, borderValue]]]]] ) -> dst
其中的op参数参阅MorphTypes
实现代码: C++
/**
* 开运算
* @param img
* @return
*/
int Morphological::opening_transform(const Mat &img) {
logger_info("======opening_transform=====================");
// kernel size为7*7
Mat kernel = getStructuringElement(MORPH_OPEN, Size(7, 7));
Mat dst;
morphologyEx(img, dst, MORPH_OPEN, kernel);
imshow("opening", dst);
return EXIT_SUCCESS;
}
实现代码:Python
# 开运算
def opening_transform(origin_img):
titles = ["origin_image"]
images = [cv.cvtColor(origin_img, cv.COLOR_BGR2RGB)]
for i in range(3, 13, 2):
kernel = cv.getStructuringElement(cv.MORPH_RECT, (i, i))
dst = cv.morphologyEx(origin_img, cv.MORPH_OPEN, kernel)
titles.append("opening_kernel_" + str(i))
images.append(cv.cvtColor(dst, cv.COLOR_BGR2RGB))
for i in range(6):
plt.subplot(2, 3, i + 1)
plt.imshow(images[i], 'gray', vmin=0, vmax=255)
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
开操作效果如图006-8所示:
Closing(闭操作)
虽然膨胀可以方便的消除图像中的黑噪声(椒盐噪声中的黑噪声)，缺点是未充分考虑图像中黑色的区域，会将非黑噪声区域当做噪声处理。处理后图像的轮廓与源图像中的物体有较大差异，甚至与源图像轮廓完全不同。
闭操作与开操作相反。闭操作是先膨胀后腐蚀，闭操作去除连通域内的小型空洞，平滑物体轮廓，连接两个临近的连通域，保持源图像的基本轮廓无较大变化，用来分离比邻近点一些的斑块。因此，闭操作对消除图像中物体的黑点(椒盐噪声中的黑点)非常有效。
dst = c l o s e ( src , element ) = e r o d e ( d i l a t e ( src , element ) ) \texttt{dst} = \mathrm{close} ( \texttt{src} , \texttt{element} )= \mathrm{erode} ( \mathrm{dilate} ( \texttt{src} , \texttt{element} )) dst=close(src,element)=erode(dilate(src,element))
kernle为3*3的二值图像的闭操作效果如图006-5所示:
实现代码:C++
/**
* 闭运算
* @param img
* @return
*/
int Morphological::closing_transform(const Mat &img) {
logger_info("======closing_transform=====================");
// kernel size为7*7
Mat kernel = getStructuringElement(MORPH_RECT, Size(7, 7));
cout << "kernel " << kernel << endl;
Mat dst;
morphologyEx(img, dst, MORPH_CLOSE, kernel);
imshow("closing", dst);
return EXIT_SUCCESS;
}
实现代码：python
# 闭运算
def closing_transform(origin_img):
titles = ["origin_image"]
images = [cv.cvtColor(origin_img, cv.COLOR_BGR2RGB)]
for i in range(3, 13, 2):
kernel = cv.getStructuringElement(cv.MORPH_RECT, (i, i))
dst = cv.morphologyEx(origin_img, cv.MORPH_CLOSE, kernel)
titles.append("closing_kernel_" + str(i))
images.append(cv.cvtColor(dst, cv.COLOR_BGR2RGB))
for i in range(6):
plt.subplot(2, 3, i + 1)
plt.imshow(images[i], 'gray', vmin=0, vmax=255)
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
不同kernel大小闭操作效果如图006-10所示:
Morphological Gradient(形态学梯度)
梯度运算指二值图像膨胀运算与腐蚀运算的差。该操作可以完美提取图像中物体的轮廓。膨胀与腐蚀时使用相同的kernel。即:
dst = m o r p h _ g r a d ( src , element ) = d i l a t e ( src , element ) − e r o d e ( src , element ) \texttt{dst} = \mathrm{morph\_grad} ( \texttt{src} , \texttt{element} )= \mathrm{dilate} ( \texttt{src} , \texttt{element} )- \mathrm{erode} ( \texttt{src} , \texttt{element} ) dst=morph_grad(src,element)=dilate(src,element)−erode(src,element)
代码实现: c++
/**
* 梯度
* @param img
* @return
*/
int Morphological::gradient_transform(const Mat &img) {
logger_info("======gradient_transform=====================");
// kernel size为7*7
Mat kernel = getStructuringElement(MORPH_RECT, Size(7, 7));
Mat dst;
morphologyEx(img, dst, MORPH_GRADIENT, kernel);
imshow("gradient", dst);
return EXIT_SUCCESS;
}
实现代码: python
# 梯度
def gradient_transform(origin_img):
titles = ["origin_image"]
images = [cv.cvtColor(origin_img, cv.COLOR_BGR2RGB)]
for i in range(3, 13, 2):
kernel = cv.getStructuringElement(cv.MORPH_RECT, (i, i))
dst = cv.morphologyEx(origin_img, cv.MORPH_GRADIENT, kernel)
titles.append("gradient_kernel_" + str(i))
images.append(cv.cvtColor(dst, cv.COLOR_BGR2RGB))
for i in range(6):
plt.subplot(2, 3, i + 1)
plt.imshow(images[i], 'gray', vmin=0, vmax=255)
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
不同kernel大小梯度操作效果如图006-11所示: 从效果图中可以看出，kernel越小梯度效果越明显。
图006-11 kernel不同size的二值图像的梯度操作效果
Top Hat(顶帽)
顶帽操作指二值图像与开运算后的差。即:
dst = t o p h a t ( src , element ) = src − o p e n ( src , element ) \texttt{dst} = \mathrm{tophat} ( \texttt{src} , \texttt{element} )= \texttt{src} - \mathrm{open} ( \texttt{src} , \texttt{element} ) dst=tophat(src,element)=src−open(src,element)
代码实现: c++
/**
* 顶帽
* @param img
* @return
*/
int Morphological::top_hat_transform(const Mat &img) {
logger_info("======top_hat_transform=====================");
// kernel size为7*7
Mat kernel = getStructuringElement(MORPH_RECT, Size(3, 3));
Mat dst;
morphologyEx(img, dst, MORPH_TOPHAT, kernel);
imshow("top_hat", dst);
return EXIT_SUCCESS;
}
代码实现: python
# 顶帽
def top_hat_transform(origin_img):
titles = ["origin_image"]
images = [cv.cvtColor(origin_img, cv.COLOR_BGR2RGB)]
for i in range(3, 13, 2):
kernel = cv.getStructuringElement(cv.MORPH_RECT, (i, i))
dst = cv.morphologyEx(origin_img, cv.MORPH_TOPHAT, kernel)
titles.append("top_hat_kernel_" + str(i))
images.append(cv.cvtColor(dst, cv.COLOR_BGR2RGB))
for i in range(6):
plt.subplot(2, 3, i + 1)
plt.imshow(images[i], 'gray', vmin=0, vmax=255)
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
不同kernel大小下的顶帽操作效果如图006-12所示
图006-12 kernel不同size的二值图像的顶帽操作效果
因开运算放大了裂缝或者局部低亮度的区域，从原图中减去开运算后的图，得到的效果图突出了比原图轮廓周围的区域更明亮的区域，且这一操作与选择的核的大小有关。
顶帽运算往往是用来分离比邻近点亮一些的斑块。在一副图像具有大幅的背景而微小物品比较有规律的情况下，可以使用顶帽运算进行背景提取。
Black Hat(黑帽)
黑帽操作指闭运算与二值图像的差。即:
dst = b l a c k h a t ( src , element ) = c l o s e ( src , element ) − src \texttt{dst} = \mathrm{blackhat} ( \texttt{src} , \texttt{element} )= \mathrm{close} ( \texttt{src} , \texttt{element} )- \texttt{src} dst=blackhat(src,element)=close(src,element)−src
代码实现: c++
/**
* 黑帽
* @param img
* @return
*/
int Morphological::black_top_transform(const Mat &img) {
logger_info("======top_hat_transform=====================");
// kernel size为7*7
Mat kernel = getStructuringElement(MORPH_RECT, Size(3, 3));
Mat dst;
morphologyEx(img, dst, MORPH_BLACKHAT, kernel);
imshow("black_hat", dst);
return EXIT_SUCCESS;
}
实现代码: python
# 黑帽
def black_hat_transform(origin_img):
titles = ["origin_image"]
images = [cv.cvtColor(origin_img, cv.COLOR_BGR2RGB)]
for i in range(3, 13, 2):
kernel = cv.getStructuringElement(cv.MORPH_RECT, (i, i))
dst = cv.morphologyEx(origin_img, cv.MORPH_BLACKHAT, kernel)
titles.append("black_hat_kernel_" + str(i))
images.append(cv.cvtColor(dst, cv.COLOR_BGR2RGB))
for i in range(6):
plt.subplot(2, 3, i + 1)
plt.imshow(images[i], 'gray', vmin=0, vmax=255)
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
不同kernel大小下的顶帽操作效果如图006-13所示
黑帽运算后的效果图突出了比原图轮廓周围的区域更暗的区域，且这一操作和选择的核的大小相关，黑帽运算用来分离比邻近点暗一些的斑块，效果图有着非常完美的轮廓。
参考文献：
-
https://docs.opencv.org/4.6.0/d9/d61/tutorial_py_morphological_ops.html
-
https://homepages.inf.ed.ac.uk/rbf/HIPR2/morops.htm
-
http://www.cs.cmu.edu/~cil/vision.html
-
https://docs.opencv.org/4.6.0/db/d06/tutorial_hitOrMiss.html