SVM(原理公式推导)

参考博客1
参考博客2

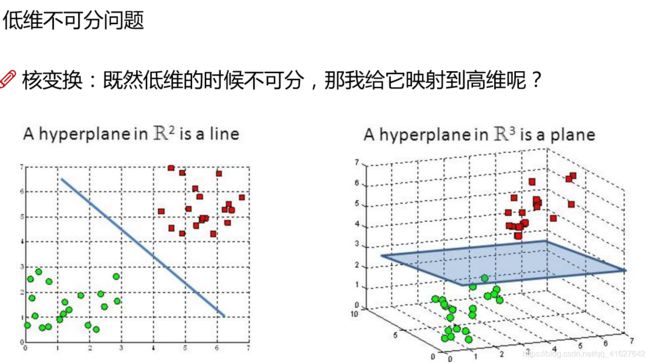
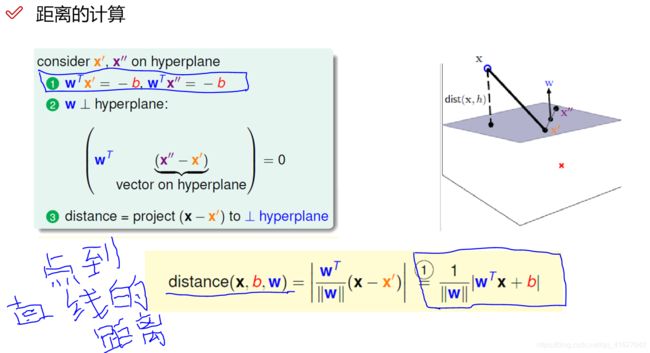
点到平面内一条直线的距离

如下图x’,x’'是一个平面内的两点，W是平面内的法向量，则点到直线的距离公式为：

对于如下的一些训练样本：



min求离直线最近的点，max使距离最远。1/w^{2的最大，转化为w}2/2。


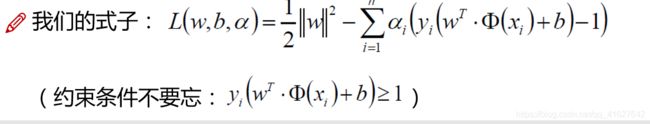
s


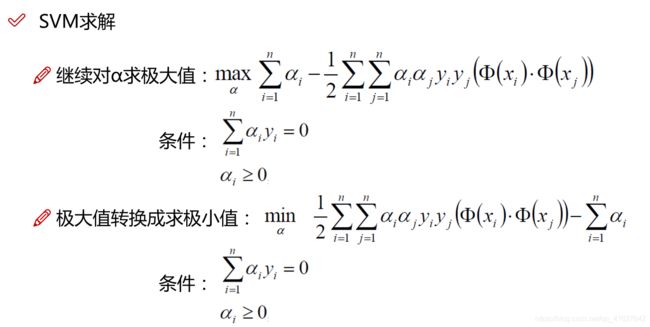
通过上面的公式推导，我们转化为以下三个步骤：



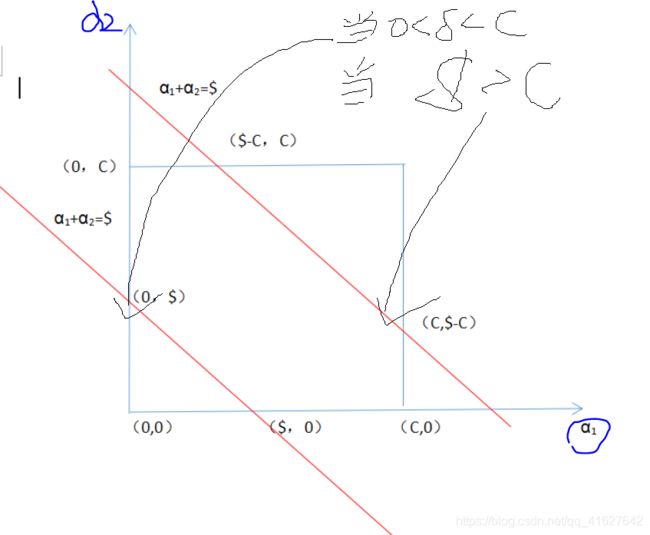
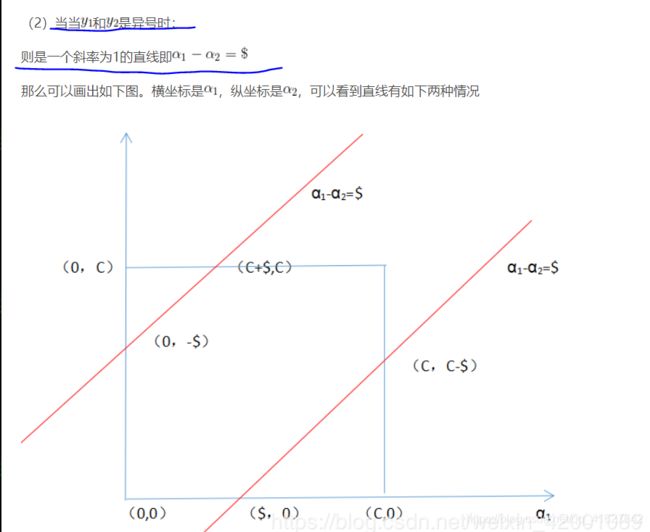
由于引入的松弛因子Bi,C是对松弛因子的严格程度。C越大，代表超平面越严格,意味着分类严格不能有错误；C很小，意味着可以有大的错误容忍。






通过求导和约束条件，我们知道ai系数再不通的取值范围内的分布。

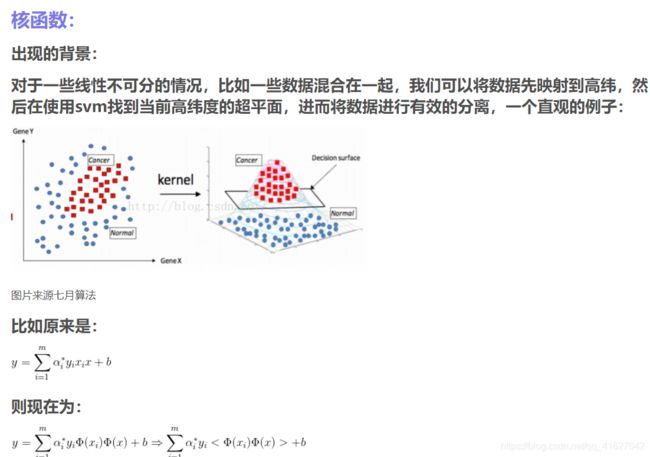
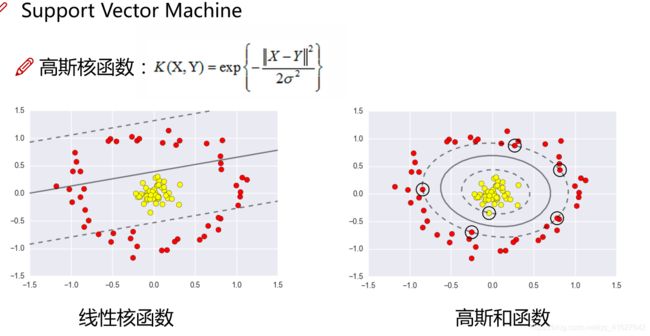
核函数介绍

有四种核函数，线性核函数、多项式核函数、高斯核函数，sigmoid核函数。

首先第一步，求解系数ai

为什么是二元一次方程呢？很简单由原始优化目标可以看出基本单元就是\alpha _{i}\alpha _{j},然后就是组合相加，所以最高次数就是2次，前面还有单次项，后面有常数项，所以最后归结起来就是一个一元二次方程

开始求解目标函数

将我们的优化目标函数展开，得到：

xi和xj是点积。例如（3，3）T(3,3)=18




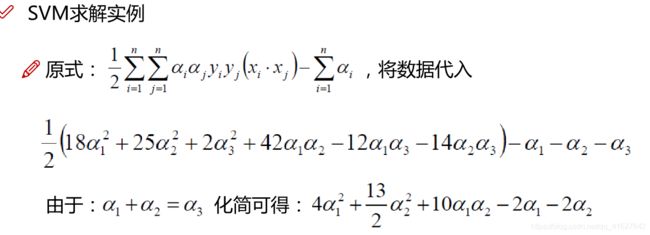
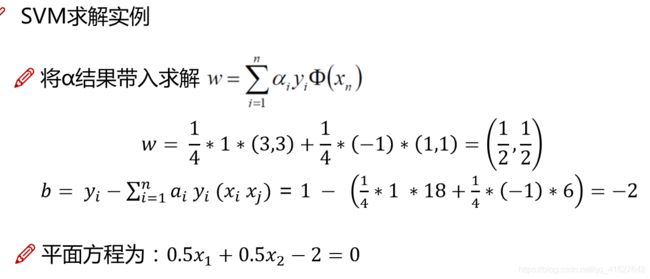
总结：对于a=0的是不起作用的对于决策边界的形成。






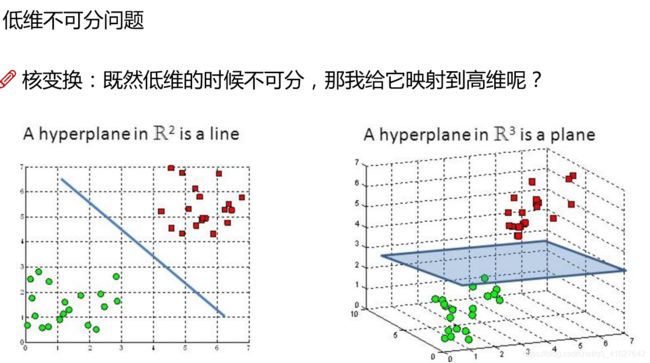
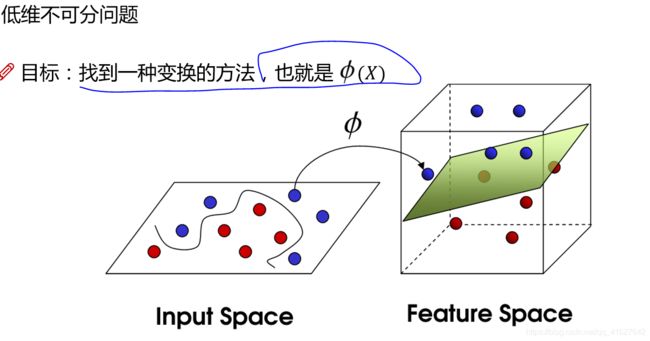
对于svm一边选择高斯核函数将低维映射到高维。

代码解析

计算a系数和b

#最简版本SMO算法
    #dataMatIn为X,classLabels为y,C是核函数对应的系数C
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = np.mat(dataMatIn); #将X转换为矩阵
    labelMat = np.mat(classLabels).transpose()#将y转换为矩阵并转置为一列
    b = 0; 
    m,n = np.shape(dataMatrix)#获取样本的行列
    alphas = np.mat(np.zeros((m,1)))#定义a系数的初始值，m行一列
    iter_num = 0#初始迭代次数
    while (iter_num < maxIter):
        alphaPairsChanged = 0#记录有多少被优化
        #遍历完这一遍所有的\alpha后，alphaPairsChange用以记录看有多少对被优化啦
        for i in range(m):
            #注意一
            #fxi由公式w=aiyixi的和组成，带入y=wx+b里形成了fxi,求每一个样本的预测值
            fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i])#误差ei=yi*-yi
             # 一旦alphas等于0或C，那么它们就巳经在“边界”上了，因而不再能够减小或增大，因此也就不值得再对它们进行优化了
             #由公式推导，当ai=0,点再两条间隔线外侧，当ai=C,再间隔线内侧，0
             #toler代表容忍错误值
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                #开始优化，选择ai对。随机选择第二个alpha值j（不等于i）
                j = selectJrand(i,m)
                #就按第二个alpha值j对应的预测值
                fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b#求yj*
                Ej = fXj - float(labelMat[j])
                alphaIold = alphas[i].copy();
                alphaJold = alphas[j].copy();
                # 下述判断保证alpha[j]在0，C之间
                #yi和yj不同号时，yi和yj同号时，当L=H时，代表ai和aj都在边界上，不需要优化
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                    
                if L==H: 
                    print("L==H"); 
                    continue
                #注意二
                #eta求的是K11+K22-2K12，现在是负得eta,所以保留小于0得值
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                if eta >= 0: 
                    print("eta>=0"); 
                    continue
                #计算获取新的alpha[j]
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta #求解出来
                # 调整alpha aj的值，使值在(H,L)区间
                alphas[j] = clipAlpha(alphas[j],H,L)
               #推导部分的\alpha _{2}更新，只不过这里有一步如果变化太小我们就不更新了，直接跳过
                if (abs(alphas[j] - alphaJold) < 0.00001): print("alpha_j变化小，不需要更新"); continue
                #注意三，\alpha _{1}的更新即大小
                #ai+=ai+yiyj(ajold-ajnew)
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
 
                #注意四，推导的b的更新
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
             
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2)/2.0
               
                alphaPairsChanged += 1
              
                print("第%d次迭代 样本:%d, alpha优化次数:%d" % (iter_num,i,alphaPairsChanged))
       #alphaPairsChange为0时，说明我们这一遍走下来，说明\alpha都很好啦，没有优化的必要啦，我们将iter_num加一
        if (alphaPairsChanged == 0): 
            iter_num += 1
        else: iter_num = 0
        print("迭代次数: %d" % iter_num)
    #注意五
    return b,alphas
'''
smo函数的alphaPairsChanged和iter_num以及maxIter的参数意义，maxIter是最外部的大循环，是人为设定的最大循环次数，循环为最大次数后就强行结束返回，在每一个大循环下都有一个for循环，用以遍历一遍所有的，遍历完这一遍所有的后，alphaPairsChange用以记录看有多少对被优化啦，如果alphaPairsChange不为0，
即这一遍走下来后，我们进行了优化，也就代表目前还不够好，所以我们将iter_num设为0，继续优化，当alphaPairsChange为0时，说明我们这一遍走下来，说明都很好啦，没有优化的必要啦，我们将iter_num加一，
接着下一遍再去整体看看，如果还是alphaPairsChange为0，恩恩，不错，不错，将iter_num再加一，如果iter_num到了maxIter即连续进行了maxIter遍整体（for）观察都没发现需要优化的，说明足够好了，返回吧！
'''

辅助函数

# -*- coding: utf-8 -*-
import random
import  numpy  as np
import matplotlib.pyplot as plt
#辅助函数一，第一个函数的作用就是用来选择\alpha对
def selectJrand(i, m):
    j = i  
    while (j == i):
        j = int(random.uniform(0, m))
    return j
#辅助函函数二，函数就是为了将\alpha规划到[0,C]范围内
def clipAlpha(aj,H,L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

计算出来权重 w

def calcWs(dataMat, labelMat, alphas):
    alphas, dataMat, labelMat = np.array(alphas), np.array(dataMat), np.array(labelMat)#把输入转化为数组形式
    w = np.dot((np.tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)#根据训练出来的\alpha生成w，1.np.tile((1,2))沿X轴复制
    return w.tolist()

展示图像

def showClassifer(dataMat,labelMat,alphas, w, b):
    data_plus = []   #正样本数据                               
    data_minus = [] #负样本数据
    #注意六
    #我们把原始点画出来，不同的颜色代表不同的分离（橙色的点对应的标签是-1，蓝色的点对应的标签是1）
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus)    #列表转换为数组形式          
    data_minus_np = np.array(data_minus)
    #画散点图            
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)   
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7) 
    #注意七
    #画出训练出来的超平面
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    #y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
    y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
    plt.plot([x1, x2], [y1, y2])
    #注意八，画出来最近的样本点
    #即在点在两条间隔线外则，对应前面的系数\alpha为0，在两条间隔线里面的对应的系数为C，在两条间隔线上的点对应的系数在0和C之间。
    for i, alpha in enumerate(alphas):
        if 0.6>abs(alpha) > 0:
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
        if 0.6==abs(alpha) :
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='yellow')
    plt.show()
 
if __name__=="__main__":
    x=[[1,8],[3,20],[1,15],[3,35],[5,35],[4,40],[7,80],[6,49],[1.5,25],[3.5,45],[4.5,50],[6.5,15],[5.5,20],[5.8,74],[2.5,5]]
    y=[1,1,-1,-1,1,-1,-1,1,-1,-1,-1,1,1,-1,1]
    b,alphas = smoSimple(x,y,0.6,0.001,40)
    w = calcWs(x,y,alphas)
    showClassifer(x,y,alphas, w, b)  

改进得SMO算法

#Platt SMO：，改进其是SMO算法的一个改进版，速度更快
import numpy as np
import matplotlib.pyplot as plt


#首先optStruct函数定义了一个类作为数据结构来存储一些信息，这里面的alphas就是我们的\alpha，
#eCache第一列就是一个是否有效的标志位，第二列存储着误差值E
class optStructK:
    def __init__(self,dataMatIn, classLabels, C, toler, kTup):  # Initialize the structure with the parameters 
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = np.shape(dataMatIn)[0]
        self.alphas = np.mat(np.zeros((self.m,1)))
        self.b = 0
        self.eCache = np.mat(np.zeros((self.m,2))) #第一列是有效的标志位      
        #""" knrnel        
        self.K = np.mat(np.zeros((self.m,self.m)))#函数增加了一个字段即K，其是一个m*m的矩阵
        for i in range(self.m):
            self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)#计算核函数

#1.加载数据
def loadDataSet(filename):
    dataMat = []#添加数据
    labelMat = []#添加数据标签
    f = open(filename,encoding='UTF-8')
    #按行读取数据
    for line in f.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([ float(lineArr[0]), float(lineArr[1])])#添加常数1
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat

#2.计算核函数，简单来说就是原先有x_{i}x的地方都要换成核函数的内积形式即x_{i}x\Rightarrow 
def kernelTrans(X, A, kTup): #计算内核或将数据转换为高维空间
    m,n = np.shape(X)#m行
    K = np.mat(np.zeros((m,1)))#mat创建矩阵，A代表们每一行样本xi
    if kTup[0]=='lin': 
        K = X * A.T   #线性核函数,k[xi,x]=xi*x，核函数是K(x_{i},x)即拿来一个点x，要和所有样本x_{i}做运算
    elif kTup[0]=='rbf':
        for j in range(m):
            deltaRow = X[j,:] - A#每行样本数据减去一个常数(x-xi)
            K[j] = deltaRow*deltaRow.T
        K = np.exp(K/(-1*kTup[1]**2)) #NumPy中的除法是元素的而不是Matlab中的矩阵
    else:
        raise NameError('Houston We Have a Problem -- \That Kernel is not recognized')
    return K

#用来在计算完i和j的Ei和Ej后更新数据结构中的的eCache
def updateEkK(oS, k):#更改任何alpha值后，更新缓存中的新值。alpha决定了决策边界
    Ek = calcEkK(oS, k)
    oS.eCache[k] = [1,Ek]

#2.计算误差
def calcEkK(oS, k):
    fXk = float(np.multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T)) + oS.b #预测值
    Ek = fXk - float(oS.labelMat[k])#误差，Ei=yi*-yi
    return Ek

#第一次寻找j
def selectJrand(i,m):
    j=i #we want to select any J not equal to i
    while (j==i):
        j = int(np.random.uniform(0,m))
    return j
#采用启发式来寻找j
def selectJK(i, oS, Ei):         #这是第二个选择-启发式，calcs Ej
    maxK = -1; maxDeltaE = 0; Ej = 0#最大的标志位
    oS.eCache[i] = [1,Ei]  #设置标志位, #choose the alpha that gives the maximum delta E
    validEcacheList = np.nonzero(oS.eCache[:,0].A)[0]   #?
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:   #循环遍历有效的Ecache值，找到最大的E值
            if k == i: continue #don't calc for i, waste of time
            Ek = calcEkK(oS, k)#计算误差Ei
            deltaE = abs(Ei - Ek)
            #寻找最大的误差
            if (deltaE > maxDeltaE):
                maxK = k; maxDeltaE = deltaE; Ej = Ek
        return maxK, Ej
    else:   #在这种情况下(第一次)，我们没有任何有效的eCache值
        j = selectJrand(i, oS.m)
        Ej = calcEkK(oS, j)
    return j, Ej

#根据条件赛选符合约束条件的aj
def clipAlpha(aj,H,L):
    if aj > H: 
        aj = H
    if L > aj:
        aj = L
    return aj

#用来优化\alpha和b的核心代码,最简版本的smoSimple内循环（就是for循环下面的代码：
#用来优化\alpha和b的核心代码）一模一样
def innerLK(i, oS):
    Ei = calcEkK(oS, i)#计算出来的误差
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        j,Ej = selectJK(i, oS, Ei) #采用启发式寻找j
        alphaIold = oS.alphas[i].copy();
        alphaJold = oS.alphas[j].copy();
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H: print( "L==H"); return 0
        eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel，优化部分，将比之前
        if eta >= 0: print( "eta>=0"); return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        updateEkK(oS, j) #added this for the Ecache
        if (abs(oS.alphas[j] - alphaJold) < 0.00001): print ("j not moving enough"); return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
        updateEkK(oS, i) #added this for the Ecache                    
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
            oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): 
            oS.b = b2
        else:
            oS.b = (b1 + b2)/2.0
        return 1

    else:
        return 0

#循环迭代优化参数 ,这里的iter就是单纯的代表一次循环，而不管循环内部具体做了什么，它没有被清0这个过程，
#再来看一下内循环，这里对应着两种情况，一种是在全集上面遍历（[0,C]），另一种是非边界上面（（0，C）），通过
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)):    #full Platt SMO
    
    oS = optStructK(np.mat(dataMatIn),np.mat(classLabels).transpose(),C,toler, kTup)
    iter = 0
    entireSet = True; 
    alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:   #go over all(全集遍历)
            for i in range(oS.m):        
                alphaPairsChanged += innerLK(i,oS)
                print ("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        else:#go over non-bound (railed) alphas
            nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerLK(i,oS)
                print ("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        if entireSet: 
            entireSet = False #toggle entire set loop
        elif (alphaPairsChanged == 0): 
            entireSet = True  
        print ("iteration number: %d" % iter)
    return oS.b,oS.alphas

#这里主要作用就是使用了训练集去训练SVM模型，然后分别统计该模型在训练集上和测试集上的错误率
def testRbf(k1):
#    dataArr,labelArr = loadDataSet(data_train)#加载进来数据
    dataArr,labelArr = loadDataSet('testSetRBF.txt')#加载进来数据
    b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 计算循环迭代优化出来的a和b,K1代表松弛因子
    datMat=np.mat(dataArr); labelMat = np.mat(labelArr).transpose()
    svInd=np.nonzero(alphas.A>0)[0]#找出不为零
    sVs=datMat[svInd] #get matrix of only support vectors得到只有支持向量的矩阵
    labelSV = labelMat[svInd];
    print ("there are %d Support Vectors" % np.shape(sVs)[0])
    m,n = np.shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
        predict=kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b
        if np.sign(predict)!=np.sign(labelArr[i]): errorCount += 1
    print ("the training error rate is: %f" % (float(errorCount)/m))#训练数据打印错误率
    dataArr,labelArr = loadDataSet('testSetRBF2.txt')
    errorCount = 0
    datMat=np.mat(dataArr); labelMat = np.mat(labelArr).transpose()
    m,n = np.shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
        predict=kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b
        if np.sign(predict)!=np.sign(labelArr[i]): errorCount += 1    
    print ("the test error rate is: %f" % (float(errorCount)/m))#测试数据打印错误率
    
    return dataArr,labelArr,alphas

def showClassifer(dataMat,labelMat,alphas):
    data_plus = []                                  
    data_minus = []
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus)              
    data_minus_np = np.array(data_minus)            
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)   
    plt.scatter(np.transpose(data_minus_np)[0],np.transpose(data_minus_np)[1], s=30, alpha=0.7) 
    for i, alpha in enumerate(alphas):
        if abs(alpha) > 0:
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
    plt.show()
if __name__ == '__main__':
    dataArr,labelArr = loadDataSet('testSet.txt')
#    b, alphas = smoP(dataArr,labelArr,0.6 ,0.001,40)
#    print(dataArr)
#    print(labelArr)
    dataArr,labelArr,alphas=testRbf(1.3)
    showClassifer(dataArr,labelArr,alphas)