第2章 GAN初步:2.3 生成手写数字1
在2.2节中,我们进行了大量的工作来编写GAN的框架,并熟悉了它的使用。这意味着,当我们从生成简单的1010格式规律过渡到生成看起来像手写数字的图像时,所需的工作量相对减少了。
我们还是从一个架构图开始吧。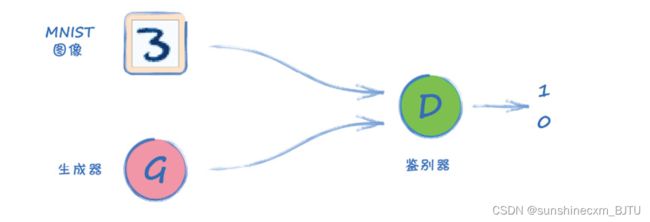
如图所示,总体的架构仍然保持不变。真实图像由我们在第1章中使用过的MNIST数据集提供。生成器的任务是生成相同大小的图像。随着训练的进展,我们希望生成的图像越来越真实,并可以骗过鉴别器。
在构建代码时,我们将复制之前构建MNIST分类器以及用于生成1010格式规律GAN的代码。
2.3.1 数据类
我们将使用torch.utils.data.Dataset从CSV文件源载入MNIST数据,它是PyTorch提供的类。我们可以直接复制之前创建的MnistDataset类,无须任何改变。
Dataset类将数据包装成张量。对于每个样本,它返回一个代表实际数字的标签、一个0~1的像素值,以及一个独热目标张量。
加载完成后,我们可以通过绘制样本图像,测试Dataset类是否可以正常工作。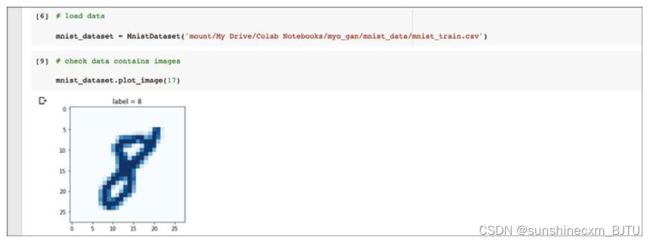
2.3.2 MNIST鉴别器
GAN里面的鉴别器是一个分类器。我们已经为MNIST图像构建了一个分类器。事实上,MNIST分类器的代码几乎与我们在1010 GAN中使用的完全相同。唯一的区别是神经网络的大小。
这里,我们可以复制2.2.2节中的鉴别器代码,只需要对神经网络层的大小作出调整即可。
鉴别器类中的其他部分保持不变,包括forward()、train()以及plot_progress()函数。
2.3.3 测试鉴别器
在构建生成器之前,我们先测试鉴别器,确保它至少能将真实图像与随机噪声区分开。由于我们在第1章已经构建了一个类似的神经网络用于数字图像分类,这个测试应该不成问题。
以下代码将使用60 000幅训练集中的真实图像,奖励鉴别器将训练数据判别为真,也就是输出1.0。
对于每个真实数据样本,我们使用generate_random(784)生成一幅由随机像素值组成的反例图像。我们训练鉴别器识别这些伪造数据,目标输出为0.0。
单元格上方的%%time指令帮助我们了解训练所需的时间,耗时应在2分30秒左右。
让我们绘制训练过程中的损失值变化。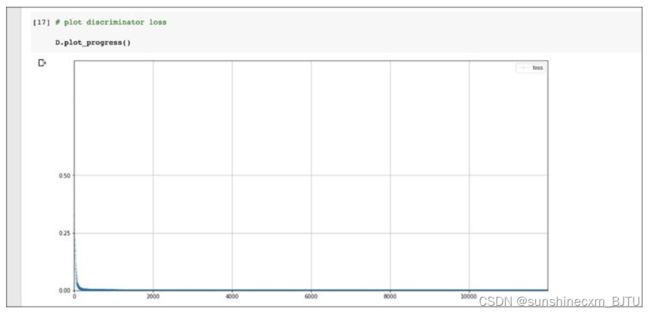
如上图所示,损失值下降并一直保持接近0的值,这正是我们希望达到的效果。
让我们随机选取一些训练集中的图像以及一些随机噪声图像,分别作为输入来测试训练后的鉴别器。
我们可以看到,输入真实的图像对应较高的输出值,说明鉴别器认为它们是真实的。同样地,输入随机噪声图像对应的输出值较低。
这证明鉴别器有能力从随机噪声图像中识别出真实图像。由于我们在第1章中已经证明了一个非常相似的网络可以将图像分成10类,因此这样的结果并不令人感到意外。
2.3.4 MNIST生成器
现在,让我们看一下更有趣的生成器。
我们需要生成器可以生成跟MNIST数据集中图像格式相同的、包含28×28=784像素的图像。
首先,我们将鉴别器的神经网络反转。反转后的网络的输出层有784个节点,隐含层有200个节点,输入层有1个节点。下图中并列显示了生成器网络和鉴别器网络。可以清楚地看到,生成器所输出的784个像素值正是鉴别器所期待的输入。
在之前的1010 GAN中,训练后的生成器可以生成符合1010格式规律的输出。这里,我们不希望每次的输出都相同,而希望它输出不同的、代表训练数据中所有数字的图像。例如,我们希望它生成的图像看起来像3、7、4、9等。
让我们思考一下要如何实现这一设想。我们知道,对于给定的输入,一个神经网络的输出是不变的。要知道,对于神经网络,只有训练是部分随机的,为给定的输入计算输出不是随机的。
这就需要我们改变生成器的输入,使它不再使用之前的常数0.5。我们在每个训练循环中,将一个随机值输入生成器。 我们更新架构图,加入这个随机种子(random seed)。
为什么将一个随机种子输入生成器,能帮助生成器生成不同的图像呢?
实际上,我们还不能确定其原因。但是,我们可以寄希望于生成器学习为不同的输入生成不同的输出。例如,它可能学到,对0.0~0.2的输入生成代表3的图像,或对0.4~0.6的输入生成代表9的图像等。
生成器的代码直接复制1010 GAN的生成器代码,只对神经网络层的大小做出改变。
2.3.5 检查生成器输出
在训练GAN之前,让我们检查一下生成器的输出格式是否正确。

我们创建一个新的生成器对象,并输入一个随机种子,即得到一个输出张量。我们可以通过utput.shape来确认该张量有784个值。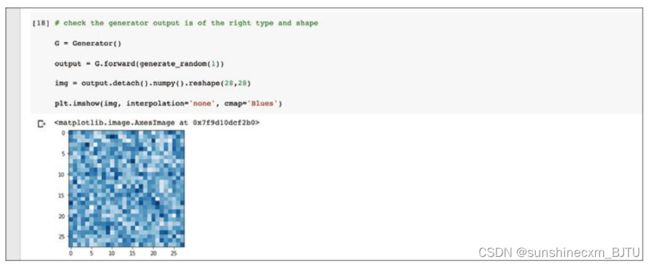
作为一幅图像,我们可以看到它是相当无规律的。这是因为生成器还没有经过训练。此时如果图像中出现任何图案,则意味着某个环节出错了。
2.3.6 训练GAN
让我们开始训练这个GAN。训练循环与2.2.6节所述一模一样,唯一不同的是鉴别器和生成器的输入数据。
训练需要几分钟。以我训练的情况为例,训练耗时4分钟多一点。计数器每隔10 000个训练样本打印一次,直到增加到120 000为止。这是因为鉴别器训练了60 000个MNIST图像和60 000个生成的图像。
让我们画出鉴别器在训练中的损失值。
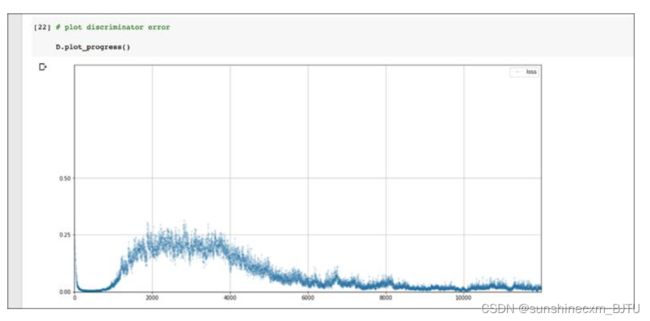
这是一幅有意思的图! 损失值先下降到0,并在一段时间内保持在较低水平,表明鉴别器领先于生成器。接着,损失值上升到略低于0.25的位置,这表明鉴别器和生成器旗鼓相当。不过,鉴别器随后再次发力,损失值下降并保持在较低水平。
回顾一下,理想的损失值应该在0.25左右,也就是鉴别器和生成器达到平衡。其中,鉴别器无法肯定地从生成的图像中区分真实图像。如果鉴别器的损失值趋近于0,表明该生成器没能学会骗过鉴别器。让我们再看看生成器的训练损失图。
起初,鉴别器能够正确识别生成的图像,这是损失值偏高的原因。接着,生成器和鉴别器达到一些平衡,损失值下降到0.25上方并保持一段时间。训练的后半部分,随着鉴别器再次超过生成器,损失值再度升高。
接着,让我们看一下生成器输出的图像。这么做不只是为了有趣,而是为了从中发现有用的信息。
由于不同的随机种子应当生成不同的图像,所以我们绘制多幅输出图像并查看。
这段代码使用matplotlib的功能,创建一个包含多幅图像的网格。这里创建的是3×2的网格,包含6幅生成图像。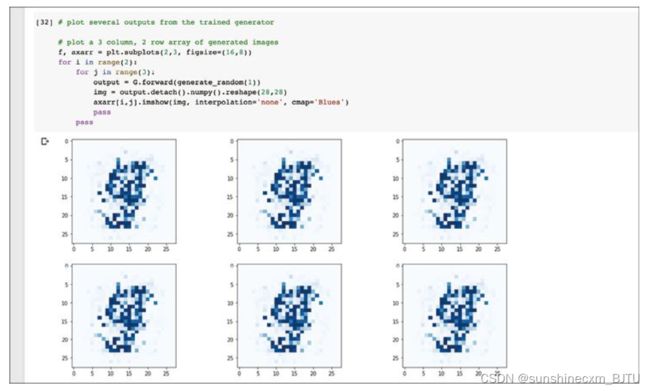
我们首先注意到,生成的图像不是随机噪声,而是有某种形状。图像中间有较暗的区域,与真实的手写数字图像很像,这很好。更妙的是,这些图像看起来确实像某个数字。我觉得图像是9,不过有读者也可能认为是5。
即使图中显示的数字并不完美,这仍是一个不错的开端。我们用相对简单的代码实现了一个重要的里程碑。要记住,生成器并没有直接看过MNIST数据集中的图像,但是它已经学会了创建类似的图像。 这些图像不是随机噪声,而是几乎可被识别的手写数字。