Python学习之第五次作业

Python学习之第五次作业

图表的绘制

在实现直方图的绘制之前，学习了普通线图、折线图、子图、饼图以及散点图的绘制。
import numpy as np
import matplotlib.pyplot as plt

1、普通线图：

x = np.linspace(-5,5,50) # numpy数组生成（-5，5)的50个数字
y1 = 4*x + 1  # 定义y1方程
y2 = x**2 -5  # 定义y2方程
plt.plot(x,y1) # y1
plt.plot(x,y2) # y2
plt.show()

2、折线图：

plt.plot(x1,y1,label='Slight Line') 
#从左到右的参数依次是横坐标、纵坐标、标签、线宽、线的颜色、需不需要标出点（默认不标），点的颜色，点的大小
plt.plot(x2,y2,label='Point  Line',linewidth=3,color='r',marker='^',markerfacecolor='yellow',markersize=10) 

3、子图：

t = np.linspace(-5, 5, 50)   #numpy数组生成50个数字
s1 = np.sin(np.pi*t)
s2 = np.sin(np.pi*t)
plt.figure(1)
plt.subplot(211)  #设置子图
plt.plot(t, s1)
plt.subplot(212)
plt.plot(t, 2*s1)
plt.show()

4、饼图：

labels = 'Type 1', 'Type 2', 'Type 3', 'Type 4'
sizes = [10,20, 30, 40]
explode = (0, 0.1, 0, 0)  # 分离  explode=explode,
fig1, ax1 = plt.subplots()
ax1.pie(sizes,labels=labels,autopct='%1.0f%%',startangle=90)
ax1.axis('equal') # 相等的长宽比可以将饼图置位圆形
plt.show()

5、散点图：

# 散点图
x = np.random.random(30) 
y = np.random.random(30)
colors = np.random.random(30) # 随机生成颜色  
area = (50*np.random.random(30))  # s=area
plt.scatter(x, y) # 参数实现 c=colors
plt.show()

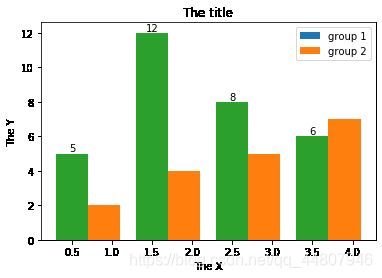
6、直方图：

代码如下：

import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
List1 = [2,4,5,7]
List2 = [5,12,8,6]
Width = 0.8
n =2
width = Width/2#长条形的宽度
plt.bar([0.5,1.5,2.5,3.5],[5,12,8,6],width = width,label = 'group 1')
plt.bar([0.9,1.9,2.9,3.9],[2,4,5,7],width = width,label = 'group 2')
rects = plt.bar([0.5,1.5,2.5,3.5],[5,12,8,6], width=0.4) 
#rects = plt.bar([0.5,1.5,2.5,3.5],[2,4,5,7], width=0.4 , label="1") 
for rect in rects:#在柱形图上显示数据
    height = rect.get_height()
    plt.text(rect.get_x()+rect.get_width()/2,height,str(height),ha = 'center',va = 'bottom')
plt.xlabel('The X')#X轴名称
plt.ylabel('The Y')#Y轴名称
plt.title('The title')#直方图名称
plt.legend()#给图加上图例
plt.show()

在直方图上添加数据标签：（标签的横坐标，标签的纵坐标，标签显示，垂直对齐方式，水平对齐方式）

画出的直方图：

代码注释

import numpy as np
import matplotlib.pyplot as plt
p_x = np.array([[3, 3], [4, 3], [1, 1], [2.5, 3]])#输入四个点(3,3),(4,3),(1,1),(2.5,3)
y = np.array([1, 1, -1, -1])
for i in range(len(p_x)):#绘制初始点
	if y[i] == 1:
		plt.plot(p_x[i][0], p_x[i][1], 'ro')#红色圆点
	else:
		plt.plot(p_x[i][0], p_x[i][1], 'bo')#蓝色圆点
w = np.array([1, 0])#权值
b = 0#偏导
delta = 1#学习率
for i in range(100):
	temp = -1
	for i in range(len(p_x)):
		if y[j] !* np.sign(npsot(w, p_x[0]) + b):
			temp = j
			break
		if temp == -1:#三个点都被正确分类
			break
		w += delta * y[temp] * p_x[temp]
		b += delta * y[temp]
line_x = [0, 10]#x轴的范围为0~10
line_y= [0, 0]
for i in range(len(line_x)):#超平面表达式为wx+b=0,其中w为向量w1x1+w2x2+b=0,x2=(-w1x1-b)/w2
	line_y[i] = (-w[0] * line_x[i] - b) / w[1]
plt.plot(line_x, line_y)
plt.grid(True)# 显示背景的网格线
plt.show()

感知机工作原理

感知机是二分类的线性分类模型，属于监督学习算法。感知机导入了基于误分类的损失函数，利用梯度下降法对损失函数进行最优化求解。
学习了一下下面的博客，对感知机工作原理有了更深入的理解，在输入时，对于不同输入的不同影响，其权重也不一样：
https://www.cnblogs.com/huangyc/p/9706575.html

Linux安装

对于Linux的安装，我参考了下面的博客：
https://www.cnblogs.com/huangyc/p/9706575.html