【数据挖掘】时间序列分析理论和使用SPSS进行ARIMA模型分析
【数据挖掘】时间序列分析理论和使用SPSS进行ARIMA模型分析
- 1 前言
-
- 1.1 基本概念
- 1.2 时间序列分析的一般步骤
- 1.3 时间序列的图形化观察及检验
- 2 时间序列的图形化观察工具
-
- 2.1 序列图
- 2.2 直方图
- 2.3 自相关函数图和偏自相关函数图
- 2.4 谱密度图(Spectral)
- 2.5 互相关图(Cross correlation)
- 3 时间序列的检验方法
-
- 3.1 参数检验法
- 3.2 游程检验法
- 4 时间序列分析应用举例
-
- 4.1 图形化观察
- 4.2 时间序列预处理
- 5 ARIMA模型分析
-
- 5.1 ARIMA(p,d,q)模型
- 5.2 ARIMA(p,d,q)(P,D,Q)^s模型
- 5.3 ARIMA应用举例
-
- (1)确定工具
- (2)导入数据
- (4)平稳性分析
- (5)构建ARIMA模型
- (6)输出结果
- 后续
1 前言
1.1 基本概念
时间序列分析(Time Series Analysis)是研究事物发展变化规律的一种量化分析方法,隶属于统计学但又不同于其他统计分析方法的特殊特点。对于时间序列可以有不同层次的理解,一般情况下,那些依据时间先后顺序排列起来的一系列有相同内涵的数据都可以称为时间序列。
实际上,只要能够被持续地观察和度量,同时被记录,就能得到所谓的时间序列。这一点对于我们测绘的太熟悉不过了,变形监测的沉降数据、卫星的周期观测数据等等都属于时间序列数据。
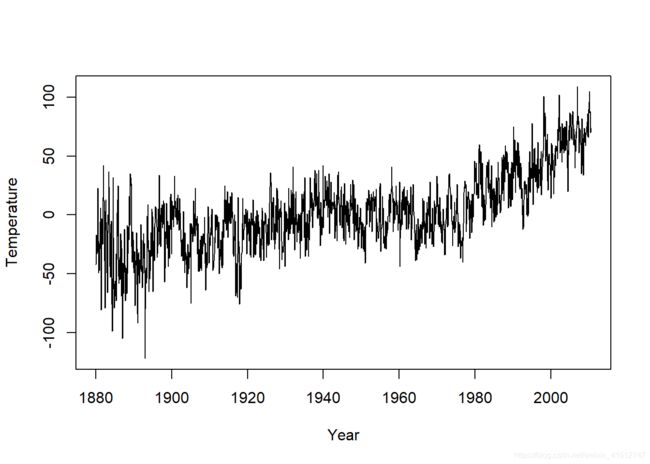
(图片来源: 线性时间序列案例学习—全球温度异常值)
指标集 是指可以直观理解为时间t的取值范围,对一般的随机过程来说它是一个连续变化的范围。
采样间隔 意思是时间序列中相邻两个数的时间间隔。在实际研究中,在整个数据期间一般都取一致的时间间隔,这样会使分析结果更具直观意义,易令人信服。
平稳随机过程 在一些时间序列分析方法当中要求时间序列具有平稳性,即要求时间序列对应的随机过程是一个平稳的随机过程。
白噪声序列 白噪声序列是一种特殊的平稳序列,它定义为:若堆积序列{yt}由互补相关的随机变量构成,即对所有s≠t,Cov(ys,yt)=0,则称其为白噪声序列。可以看出,白噪声序列是一种平稳序列,在不同时点上的随机变量的协方差为0,。该特性通常被称为“无记忆性”,意味着人们无法根据过去的特点推测其未来的走向,其变化没有规律可循。虽然有这个特性,但是白噪声序列是其他时间序列产生的基石,这在时间序列ARIMA模型分析中体现得相当明显。另外,时间序列分析中,当模型的残差序列称为白噪声序列时,可认为模型达到了较好的效果,剩余残差中已经没有可以识别的信息。因此,白噪声序列对模型检验也是很有用处的。
时点序列和时期序列 实际之中,人们研究的时间序列是前面提到的随机过程的一个“实现”,也就是那些按时间先后顺序排列的一系列数据。这些数据往往由两部分组成:一是观测值;二是观测值对应的时间点或时间段。
1.2 时间序列分析的一般步骤
(1)数据的准备阶段
(2)数据的观察及检验阶段
(3)数据的预处理阶段
(4)数据分析和建模阶段
(5)模型的评价阶段
对于(4):谱分析方法适用于那些高频波动数据,通过对序列中各种周期成分的识别来达到模型识别、随机性波动检验、趋势性识别等目的。
对于(5):模型评价应于模型分析的目标相结合,与研究目的相结合。预测是时间序列分析的重要目标之一。预测是时间序列分析的重要目标之一。预测精度无疑是衡量模型好坏的重要指标。预测精度的衡量指标包括误差平方和SSE、平均绝对百分误差MAPE,拟合优度R方,预测值的方差,等等。
时间序列的横向关系是时间序列分析的另一重要目标。对此模型中变量的相关性也是考察的重点。模型的F统计值、各个变量系数t、AIC、SBC等统计量都是参考的重要依据。
在时间序列的回归分析当中,控制往往也是分析的目标之一。对此考察变量间准确而非虚假的因果数量关系也是模型评价的重点。模型中的系数不但要通过显著性检验,还必须有一定的实际意义,这就涉及模型估计方法的选择问题。
(6)模型的实施应用阶段
1.3 时间序列的图形化观察及检验
通过图形化观察能够把握时间序列的诸多特征,如时间序列的发展趋势是上升还是下降,还是没有规律的上下波动;时间序列的变化的周期性特点;时间序列波动幅度的变化规律;时间序列中是否存在异常点,时间序列不同时间点上数据的关系等。
主要有以下几个方面:
(1)时间序列的正态性
(2)时间序列的平稳性
(3)时间序列的周期性
(4)时间序列其他特性
2 时间序列的图形化观察工具
2.1 序列图
序列图是按照时点顺序将数据展现出来的一种图形,它是时间序列分析当中用的最多也是最为有用的图形工具,可用于对序列直观特性的观察。
一个平稳的时间序列,由于各时间点的统计特性保持不变,或者各时间点的协方差只与时间间隔有关而与时间起点无关,因此在图形表现上:在水平方向平稳发展,在垂直方向的波动性保持稳定,如下图所示。
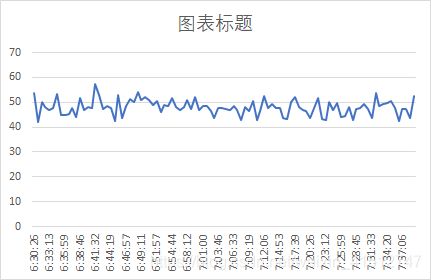
实践中,真正具有平稳性的时间序列并不多见,同城都会表现出非平稳性。非平稳性的表现形式多种多样,主要特征有趋势性、异方差性、波动性、周期性、季节性,以及这些特征的交错呈现。
“簇集性”是指数据在一段时间内具有相似的水平。在不同的水平间呈跳跃式变化,而非平稳性变化。
2.2 直方图
直方图是体现序列数据分布特征的一种图形,通过直方图可以了解序列的平稳性、正态性等特征。
2.3 自相关函数图和偏自相关函数图
对识别时间序列的各种非平稳性和确定时序模型中参数有非常重要的作用。所谓自相关是指序列与其自身经过某些阶数之后形成的序列之间 存在某种程度的相关性。

严格的相关性检验还需要根据相关函数值的统计性质,构造统计量进行假设检验。其令假设是:某阶相关函数值 与0无显著差异。只通过检验拒绝了零假设,才可以认为序列与该阶之后序列存在着显著的相关性,意味着在某种程度上序列的当前状态可以由序列过去的变化进行解释。
应该注意的是,对序列在两个时期间的相关性考察时应剔除那些外来因素的影响。例如,序列与其一阶滞后序列的相关性可能影响到它与二阶滞后序列的相关性。因此要考察后者,就要剔除前者带来的影响。偏自相关函数就是在其他序列情况下的两条序列条件相关性的度量函数。
各种非平稳的特性在两图中会有不同的表现,不过在实际应用中需要注意的一点事,有相关图的形式并不能唯一地确定序列的特征,因此在实际建模是要将统计量的检验和图形结合起来进行模式识别。
2.4 谱密度图(Spectral)
谱密度图用于序列周期性的检验,它是时间序列频域分析中识别序列隐含周期性的有效方法。
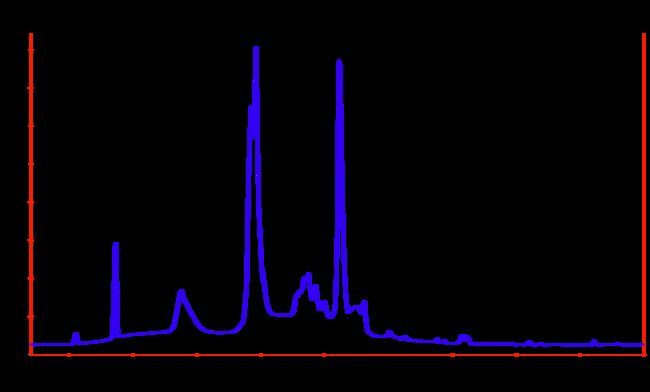
(图片来源: link.)
时间序列的频域分析认为时间序列是具有不同周期的谐波叠加而成的。如果将那些没有周期的序列看作是周期无限长的序列,则这种观点可以覆盖所有的时间序列。基于这种观点的谱分析法重在对序列当中的周期成分进行识别,从而达到对序列进行认识和分解的目的。
2.5 互相关图(Cross correlation)
互相关图是对两个互相对应的时间序列进行相关性分析的使用图形工具,互相关图是依据互相关函数绘制出来的,互相关函数与自相关函数的原理相同,差别之处在于它所体现的是不同时间序列间不同时期滞后序列的相关性。
3 时间序列的检验方法
3.1 参数检验法
平稳性的参数检验法从序列的宽平稳性出发,检验序列的均值、方差、相关函数等数字特征是否随时间的推移而变化。
3.2 游程检验法
4 时间序列分析应用举例
4.1 图形化观察
(1)绘制序列图
(2)绘制自相关函数图和偏自相关函数图
(3)绘制互相关图
4.2 时间序列预处理
(1)序列缺失数据的替换处理
(2)序列数据的变换处理:序列的平稳化处理;序列的平滑处理
时间序列中应用游程检验的基本思路是,将序列的数值按一定规则重新分组形成两类。游程则为时间序列中同类数据连载一起的子序列个数。
5 ARIMA模型分析
ARIMA模型(Autoregressive Integrated Moving Average model)自回归移动平均结合模型,又称整合平均自回归模型,是时间预测分析方法之一。
ARIMA(p,d,q)中,AR是自回归,p是自回归系数;MA为滑动平均,q为滑动平均项数,d为使之成为平稳序列所做的差分次数(阶数)。
5.1 ARIMA(p,d,q)模型
当序列同时存在趋势性时,可通过某些阶数的差分处理使序列平稳化,这样的序列是一种准平稳的序列。对这种准平稳序列的分析应采用ARIMA(p,d,q)模型,其中d表示平稳化过程中的差分阶段。
5.2 ARIMA(p,d,q)(P,D,Q)^s模型
当序列同时存在趋势性和季节性时,序列具有以季节周期的整数倍为长度的相关性,需要经过某些阶段的逐期差分和季节差分才能使序列平稳化。对这种平稳序列的分析应采用本模型,其中P、Q为季节性的自回归和移动平均阶数,D为季节差分阶数,s为季节周期。
5.3 ARIMA应用举例
(1)确定工具
自己使用的是SPSS 25;选择数据:项目过程中的一个数据(某一段时间内雾的浓度)。
(2)导入数据
(3)图像化观察
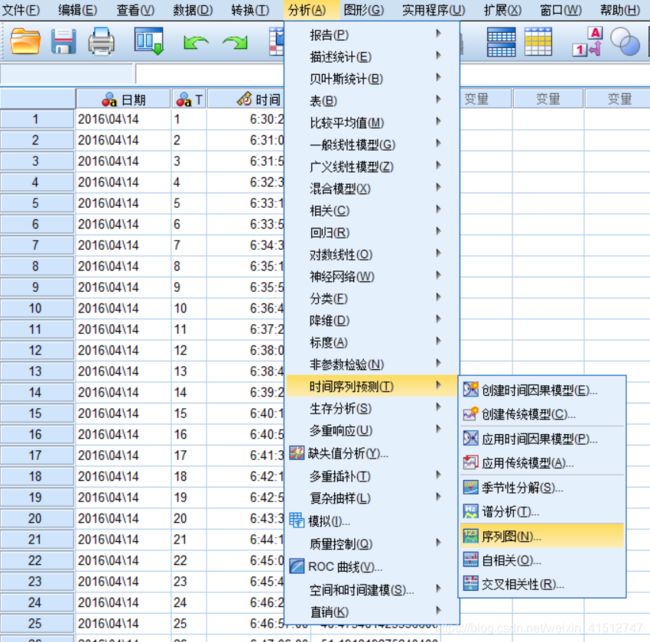
选择要显示的变量,此处是V4,时间轴标签选定“时间”一列,点击确定得到序列图。
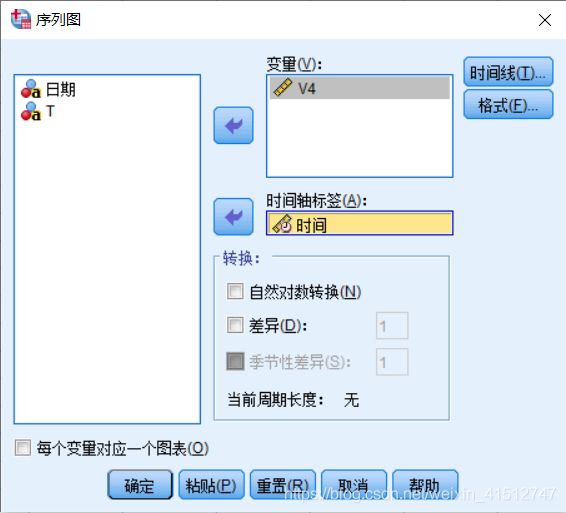
序列图如下所示:
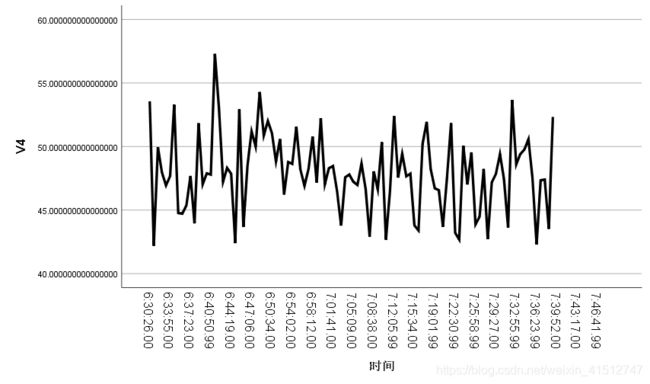
因为这是一天某一时间段的变化,序列图显示不可能存在季节性变化,故不需要进行季节性分解。
(4)平稳性分析
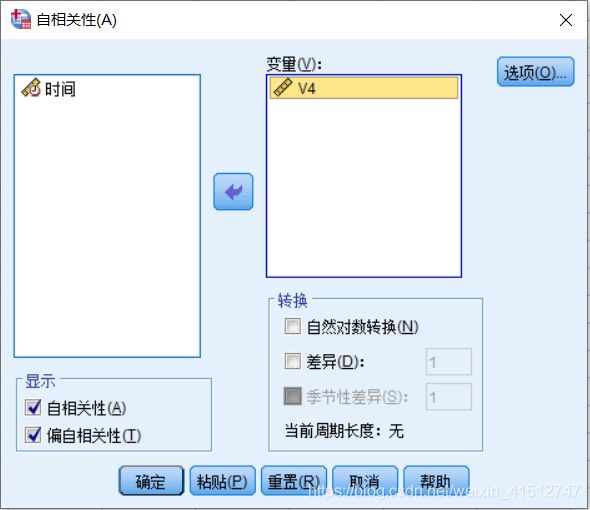
ARIMA模型要求序列是平稳序列,因此要对数据进行平稳性分析。下面做大雾浓度序列的自相关图和偏自相关图。
选择“大雾浓度V4”为变量,勾选“自相关”,“偏自相关”。
自相关图:

偏自相关图:

从图中可以看出,序列的自相关图(ACF)和偏自相关图(偏ACF)大部分编号位于置信区间内部,说明序列是基本平稳的。
(5)构建ARIMA模型
在【分析】中选择【时间序列预测】,选择【创建传统模型】。
在【变量】页面,选择方法:ARIMA;由上述ACF和PACF选定条件,p=10,d=0,q=10。
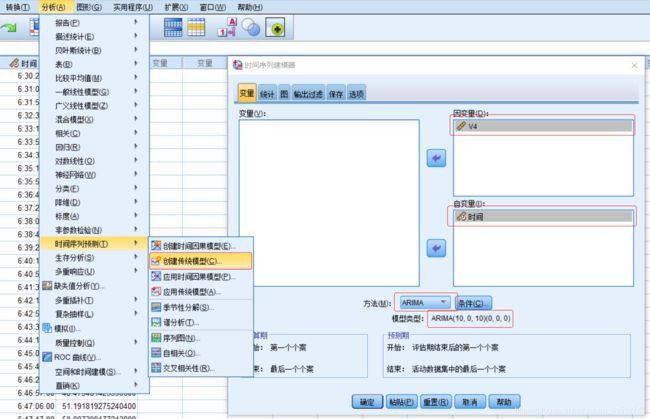
在【统计】页面,根据自己需要勾选显示的数据;
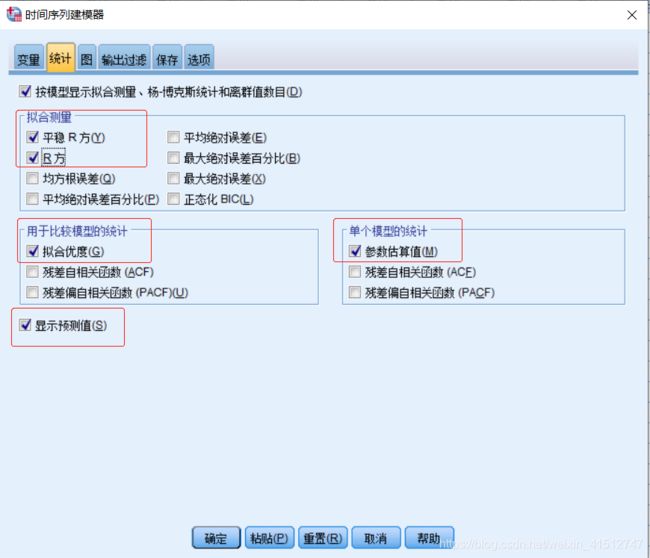
在【图】页面,选自自己需要输出的图形数据;

在【保存】页面,勾选自己需要保存的内容。

(6)输出结果
点击确定,软件输出结果。

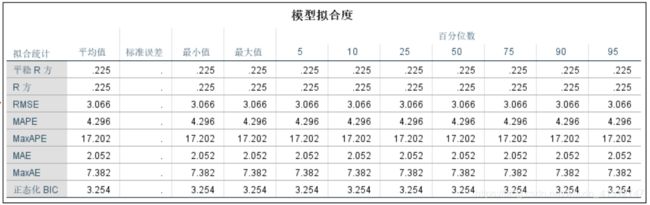
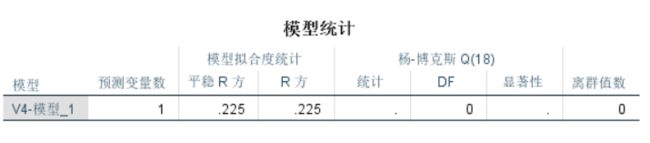
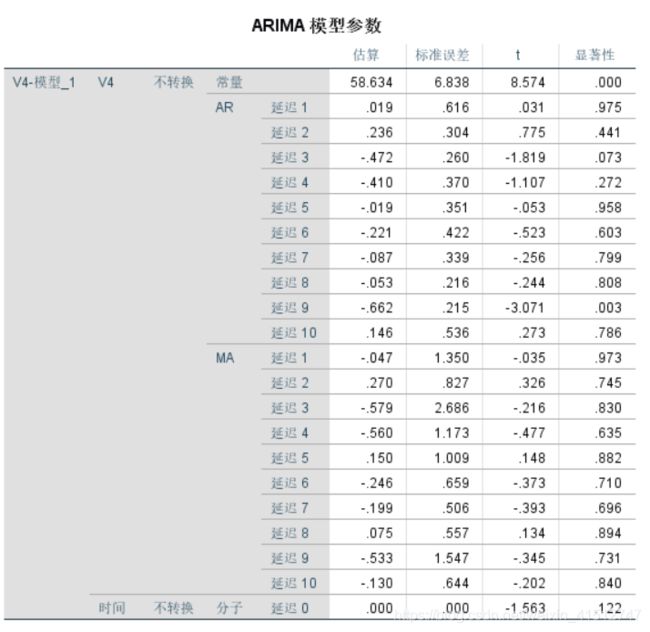
此处AR系数显著为0,R方式0.225,说明参数选择不太好,需要进一步做调整;
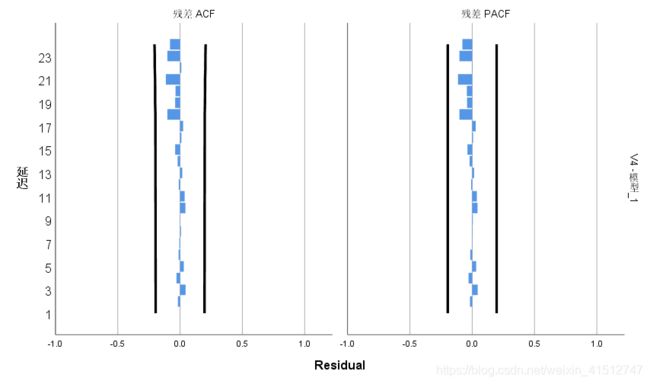
残差的ACF和PACF图,都落在置信范围内。

根据选定的参数,得到的拟合预测图,大致看起来还算可以,但是有待进一步的优化。
后续
至此,时间序列分析理论和其中具有代表性的ARIMA分析结束,部分观点来自百度经验、《SPSS统计分析方法及应用》(薛薇 著)。
有哪些地方写得不准确的地方还望大家能够及时指出,期待与各位一起交流、共同进步。