NeRF神经辐射场学习笔记（三）——Point-NeRF论文解读

声明

本人书写本系列博客目的是为了记录我学习三维重建领域相关知识的过程和心得，不涉及任何商业意图，欢迎互相交流，批评指正。

论文概述

Point-NeRF结合了NeRF利用体素渲染合成高质量视图的方法，以及MVS中通过卷积神经网络快速重建场景的思路，先通过MVSNet得到初始神经点云场景，然后利用神经3D点云和神经特征来构建一个基于Point的辐射场，来渲染场景；在速度上面，其重建的时间要比NeRF提高了30倍。

Point-NeRF Representation

传统NeRF的体素渲染和辐射场方法

基于物理的体素渲染可以通过沿着可微光线（differentiable ray matching）计算来预测结果，即一个像素的渲染结果（颜色和不透明度）可以通过以下公式来计算：
$$\begin{gathered} c=\sum _M{\tau }_j(1-exp(-{\sigma }_j{\Delta }_j))r_j \\ {\tau }_j=exp(-\sum _{t=1}^{j-1}{\sigma }_t{\Delta }_t) \end{gathered}$$其中$\tau$表示体积透过率（volume transmittance），${\sigma }_j$和$r_j$分别表示射线上每个点$x_j$的体密度（不透明度）和颜色（辐射度），$\Delta$表示相邻采样点的距离差；
一个辐射场的作用是利用每个点的3D坐标和方向信息来表示该点的不透明度$\sigma$和颜色$r$，而NeRF则是用一个MLP网络结构来回归这种辐射场；本文则提出了新的观点，利用Point-NeRF——使用神经点云（a neural point cloud）来计算体积要素，使得拥有更快、更高质量的渲染结果。

基于Point的辐射场方法

首先定义一个点云：$P=(p_i,f_i,{\gamma }_i)|i=1,\dots ,N$，其中每个点$i$位于$p_i$处，并且与编码了局部场景信息的神经特征向量$f_i$（a neural feature vector that encodes the local scene content）相关联。并且为每个点配置了一个尺度置信值${\gamma }_i\in [0,1]$（a scale confidence value），用来表示一个点有多大的可能性位于实际的场景表面。而文章就将要利用该点云来回归一个辐射场；
给定任意的3D位置x，查询其周围在一定半径R内的K个邻近神经点；基于Point的辐射场可以抽象为一个神经模块（a neural module）——任意点沿任意方向从邻近点回归出的体密度$\sigma$和基于视觉的辐射度$r$：$$(\sigma ,r)=\text{Point-NeRF}(x,d,p_1,f_1,{\gamma }_1,\dots ,p_K,f_K,{\gamma }_K)$$
文章采用了类似于PointNet的，拥有多个子MLP的神经网络来做回归，即首先对每个神经点进行处理，然后将多点信息进行聚合，得到最终的预测值。具体网络结构如图所示：

1.逐点处理（Per-point processing）

文章用一个MLP $F$来处理每个邻近的神经电，用以预测$x$处的一个新的特征向量：
$$f_{i,x}=F(f_i,x-p_i)$$本质上来讲，原始特征$f_i$围绕$p_i$对局部3D场景内容进行编码，该MLP网络表示一个局部3D函数，该函数在$x$处输出特定的神经场景描述（the specific neural scene description）$f_{i,x}$，该描述由其局部帧中的神经点建模。 相对位置$x-p$的使用令网络不变量对点的平移具有更好的泛化作用。

2.基于视觉的辐射度回归（View-dependent radiance regression）

首先利用标准的逆距离加权（standard inverse distance weighting）来聚合从$F$中回归得到的$f_{i,x}$,以此来得到一个用来描述x处场景表示的简单特征值$f_x$：$$f_x=\sum _i{\gamma }_i\frac{w_i}{\sum w_i}{f}_{i,x},\text{其中}{w}_i=\frac{1}{||p_i-x||}$$紧接着，定义一个MLP $R$，用来从给定观测方向d回归r：$$r=R(f_x,d)$$逆距离加权被广泛应用于稀疏数据的插值，文章使用它来聚合神经特征，使得更近的神经点为渲染计算贡献更多；

3.体密度回归（Density regression）

同理，运用逆距离加权方式和定义的MLP $T$来计算$\sigma$：
$$\begin{gathered} {\sigma }_i=T(f_{i,x}) \\ \sigma =\sum _i{\sigma }_i{\gamma }_i\frac{w_i}{\sum w_i},w_i=\frac{1}{||p_i-x||} \end{gathered}$$如此一来，每个神经点直接对体密度作出贡献，置信度也显式地与贡献关联，这一点在后续的除点操作中很有用。

Point-NeRF Reconstruction

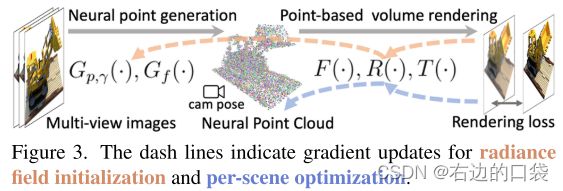
具体的基于Point-NeRF三维重建分为两大步骤：生成初始神经点云和基于Point的体素渲染逐帧优化；其主要的思路就是先利用MVSNet方法快速得到一个初始点云，然后在基于Point的辐射场上对点云进行进一步的渲染，而渲染的流程和理论分析在上一小节已经表明，但是来自外部重建方法所得到的初始点云通常会包含降低渲染质量的空洞河离群点，所以作者又提出了两种能够提升渲染效果和质量的方法；

生成基于Point的初始辐射场（Generating initial point-based radiance fields）

1.获取点的位置与置信度

对于位于点q的带有相机参数${\Phi }_q$的输入图像$I_q$，文章中运用MVSNet网络的多步操作处理得到了每个视角q下的点云$\{p_1,\dots ,p_{N_q}\}$，以及位于每个点$p_i$的置信度${\gamma }_i$：$$\{p_i,{\gamma }_i\}=G_{p,\gamma }(I_q,{\Phi }_q,I_{q_1},{\Phi }_{q_1},I_{q_2},{\Phi }_{q_2},\dots )$$其中$G_{p,\gamma }$是基于MVSNet网络的，$I_{q_n}$和${\Phi }_{q_n}$是MVS重建过程中使用的图片的邻域帧，一般两个就足够。

we follow MVSNet to first build a plane-swept cost volume by warping 2D image features from neighboring viewpoints and then regress depth probability volume using deep 3D CNNs. A depth map is computed by linearly combining per-plane depth values weighted by the probabilities. We unprojected the depth map to 3D space to get a point cloud $\{p_1,\dots ,p_{N_q}\}$ per view $q$.
Since the depth probabilities describe the likelihood of the point being on the surface, we tri-linearly sample the depth probability volume to obtain the point confidence ${\gamma }_i$ at each point $p_i$.

2.获取点的特征信息

文章采用带有3个下采样层的VGG网络 $G_f$来从每个图像$I_q$中提取特征图：$$\{f_i\}=G_f(I_q)$$

优化基于Point体素渲染效果的两种方法（Optimizing point-based radiance fields）

1.Point pruning

点置信度${\gamma }_i$表明了神经点是否靠近场景表面，所以文章利用这些置信度来prune不必要的离群值；根据体密度回归的公式定义以及逆距离加权的运用使得神经点的距离与渲染计算贡献相关联，故低置信度反映了一个点的局部区域的低体密度，即表明它是空的。 因此，每10k次迭代就prune ${\gamma }_i<0.1$的点。下图为有无Point pruning和Point growing两种方法所带来的效果展示：

同时文章还用置信度定义了一种稀疏损失函数，该损失函数会在优化的过程中强制置信度值接近0或1：$${\mathcal{L}}_{sparse}=\frac{1}{\gamma }\sum _{{\gamma }_i}[log({\gamma }_i)+log(1-{\gamma }_i)]$$

2.Point growing

该方法是用来生成新的点来覆盖原始点云中缺失的场景，即在射线采样的过程中利用NeRF所提出的公式来识别不透明度最高的点$x_{j_g}$，（其中${\alpha }_j=1-exp(-{\sigma }_j{\Delta }_j),j_g={\mathrm{argmax}}_j{\alpha }_j$），如果${\alpha }_{j_g}>T_{opacity}$并且${ϵ}_{j_g}>T_{dist}$（${ϵ}_{j_g}$是$x_{j_g}$到其最近的神经点的距离），则grow一个新的神经点，这意味着该位置位于表面附近，但远离其他神经点。通过重复这种grow策略，我们的辐射场可以扩展到覆盖初始点云中缺失的区域。下图表明即使在只有1000个初始点的极端情况下，该grow技术也能够逐步生成新的点并合理地覆盖物体表面：

损失函数定义

$${\mathcal{L}}_{opt}={\mathcal{L}}_{render}+a{\mathcal{L}}_{sparse}$$其中${\mathcal{L}}_{render}$是渲染过程中的损失函数，$a$取$2e^{-3}$。

参考文献和资料

[1]:【论文精读】Point-NeRF:Point-based Neural Radiance Fields
[2]:论文阅读笔记—CVPR2022—Point-NeRF
[3]:Point-NeRF: Point-based Neural Radiance Fields