线性回归模型的从零开始 || 深度学习 || Pytorch ||动手学深度学习08 || 跟李沐学AI

莫愁前路无知己, 天下谁人不识君？　　　　　——高适

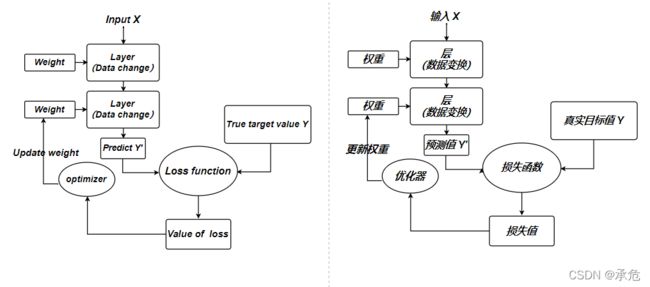
• 本文是对于跟李沐学AI——动手学深度学习第8节：线性回归的从零开始的代码实现、从生成数据集到模型参数的初始化、从创建数据迭代器到定义线性回归模型、损失函数与优化函数、最后根据设置的迭代轮次对模型进行训练、这是完整且标准的深度学习思想与过程的体现

• 线性回归作为最基础的机器学习模型、在机器学习库Sklearn 、统计模型库Statsmodels 以及众多深度学习库中都可以方便且快速地实现、而从零开始实现的意义在于 加深对深度学习模型的理解、更为直观地 体会模型的训练过程是如何进行的

%matplotlib inline
import random
import torch
from d2l import torch as d2l

• 生成人工数据集
• 特征数据 X 是由传入的样本量大小 num_examples 与权重向量 w 的长度来生成的、服从均值为0、方差为1的正态分布的随机数
• 另外还需要给标签数据 y 增加一部分随机误差来作为噪音干扰

def synthetic_data(w, b, num_examples):     # 传入系数、常数项和样本量
    
    X = torch.normal(0, 1, size=(num_examples, len(w)))  # 生成自变量数据
    y = torch.matmul(X, w) + b              # 令数据与权重相乘后相加、得到的结果再与偏差相加
    
    # 增加随机误差项作为噪音干扰
    y += torch.normal(0, 0.01, size=y.shape)   # 要用.shape、而不是len( )
    
    return X, y.reshape((-1, 1))            # 注意将标签数据转为所谓的列向量、实际上是二维张量
# 设置真实的权重向量与偏差
true_w, true_b = torch.tensor([3.0, -2.4]), torch.tensor([2.4])
# 调用函数synthetic_data来生成数据
features, label = synthetic_data(true_w, true_b, num_examples=1000)

• 查看生成数据与标签

print('features: ', features[0], '\nlabel   : ', label[0])

features:  tensor([0.2203, 0.4052]) 
label   :  tensor([2.0868])

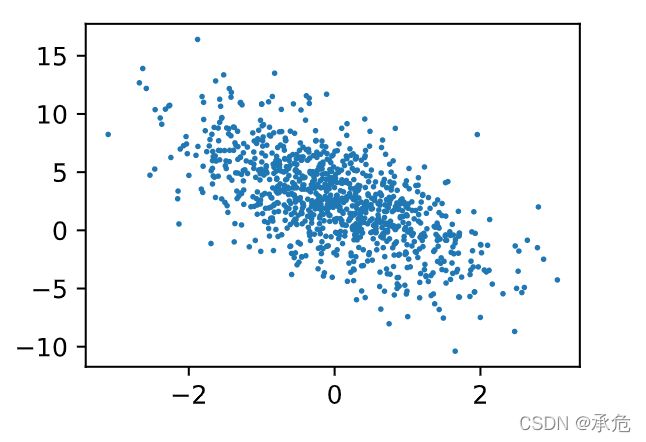
• 绘制第二个变量和因变量的散点图、查看两者之间的线性关系如何

d2l.set_figsize()
d2l.plt.scatter(features[:, 1].numpy(), label.numpy(), s=1.5);
# 可能会使用到.detach( )函数才可以将Torch张量改为Numpy数组

• 定义 数据迭代器 函数、向其传入批量大小、特征矩阵和标签向量
• 通过循环语句来从该函数中每次拿到特征数据和标签中的一小部分、即 小批量、当传入的数据全都被依次返回后、即完成了对模型的一轮迭代

def data_iter(batch_size, features, label):  # 出入批量大小、特征与标签
    
    num_examples = len(features)     # 得到样本量
    indices = list(range(num_examples))  # 相当于得到样本的索引
    
    # 将得到的索引打乱顺序、进而实现对小批量的随机抽取
    random.shuffle(indices)    # 这时的indices顺序已经被打乱
    
    for i in range(0, num_examples, batch_size):   # 在样本中跨过小批量的大小抽取
        
        # 得到小批量的索引、由于已经打乱了顺序、所以这就是对样本的随机抽取
        # 注意使用最小值函数、因为可能会在数据尽头无法满足批量的大小
        batch_indices = torch.tensor(           
                      indices[i: min(i + batch_size, num_examples)]) 
        # 相当于return、不过会保存这次提取的位置、下次循环从batch_size这个位置开始
        yield features[batch_indices], label[batch_indices]
# 将批量大小设置为10、尝试从数据迭代器中拿到一次数据
batch_size = 10
for X, y in data_iter(batch_size, features, label):
    print(X, '\n', y)
    break

tensor([[ 0.4318,  0.1997],
        [-0.7234, -0.0113],
        [ 0.6357,  0.9459],
        [-1.0930, -1.8608],
        [-1.8943,  0.2650],
        [ 1.2493, -0.9300],
        [-1.6498, -0.1448],
        [-0.8304,  0.4570],
        [ 0.8871,  1.2403],
        [-2.2990,  0.6360]]) 
 tensor([[ 3.2165],
        [ 0.2484],
        [ 2.0329],
        [ 3.5902],
        [-3.9199],
        [ 8.3903],
        [-2.2030],
        [-1.1903],
        [ 2.0963],
        [-6.0173]])

• 初始化模型参数、需要给出迭代的初始值、一般应尽可能地小
• 这里的模型参数 w 和 b 是不同于上面定义的 true_w 和 true_b的、w 和 b 是向模型中传入并不断根据求得的 梯度 来更新的、 true_w 和 true_b 是用来生成数据的
• 模型训练完成后、如果效果很好、那么 w 和 true_w 、b 和 true_b 都应该是非常接近的

# 回归系数服从均值为0、方差为0.1且形状为2行1列
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
# 回归常数取0即可
b = torch.zeros(1, requires_grad=True)

• 定义线性回归模型、这里
  $${\hat{y}}^{(i)}={x_1}^{(i)}{w}_1+{x_2}^{(i)}{w}_2+b$$
  其中${\hat{y}}^{(i)}$为由第$i$条特征数据与模型参数 w 和 b 运算后求得的拟合值

def LinearRegression(X, w, b):    
    return torch.matmul(X, w) + b     # 对应元素相乘再相加

• 定义损失函数、即均方误差
  $$l^{(i)}(w_1,w_2,b)=\frac{1}{2}{({\hat{y}}^{(i)}-y^{(i)})}^2$$
  其中$y^{(i)}$为第$i$条数据对应的真实值

def squared_loss(y_hat, y):          #  传入拟合值与真实值
    return (y_hat - y) ** 2 / 2      #  返回二维张量

• 定义优化算法、即随机梯度下降Stochastic gradient descent
• 求偏导是对损失函数 squared_loss 中的模型参数 w 和 b 求的偏导、实际上这里只是完成了对参数的更新、并没有使用反向传播
• 注意更新完成后将梯度清零

def sgd(params, lr, batch_size):   # 传入参数列表、学习率以及小批量的大小
    # 小批量随机梯度下降
    with torch.no_grad():          # 更新时解除梯度运算
        for param in params:
            # 学习率与参数梯度的乘积除以批量大小
            param -= lr * param.grad / batch_size
            param.grad.zero_()      # 将梯度清零

• 对线性回归模型进行训练
• 设置迭代的轮次 num_epochs 、在每轮迭代中、不断地从数据迭代器 data_iter 中拿到小批量的数据 X 和 y 来对模型进行训练
• 计算模型在这些小批量上的拟合值 LinearRegression(X, w, b) 与真实值 y 之间的损失 (squared_loss) 、以此得知参数 w 和 b 该如何变化
• 对参数 w 和 b 更新 (sgd) 后再在下一个小批量上重复、所有的数据均参与训练后即完成了一轮迭代

learning_rate = 0.03    # 学习率
num_epochs = 3          # 迭代次数
net = LinearRegression  # 选择模型
loss = squared_loss     # 损失函数

# 对所有数据的迭代进行控制
for epoch in range(num_epochs):     
    # 在所有数据的小批量上不断使损失最小化
    for X, y in data_iter(batch_size, features, label):
        L = loss(net(X, w, b), y)     # 拟合结果在小批量上的损失
        L.sum().backward()            # 对损失求和后计算[w, b]的梯度
        sgd([w, b], learning_rate, batch_size)  # 由梯度对参数进行更新、单纯地传入batch_size是不合适的
        
    # 将迭代轮次与损失打印出来
    with torch.no_grad():
        train_L = loss(net(features, w, b), label)
        print(f'epoch{epoch + 1}, loss{float(train_L.mean()): f}')
        

epoch1, loss 0.028120
epoch2, loss 0.000129
epoch3, loss 0.000050

• 将参数的估计量与真实值进行比较、可以看到真的是非常接近的

print('   actual w: ', true_w, '\nestimated w: ', w)
print('   actual b: ', true_b, '\nestimated b: ', b)

   actual w:  tensor([ 3.0000, -2.4000]) 
estimated w:  tensor([[ 2.9995],
        [-2.3995]], requires_grad=True)
   actual b:  tensor([2.4000]) 
estimated b:  tensor([2.3992], requires_grad=True)

---

---

• 实际上、在上面的过程中、模型参数 w 和 b 的变化过程还不是特别清楚、下面对训练过程做进一步的拆解
• 在优化算法 sgd 中、将更新前的参数 param 、学习率 lr 、参数变量的梯度 param.grad、批量大小 batch_size 以及更新后的参数 param.updated 整理成一个数据框后打印出来
• 注意观察 在这一组小批量上更新后的参数 与 在下一组小批量上更新前的参数 是否相同
• （肯定相同啊）

p = ['_w', '_b']  # 参数名的后缀、打印前做拼接

import pandas as pd

def sgd(params, lr, batch_size):   # 传入参数列表、学习率以及小批量的大小
    
    # 小批量随机梯度下降
    with torch.no_grad():          # 更新时解除梯度运算
        
        for i, param in enumerate(params):
            
            name = 'param' + p[i]
            param_value = param.detach().numpy().reshape(-1)              ##  更新前的参数
            param_grad  = param.grad.detach().numpy().reshape(-1)         ##  参数变量的梯度
            
            print(pd.DataFrame({name: param_value,
                                '- (lr * ': lr,
                                name + '.grad': param_grad,
                                '/ batch_size) = ': batch_size,
                                name + '.updated': param_value - lr * param_grad / batch_size}))
            
            # 学习率与参数梯度的乘积除以批量大小
            param -= lr * param.grad / batch_size
            # 将梯度清零
            param.grad.zero_()     
            

• 这里并不令模型 在所有的数据上反复迭代 训练、只考虑一轮迭代中、模型在每个小批量数据上的训练结果
• 重新生成100条数据、批量大小设置为25、所以模型此时在一轮迭代中会对参数更新100 / 25 即 4次
• 将数据的真实值 y_true 、模型的拟合值 y_hat 以及损失值 loss 整理成数据框后打印出来

# 重新初始化模型参数
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# 减少数据量、只生成100条数据
F, L = synthetic_data(true_w, true_b, num_examples=100)
# 减小批量大小
batch_size = 25

# 在所有数据的小批量上不断使损失最小化
for i, (X, y) in enumerate(data_iter(batch_size, F, L)):
    
    # 打印这是第几个小批量
    print('----------------------------------------------------------------------------------')
    print(('  BATCH  ' + str(i + 1)) * 8)
    print('----------------------------------------------------------------------------------')
    
    y_true = y[: 5].numpy().reshape(-1)                               ## 真实值
    y_hat = net(X, w, b )[: 5].detach().numpy().reshape(-1)           ## 在现在的参数取值下、根据回归模型求所谓的拟合值、只取前5个
    
    L = loss(net(X, w, b), y)                                         # 拟合结果在小批量上的损失
    loss_ = L[: 5].detach().numpy().reshape(-1)                      ## 损失值
    
    print(pd.DataFrame({'y_true:'   : y_true,
                        'y_hat': y_hat,
                        'loss' : loss_,
                        '(y - y_hat) ** 2 / 2': (y_true - y_hat) ** 2 / 2}))
    
    L.sum().backward()            # 相当于计算[w, b]的梯度
    sgd([w, b], learning_rate, batch_size)  # 由梯度对参数进行更新
    # 已经在优化函数sgd（）中增加了想要打印的内容、即参数取值、参数梯度以及更新后的参数

# 本轮迭代后的损失
train_L = loss(net(features, w, b), label)
print('----------------------------------------------------------------------------------')
print(f'LOSS{float(train_L.mean()): f}')

----------------------------------------------------------------------------------
  BATCH  1  BATCH  1  BATCH  1  BATCH  1  BATCH  1  BATCH  1  BATCH  1  BATCH  1
----------------------------------------------------------------------------------
    y_true:     y_hat       loss  (y - y_hat) ** 2 / 2
0 -0.131016 -0.014049   0.006841              0.006841
1  5.906297  0.015085  17.353189             17.353189
2  0.881901  0.003036   0.386202              0.386202
3 -0.001573 -0.011868   0.000053              0.000053
4  7.636694  0.016791  29.031466             29.031466
    param_w  - (lr *   param_w.grad  / batch_size) =   param_w.updated
0  0.005106      0.03    -44.389107                25         0.058373
1 -0.010283      0.03     82.359451                25        -0.109114
   param_b  - (lr *   param_b.grad  / batch_size) =   param_b.updated
0      0.0      0.03    -48.316177                25         0.057979
----------------------------------------------------------------------------------
  BATCH  2  BATCH  2  BATCH  2  BATCH  2  BATCH  2  BATCH  2  BATCH  2  BATCH  2
----------------------------------------------------------------------------------
    y_true:     y_hat       loss  (y - y_hat) ** 2 / 2
0 -0.443789 -0.007321   0.095252              0.095252
1 -0.984652 -0.062500   0.425182              0.425182
2  7.227615  0.215972  24.581572             24.581572
3  0.624471  0.041280   0.170056              0.170056
4 -3.099711 -0.153484   4.340127              4.340127
    param_w  - (lr *   param_w.grad  / batch_size) =   param_w.updated
0  0.058373      0.03    -43.017033                25         0.109993
1 -0.109114      0.03     56.293491                25        -0.176666
    param_b  - (lr *   param_b.grad  / batch_size) =   param_b.updated
0  0.057979      0.03    -36.868214                25         0.102221
----------------------------------------------------------------------------------
  BATCH  3  BATCH  3  BATCH  3  BATCH  3  BATCH  3  BATCH  3  BATCH  3  BATCH  3
----------------------------------------------------------------------------------
    y_true:     y_hat       loss  (y - y_hat) ** 2 / 2
0 -1.189351 -0.184881   0.504480              0.504480
1  7.701901  0.345547  27.057970             27.057970
2 -1.287672 -0.124485   0.676502              0.676502
3 -0.284723 -0.038631   0.030281              0.030281
4 -3.866466 -0.106044   7.070389              7.070389
    param_w  - (lr *   param_w.grad  / batch_size) =   param_w.updated
0  0.109993      0.03   -108.227051                25         0.239866
1 -0.176666      0.03     39.138115                25        -0.223632
    param_b  - (lr *   param_b.grad  / batch_size) =   param_b.updated
0  0.102221      0.03    -43.831829                25         0.154819
----------------------------------------------------------------------------------
  BATCH  4  BATCH  4  BATCH  4  BATCH  4  BATCH  4  BATCH  4  BATCH  4  BATCH  4
----------------------------------------------------------------------------------
    y_true:     y_hat       loss  (y - y_hat) ** 2 / 2
0  6.129820  0.446178  16.151894             16.151894
1  0.280920 -0.017562   0.044546              0.044546
2 -0.783369 -0.131024   0.212777              0.212777
3  2.809025  0.212253   3.371614              3.371614
4  7.629917  0.592282  24.764153             24.764153
    param_w  - (lr *   param_w.grad  / batch_size) =   param_w.updated
0  0.239866      0.03    -96.464478                25         0.355623
1 -0.223632      0.03     78.339828                25        -0.317640
    param_b  - (lr *   param_b.grad  / batch_size) =   param_b.updated
0  0.154819      0.03    -39.180454                25         0.201836
----------------------------------------------------------------------------------
LOSS 7.742309

• 仔细观察是可以更清楚地明白整个参数的更新过程是如何进行的
• 打印出来的损失值 LOSS 似乎不太合理、这一方面是因为数据量 num__examples 从原来的1000减少到100、另一方面是因为设置的批量 batch_size 相对于数据量本身来说是很大的、所以此时的损失仍然较大
• 不妨同样将数据量 num__examples 设置为1000、批量大小 batch_size 设置为10再试试看？

---

---

• 最后从公式上再来看看 这该死的梯度到底怎么求的？
• 或者说对模型参数$w_1$的更新是如何完成的？
• 这是模型在小批量$\mathcal{B}$上、真实值与拟合值之间的平均损失
  $$\frac{1}{\left|\mathcal{B}\right|}\sum _{i\in |\mathcal{B}|}\frac{1}{2}{(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)})}^2$$
• 对上面的平均损失函数关于模型参数$w_1$求导后即得到所谓的 梯度 、即
  $$\frac{1}{\left|\mathcal{B}\right|}\sum _{i\in |\mathcal{B}|}{x}_1^{(i)}(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)})$$
• 实际上对
  $$\frac{1}{2}{(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)})}^2$$
  关于参数$w_1$求导后可以得到
  $$x_1^{(i)}(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)})$$
• 最后让原来的参数$w_1$减去梯度与学习率$\eta$乘积，即
  $$w_1-\frac{\eta }{\left|\mathcal{B}\right|}\sum _{i\in |\mathcal{B}|}{x}_1^{(i)}(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)})$$
  来完成参数$w_1$的更新