反向传播算法 Python实现
反向传播算法 Python实现
- 1. BP算法简述
- 2. 参数初始化
- 3. 激活函数及其导数
- 4. 损失函数
- 5. 前向传播
- 6. 反向传播
1. BP算法简述
反向传播算法,简称BP算法,适合于多层神经元网络的一种学习算法,它建立在梯度下降法的基础上。BP网络的输入输出关系实质上是一种映射关系:一个n输入m输出的BP神经网络所完成的功能是从n维欧氏空间向m维欧氏空间中一有限域的连续映射,这一映射具有高度非线性。它的信息处理能力来源于简单非线性函数的多次复合,因此具有很强的函数复现能力。这是BP算法得以应用的基础。
2. 参数初始化
这里使用np.random.normal函数随机初始化。modelconfig表示模型配置,包括输入层和输出层,注意输入层和输出层需要和数据维度相对应;bias表示是否设置偏置项,这里将参数w和偏置b放在一起考虑。
def parameter_initializer(modelconfig = [3, 16, 3], bias = True): # n1, n2, n3
""" 初始化权值 """
W = []
for i in range(len(modelconfig)-2):
if bias:
w = np.random.normal(scale=(2.0/modelconfig[i])**0.5, size=(modelconfig[i] + 1, modelconfig[i+1]+1))
else:
w = np.random.normal(scale=(2.0/modelconfig[i])**0.5, size=(modelconfig[i], modelconfig[i+1]))
W.append(w)
if bias:
w = np.random.normal(scale=(2.0/modelconfig[i])**0.5, size=(modelconfig[-2] + 1, modelconfig[-1]))
else:
w = np.random.normal(scale=(2.0/modelconfig[i])**0.5, size=(modelconfig[-2], modelconfig[-1]))
W.append(w)
return W
3. 激活函数及其导数
这里应用sigmoid作为输出层的激活函数,tanh作为隐藏层的激活函数。sigmoid_deriv和tanh_deriv分别是sigmoid和tanh的导数。
def sigmoid(z):
a = 1/(1+np.exp(-z))
return a
def sigmoid_deriv(x):
# sigmoid的导数
return x * (1 - x)
def tanh(z):
a = np.tanh(z)
return a
def tanh_deriv(z):
z = 1 - z ** 2
return z
4. 损失函数
这里使用平方误差准则函数作为损失(目标)函数。
def loss(output, y):
""" 损失函数 """
#print(output.shape, y.shape)
#cross_entropy = -((1-y)*np.log(1-output) + y * np.log(output)) 可以尝试交叉熵
#cost = np.mean(np.sum(cross_entropy, axis=1))
Loss = (output - y) ** 2
cost = np.mean(np.sum(Loss, axis=1))
return cost
5. 前向传播
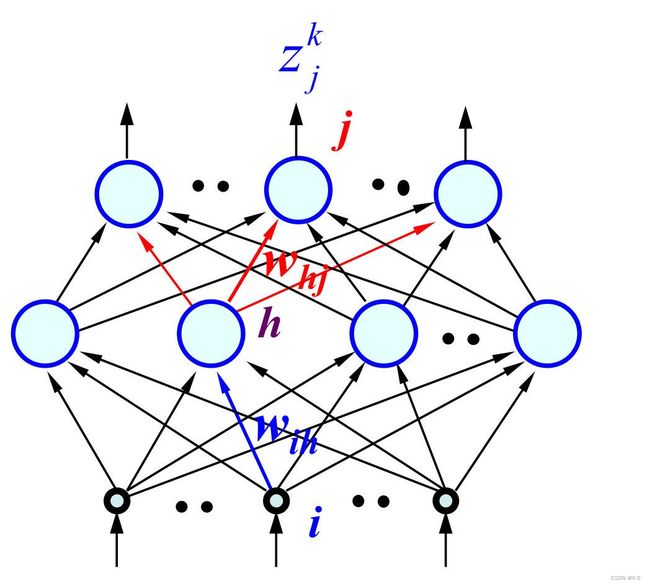
下面代码是前向传播函数。隐藏层激活函数默认使用tanh,输出层使用Sigmoid。三层模型的前向传播计算公式如下:
y h k = f ( n e t h k ) = f ( ∑ i w i h x i k ) y_h^k = f(net_h^k) = f(\sum_{i}w_{ih}x_i^k) yhk=f(nethk)=f(∑iwihxik)
z j k = f ( n e t j k ) = f ( ∑ h w h j y h k ) z_j^k = f(net_j^k) = f(\sum_{h}w_{hj}y_h^k) zjk=f(netjk)=f(∑hwhjyhk)
其中 i i i表示输入大小, h h h表示隐藏层尺寸, j j j表示输出尺寸, k k k表示样本编号。
def forward_propagate(x, W):
""" 前向传播 """
A = []
z = copy.deepcopy(x)
for i in range(len(W)-1): # 输入到隐藏层
z = np.dot(z, W[i])
z = tanh(z)
A.append(z)
i += 1
z = np.dot(z, W[i])
z = sigmoid(z) # 隐藏层到输出,使用sigmoid函数
A.append(z)
return A
6. 反向传播
反向传播计算相对更复杂。这里首先基于平方误差准则函数得到的损失值,计算一个样本 k k k对输入层到隐藏层参数 w i h k w_{ih}^k wihk、隐藏层到输出层参数 w h j w_{hj} whj的梯度,公式如下:
Δ w h j = − η ∂ E ∂ w h j \Delta w_{hj}= - \eta \frac{\partial E}{ \partial w_{hj}} Δwhj=−η∂whj∂E
= − η ∑ k ∂ E ∂ y j k ∂ y j k ∂ n e t j k ∂ n e t j k ∂ w h j =- \eta \sum_{k} \frac{\partial E}{\partial y_j^k} \frac{\partial y_j^k}{\partial net_j^k}\frac{\partial net_j^k}{\partial w_{hj}} =−η∑k∂yjk∂E∂netjk∂yjk∂whj∂netjk
= η ∑ k ( t j k − z j k ) f ′ ( n e t j k ) y h k = \eta \sum_{k}(t_j^k - z_j^k)f'(net_j^k)y_h^k =η∑k(tjk−zjk)f′(netjk)yhk
= η ∑ k ( t j k − z j k ) z j k ( 1 − z j k ) y h k = \eta \sum_{k} (t_j^k-z_j^k)z_j^k(1-z_j^k)y_h^k =η∑k(tjk−zjk)zjk(1−zjk)yhk
Δ w i h = − η ∂ E ∂ w i h \Delta w_{ih}= - \eta \frac{\partial E}{ \partial w_{ih}} Δwih=−η∂wih∂E
= − η ∑ k ∂ E ∂ y j k ∂ y j k ∂ n e t j k ∂ n e t j k ∂ z h k ∂ z h k ∂ n e t h k ∂ n e t h k ∂ w i h =- \eta \sum_{k} \frac{\partial E}{\partial y_j^k} \frac{\partial y_j^k}{\partial net_j^k}\frac{\partial net_j^k}{\partial z_h^k} \frac{\partial z_h^k}{\partial net_h^k} \frac{\partial net_h^k}{\partial w_{ih}} =−η∑k∂yjk∂E∂netjk∂yjk∂zhk∂netjk∂nethk∂zhk∂wih∂nethk
= η ∑ k ( t j k − z j k ) z j k ( 1 − z j k ) w h j y h k ( 1 − y h k ) x i k = \eta \sum_{k} (t_j^k-z_j^k)z_j^k(1-z_j^k)w_{hj}y_h^k(1-y_h^k)x_i^k =η∑k(tjk−zjk)zjk(1−zjk)whjyhk(1−yhk)xik
def back_propagate(x, W, A, label, config):
A.insert(0, x)
m = y.shape[0]
D = [(A[-1] - label) * sigmoid_deriv(A[-1])]
n = 0
for layer in range(len(A)-2, 0, -1):
delta = D[-1].dot(W[layer].T)
delta = delta * tanh_deriv(A[layer])
D.append(delta)
D = D[::-1]
for layer in range(0, len(W)):
W[layer] += - config['learning_rate'] * A[layer].T.dot(D[layer])
return W
完整代码:
from sklearn.model_selection import train_test_split
import numpy as np
import copy
np.random.seed(123) # 需要固定种子,不然初始化参数会变动,训练结果也会变动
def parameter_initializer(modelconfig = [3, 16, 16, 3], bias = True): # n1, n2, n3
""" 初始化权值 """
W = []
for i in range(len(modelconfig)-2):
if bias:
w = np.random.normal(scale=(2.0/modelconfig[i])**0.5, size=(modelconfig[i] + 1, modelconfig[i+1]+1))
else:
w = np.random.normal(scale=(2.0/modelconfig[i])**0.5, size=(modelconfig[i], modelconfig[i+1]))
W.append(w)
if bias:
w = np.random.normal(scale=(2.0/modelconfig[i])**0.5, size=(modelconfig[-2] + 1, modelconfig[-1]))
else:
w = np.random.normal(scale=(2.0/modelconfig[i])**0.5, size=(modelconfig[-2], modelconfig[-1]))
W.append(w)
return W
def sigmoid(z):
a = 1/(1+np.exp(-z))
return a
def sigmoid_deriv(x):
# sigmoid的导数
return x * (1 - x)
def tanh(z):
a = np.tanh(z)
return a
def tanh_deriv(z):
z = 1 - z ** 2
return z
def forward_propagate(x, W):
""" 前向传播 """
A = []
z = copy.deepcopy(x)
for i in range(len(W)-1):
z = np.dot(z, W[i])
z = tanh(z)
A.append(z)
i += 1
z = np.dot(z, W[i])
z = sigmoid(z)
A.append(z)
return A
def loss(output, y):
""" 损失函数 """
#print(output.shape, y.shape)
#cross_entropy = -((1-y)*np.log(1-output) + y * np.log(output)) 可以尝试交叉熵
Loss = (output - y) ** 2
cost = np.mean(np.sum(Loss, axis=1))
return cost
def back_propagate(x, W, A, label, config):
A.insert(0, x)
m = y.shape[0]
D = [(A[-1] - label) * sigmoid_deriv(A[-1])]
n = 0
for layer in range(len(A)-2, 0, -1):
delta = D[-1].dot(W[layer].T)
delta = delta * tanh_deriv(A[layer])
D.append(delta)
D = D[::-1]
for layer in range(0, len(W)):
W[layer] += - config['learning_rate'] * A[layer].T.dot(D[layer])
return W
def bpnn_batch(x, y, config):
# 模型参数初始化
W = parameter_initializer(modelconfig = config['model_config'], bias = config['bias'])
for epoch in range(config['epochs']):
# 批量处理
A = forward_propagate(x, W)
cost = loss(A[-1], y)
W = back_propagate(x, W, A, y, config)
y_pred = np.argmax(A[-1],axis=1)
y_true = np.argmax(y, axis=1)
print("{} epoch, cost is {}".format(epoch, cost), sum(list(y_pred==y_true))/y.shape[0])
return W
def bpnn_single(x, y, config):
# 模型参数初始化
W = parameter_initializer(modelconfig = config['model_config'], bias = config['bias'])
for epoch in range(config['epochs']):
# 单样本处理
cost = 0
y_pred = np.empty((1,))
y_true = np.empty((1,))
for i in range(x.shape[0]):
A = forward_propagate(np.expand_dims(x[i], axis=0), W)
cost += loss(A[-1], np.expand_dims(y[i], axis=0))
W = back_propagate(np.expand_dims(x[i], axis=0), W, A, np.expand_dims(y[i], axis=0), config)
y_pred = np.append(y_pred, np.argmax(A[-1],axis=1), axis=0)
y_true = np.append(y_true, np.argmax(np.expand_dims(y[i], axis=0), axis=1), axis=0)
print("{} epoch, cost is {}".format(epoch, cost), sum(list(y_pred[1:]==y_true[1:]))/y.shape[0])
return W
if __name__ == "__main__":
# Configuration
config = {"bias":False, "learning_rate":0.1, "model_config":[3, 16, 16, 3],
"epochs":200, "test_size":0.2, "batch":False}
# 加载数据集
x1 = [[1.58, 2.32, -5.8], [ 0.67, 1.58, -4.78], [ 1.04, 1.01, -3.63],
[-1.49, 2.18, -3.39], [-0.41, 1.21, -4.73], [1.39, 3.16, 2.87],
[ 1.20, 1.40, -1.89], [-0.92, 1.44, -3.22], [ 0.45, 1.33, -4.38],
[-0.76, 0.84, -1.96]]
x2 = [[ 0.21, 0.03, -2.21], [ 0.37, 0.28, -1.8], [ 0.18, 1.22, 0.16],
[-0.24, 0.93, -1.01], [-1.18, 0.39, -0.39], [0.74, 0.96, -1.16],
[-0.38, 1.94, -0.48], [0.02, 0.72, -0.17], [ 0.44, 1.31, -0.14],
[ 0.46, 1.49, 0.68]]
x3 = [[-1.54, 1.17, 0.64], [5.41, 3.45, -1.33], [ 1.55, 0.99, 2.69],
[1.86, 3.19, 1.51], [1.68, 1.79, -0.87], [3.51, -0.22, -1.39],
[1.40, -0.44, -0.92], [0.44, 0.83, 1.97], [ 0.25, 0.68, -0.99],
[ 0.66, -0.45, 0.08]]
x = np.vstack((np.array(x1), np.array(x2), np.array(x3)))
y=[0]*len(x1) + [1]*len(x2) + [2]*len(x3)
y = np.eye(3)[y]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=config["test_size"], random_state=66)
if config['bias']:
x_train = np.c_[x_train, np.ones((x_train.shape[0]))]
if config["batch"]:
W = bpnn_batch(x_train, y_train, config)
else:
W = bpnn_single(x_train, y_train, config)
print(W)
# 测试效果
if config['bias']:
x_test = np.c_[x_test, np.ones((x_test.shape[0]))]
A = forward_propagate(x_test, W)
cost = loss(A[-1], y_test)
y_pred = np.argmax(A[-1],axis=1)
y_true = np.argmax(y_test, axis=1)
print("Cost:", cost, "Accuracy:", sum(list(y_pred==y_true))/y_test.shape[0])
反制CSDN中需要登陆才能复制的规定,开源完整代码文件:Jupyter notebook | .py文件