纯Python实现反向传播(BP算法)(5)
目录
- 1.反向传播求偏导(买两个苹果+税:求导)
- 2.加了加法层的BP算法)
- 3.Softmax+Cross entrop error反向传播)
- 4.总结
看鱼书记录5:
数值微分和反向传播都能更新权值的梯度度(严格来说,是损失函数关于权重参数的梯度),但反向传播更加高效。
反向传播就是求偏导(梯度),如何求呢?根据链式法则和输入值来求,具体如下

该点的局部导数是对上一个结点的偏导(从右到左(上一个结点))
- 加法节点的反向传播将上游的值原封不动地输出到下游(因为对上一个结点求偏导为1,这里的值是指上一个对下一个传递的偏导值)
- 乘法结点的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。
- 加法的反向传播只是将上游的值传给下游,并不需要正向传播的输入信号。但是,乘法的反向传播需要正向传播时的输入信号值。因此,实现乘法节点的反向传播时,要保存正向传播的输入信号。
看懂下面这个例子就知道加法、乘法这个偏导怎么从右边传递到左边了: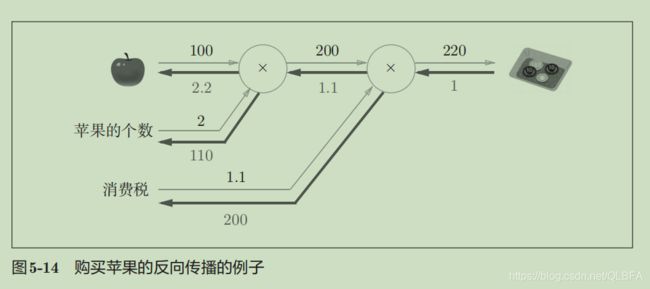
箭头下面代表偏导,如2.2代表如何苹果价格(上图苹果100代表它的价格)上升,将对最终总消费额产生2.2倍大小的影响。下面通过代码实现5-14(反向传播求偏导)
1.反向传播求偏导(买两个苹果+税:求导)
import numpy as np
import matplotlib.pyplot as plt
class Mullayer:
def __init__(self):
self.x=None
self.y=None
#前向传播
def forward(self,x,y):
self.x=x
self.y=y
out=x*y
return out
#反向传播,dout是上一个传给下一个结点的偏导数
def backward(self,dout):
#这里乘法层,所有翻转了
dx=dout*self.y
dy=dout*self.x
return dx,dy
apple=100
apple_num=2
tax=1.1
#代表两个结点(对象),要用两个对象哦,不然结果出错(因为输入了不同的输入值)
mul_apple_layer=Mullayer()
mul_tax_layer=Mullayer()
#进行前向传播
apple_price=mul_apple_layer.forward(apple,apple_num)
price=mul_tax_layer.forward(apple_price,tax)
print(price)
#下面进行反向传播求导数
dprice=1
dapple_price,dtax=mul_tax_layer.backward(dprice)
print(dapple_price,dtax)
dapple,dapple_num=mul_apple_layer.backward(dapple_price)
print(dapple,dapple_num)
输出:
220.00000000000003
1.1 200
2.2 110.00000000000001
与图5-14的结果一样
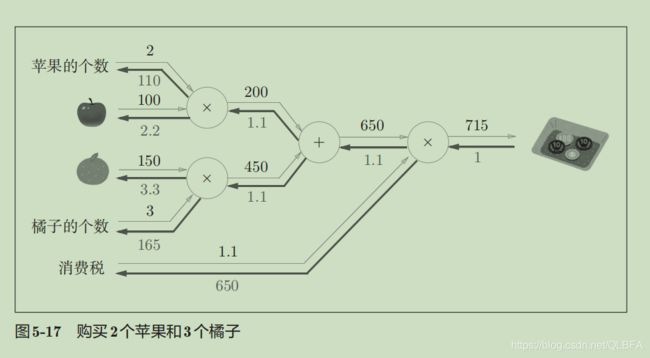
2.加了加法层的BP算法
import numpy as np
import matplotlib.pyplot as plt
#加法结点层
class AddLayer:
def __init__(self):
pass
def forward(self,x,y):
out=x+y
return out
def backward(self,dout):
dx=dout*1
dy=dout*1
return dx,dy
#乘法结点层
class Mullayer:
def __init__(self):
self.x=None
self.y=None
#前向传播
def forward(self,x,y):
self.x=x
self.y=y
out=x*y
return out
#反向传播,dout是上一个传给下一个结点的偏导数
def backward(self,dout):
#这里乘法层,所有翻转了
dx=dout*self.y
dy=dout*self.x
return dx,dy
apple=100
apple_num=2
orange=150
orange_num=3
tax=1.1
#结点对象
mul_apple_layer=Mullayer()
mul_orange_layer=Mullayer()
add_apple_orange_layer=AddLayer()
mul_tax_layer=Mullayer()
#前向传播
apple_price=mul_apple_layer.forward(apple,apple_num)
orange_price=mul_orange_layer.forward(orange,orange_num)
all_price=add_apple_orange_layer.forward(apple_price,orange_price)
price=mul_tax_layer.forward(all_price,tax) #最终价格
#反向传播求偏导
dprice=1
dall_price,dtax=mul_tax_layer.backward(dprice)
dapple_price,dorange_price=add_apple_orange_layer.backward(dall_price)
dorange,dorange_num=mul_orange_layer.backward(dorange_price)
dapple,dapple_num=mul_apple_layer.backward(dapple_price)
print(price)
print(dapple,dorange,dorange_num,dapple_num,dtax)
输出:
715.0000000000001
2.2 3.3000000000000003 165.0 110.00000000000001 650
输出的结果和上图一样,内容和1基本一样,只不过+了加法层
仿射变换:包括一次线性变换和一次平移,分别对应神经网络的加权和运算与加偏置运算。eg:wx+b
3.Softmax+Cross entrop error反向传播
import numpy as np
def softmax(a):
exp_a=np.exp(a)
sum_exp_a=np.sum(exp_a)
y=exp_a/sum_exp_a
return y
#t代表真实训练数据
def cross_entropy_error(y,t):
#y是一维的情况
if y.ndim==1:
#转为二维:shape是(1,t.size)的类型(这里是1,10),而不是一维shape(t.size,)的情况(这里是10,)了
t=t.reshape(1,t.size)
y=y.reshape(1,y.size)
batch_size=y.shape[0] #1
return -np.sum(t*np.log(y+1e-7))/batch_size #就是又多少行(batch_size),就除以多少,这就是小批量来估计整体
class SoftmaxwithLoss:
def __init__(self):
self.loss=None
self.y=None
self.t=None
def forward(self,x,t):
self.t=t
self.y=softmax(x)
self.loss=cross_entropy_error(self.y,self.t)
return self.loss
def backwarrd(self,dout=1):
batch_size=self.t.shape[0]
dx=(self.y-self.t)/batch_size
return dx
a=SoftmaxwithLoss()
x=np.array([3,1,6]) #预测结果
t=np.array([0,1,0]) #真实数据(训练数据)
print(a.forward(x,t))
print(a.backwarrd())
输出:
5.054969555278561
[ 0.01570781 -0.33120751 0.31549971]
这里由于预测跟真实相差比较大,所有最终loss(前向传播)也比较大;而由于误差大,所有反向传播的结果返回的也比较大:-0.33,因为这个大的误差会向前面的层传播,所以Softmax层前面的层会从这个大的误差中学习到“大”的内容。
4.总结
步骤1(mini-batch)
从训练数据中随机选择一部分数据。
步骤2(计算梯度)
计算损失函数关于各个权重参数的梯度。
步骤3(更新参数)
将权重参数沿梯度方向进行微小的更新。
步骤4(重复)
重复步骤1、步骤2、步骤3。