一些名词解释——band-pass filter；high-pass filter； L1/L2 norm；欧几里得距离；特征向量

最近在读文献，遇到了一些新接触的专业名词，在此记录下来。

有：L1 L2 norm, band-pass/high-pass filter (带通、高通滤波)，欧几里得距离、特征向量（Feature Vector）

L1 L2 norm

p范数表示为 $L_p$,其中，$p=0,1,2,3$。$L_p$的表达式为：
$$L_p=(|x_1{|}^p+|x_2{|}^p+\cdots +|x_n{|}^p{)}^{1/p}$$

当 p=0 时，$L_0$ 指的是向量中非 0 元素的个数
当 p=1 时，$L_1$ 指的是向量中各个元素的绝对值之和
当 p=2 时，$L_2$ 指的是向量 $(x_1,x_2,\cdots ,x_n)$ 的模长

参考博客：这个

滤波相关

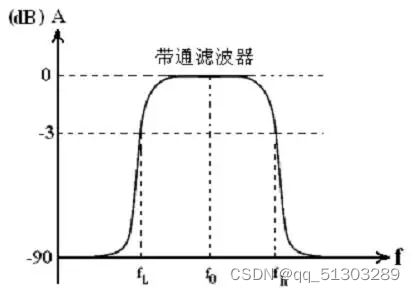
带通滤波器 (band-pass filter)

带通滤波器是指能通过某一频率范围内的频率分量、但将其他范围的频率分量衰减到极低水平的滤波器，与带阻滤波器的概念相对。一个模拟带通滤波器的例子是电阻-电感-电容电路(RLC circuit)。这些滤波器也可以用低通滤波器同高通滤波器组合来产生.(来源某百科)

下图为带通滤波器，纵坐标为振幅（强度），横坐标为频率。

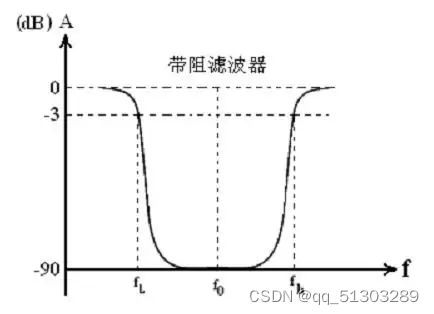
相应地，也有带阻滤波器(band-stop filter)：

高通滤波器(high-pass filter)

高通滤波器，又称低截止滤波器、低阻滤波器，允许高于某一截频的频率通过，而大大衰减较低频率的一种滤波器 。它去掉了信号中不必要的低频成分或者说去掉了低频干扰。(来源某百科)

同理，也有低通滤波器(高阻滤波器)。

几种滤波器的滤波效果图如下：

• LPF : Low-Pass Filter
• HPF: High-Pass Filter
• BPF: Band-Pass Filter
• BRF: Band-Resist Filter

欧几里得距离

在数学中，欧几里得距离或欧几里得度量是欧几里得空间中两点间“普通”（即直线）距离。使用这个距离，欧氏空间成为度量空间。相关联的范数称为欧几里得范数。较早的文献称之为毕达哥拉斯度量。

表达式为：
$$|x|=\sqrt{|x{|}_1^2+|x{|}_2^2+\cdots +|x{|}_n^2}$$

（其实就是 $L_2$ 范数）

参考资料：这个

特征向量 (feature vector)

我有一本黑皮书在这个人手上，然后我让她帮我查有没有这个名词的解释，结果她没查到。于是我只好网上冲浪了好一会儿，才终于理解了特征向量这玩意。 期间甚至还以为和线代里面的特征向量是一回事，太丢人了呜呜呜呜呜呜呜~

我们定义一个 n 维向量，用于描述一个对象的 n 个特征。设这个向量为 $a$,那么有 m 个对象，分别用 $a_1,a_2,\cdots ,a_m$ 进行描述，那么 $\{a_1,a_2,\cdots ,a_m\}$ 则称为这些数据的 特征向量(feature vector)。

举个例子，我们取 n=3 ，即描述三个特征，假设分别为是否为球形、是否有花纹、是否是运动器材

对于篮球、羽毛球、斯诺克台球、麻球（一种食物），它们的特征向量分别为：

$$a_{篮球}=\{1,1,1\}$$

$$a_{羽毛球}=\{0,1,1\}$$

$$a_{台球}=\{1,0,1\}$$

$$a_{麻球}=\{1,0,0\}$$

之所以叫特征向量，显而易见，因为这个是描述训练数据集特征的矢量。