Manacher 算法：最大回文字符串

尝试理解Manacher算法…

《647. 回文子串》
《剑指 Offer II 020. 回文子字符串的个数》
《5. 最长回文子串》

【判断一个字符串是不是回文？】
字符串反转；
字符串反转一半；
双指针原地判断；

【一个字符串s有几个回文子字符串？】

方法一：暴力先试一下

遍历字符串s的所有子字符串，判断是不是回文；

时间复杂度 $O(n^2)$；
空间复杂度$O(1)$；

class Solution:
    def countSubstrings(self, s: str) -> int:
    	# 判断字符串st从i到j是不是回文
        def check(st,i,j):
            while i <= j:
                if st[i] != st[j]:
                    return False
                else:
                    i += 1
                    j -= 1
            return True

        
        n = len(s)
        res = 0
        # 遍历所有字串
        for i in range(n):
            for j in range(i,n):
                flag = check(s,i,j)
                if flag:
                    res += 1
        return res

方法二：中心扩展

暴力法的问题在于，重复解子问题；

举个栗子：s = “acbca”
判定"cbc"时需要重复判定"b"，其实"b"是回文只要判定"b"两边的"c"是不是；
判定"acbca"时需要重复判定"b"和"cbc"，其实"cbc"是回文只需要判定"cbc"两边的"a"是不是；

…是这么个道理吧

这世界上还有一个道理那就是，回文串的性质就是：对称对称对称!

那就从中心点开始找吧：

case1

当前指针i指向s[0]，当前子字符串长度为1，中心点在s[0]：

对称的两边在哪里？ left = i // 2 = 0
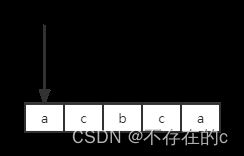
right = (i + 1)//2 = 0

左右还是0啊， 现在只需要判断s[left] == s[right]就ok了；

s[l]和s[r]都是"a"，所以"a"是回文子字符串，res += 1；

case2

当前指针i指向s[1]，当前子字符串长度为2，中心点为0.5，在"a","c"中间：

left = i // 2 = 0
right = (i + 1)//2 = 1
s[left] != s[right]，好了，结束；

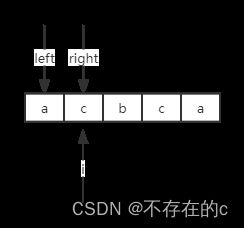
case3

当前指针i指向s[4]，当前子字符串长度为5(子串"acbca")，中心点在s[2] (字符"b")：

这时候的left和right分别在哪？

left = i // 2 = 2
right = (i + 1)//2 = 2

s[left] == s[right] 所以"b"是回文字串，res += 1；

但是，还没完
我们现在的范围是"acbca"，
此时，向下扩展，左指针向左移，右指针向右移；

left -= 1；right += 1；
s[left] = 'c'；s[right] = 'c'；
s[left] == s[right]

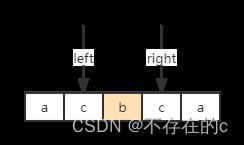
又一个回文子字符串"cbc"， res += 1；


还还没有结束
此时，向下扩展，左指针向左移，右指针向右移；

left -= 1；right += 1；
s[left] = 'a'；s[right] = 'a'；

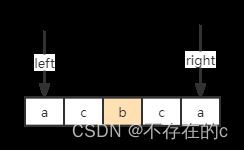
s[left] == s[right]
又一个回文子字符串"acbca"， res += 1；
好了，到边界了，可以结束了;

再说一点点，i遍历到s[4]就可以结束了么？
不行啊，这时候"b"才是中心点（参考上图），后面的"c"，"a"也想当中心点；
此时遍历的范围是2*(len(s))-1，假想后面有一堆空的，"c"和"a"就可以当中心点了；

代码:

class Solution:
    def countSubstrings(self, s: str) -> int:
        # 对暴力优化一下
        res = 0
        n = len(s)

        # 2*n-1 那s[n]就可以是中心点了
        for m in range(2*n-1):
            l = m//2
            r = (m+1)//2
            while l >= 0 and r

方法三：Manacher算法

Manacher 算法是在线性时间内求解最长回文子串的专门算法；

在方法二中心扩展的基础上进行优化；

问题1

方法二存在奇数和偶数不同的情况；
解决：把字符串s填充一下，保证填充后的字符串长度肯定是奇数；

填充规则：

• 在每个字符前后加入一个’#'（分隔符）；
• 并且在头尾加入没出现过的不同的符号（边界）；
• 得到填充后的字符串t；

举个例子：

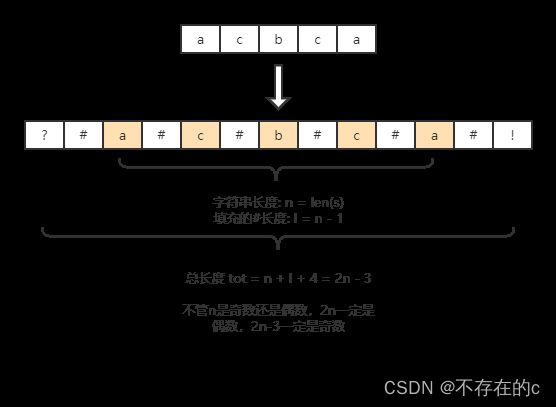
这时候保存填充后的字符串t长度一定是奇数；

问题2

在方法二时，在遍历到中心点mid之前，就知道以m为中心点的回文串的长度；

…那就，浅浅的找个地方存起来吧（以空间换时间，典型DP）

dp[]：记录回文半径，i位置对应的最大的回文串的半径，包含t[i]本身；

n = len(t)
dp = [0] * n

假设已经知道了每个位置i对应的最大回文半径（如上图）：
以t[2]为中心的最大回文为"#a#“，半径为2（“a#”），dp[2] = 2；
以t[3]为中心的最大回文为”#“，半径为1(”#“本身)，dp[3] = 1；
以t[6]为中心的最大回文为”#a#c#b#c#a#"，半径为6(“b#c#a#”)，dp[6] = 6；

然后我们惊奇的发现…
dp[i] // 2 就是当前位置的回文数量;
比如dp[2] = 2，即以t[2]为中心的回文有2 // 2 = 1个，即"a"本身；
比如dp[6] = 6，即以t[5]为中心的回文有6 // 2 = 3个，即"b"，“cbc”，“acbca”；
其余类似，累加即可；

问题来了，dp怎么算？

case1

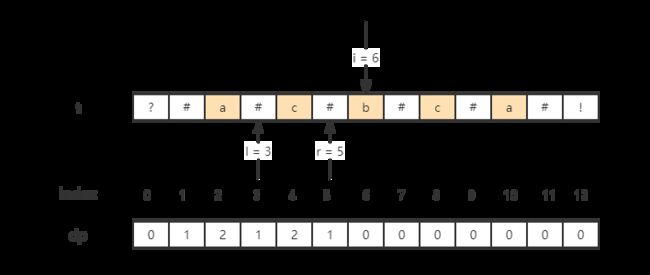
当i = 6时，最近的 + 最长的回文子字符串为"#c#"，即l = 3， r = 5；
i在此范围之外，此时我们对以i为中心的回文子字符串的位置信息一无所知，那么就令dp[i] = 1即可(自己本身)，接下来通过左右同时移动搜索即可，如下:

# i + dp[i]和i - dp[i]刚好关于i对称
while t[i + dp[i]] == t[i - dp[i]]:
		dp[i] += 1         

case2

当i = 8时，最近的最长的回文子字符串为"#a#c#b#c#a#"，即l = 1， r = 11；

i 在此范围之内，i 的回文半径至少为 ：min(dp[i在回文串左边对应点], i到回文串边界的距离 )

说人话，i在这个最大的回文子字符串中，那t[i]肯定是回文子串的一部分嘛…

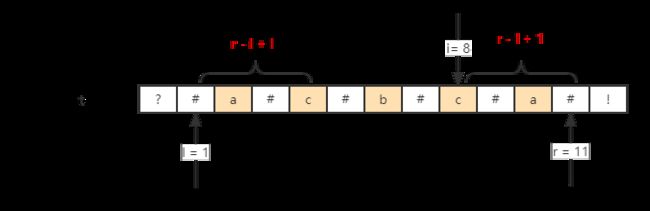
i 离右边边界：r - i + 1 = 4，那起码以4为半径，以t[i]为中心可能是回文字符串；

i 在左边的对应点：r - i + l = 4，dp[4] = 1，那起码以1为半径以t[i]为中心可能是回文字符串；
那是它们两个谁？取两个的最小值；

dp[i] = min(dp[r - i + l], r - i + 1)

不够直观，再来一次
当i = 5时，最近的最长的回文子字符串为"#c#"，即l = 3， r = 5；
i 在此范围之内，i 的回文半径至少为 ：
min(dp[3], 1) = min(1,1) = 1

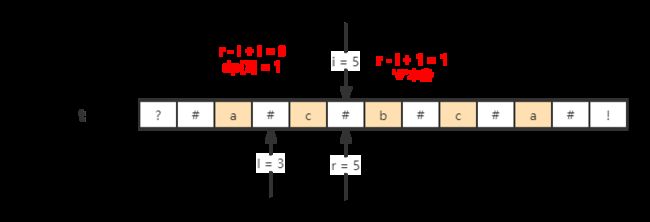
最后的最后，记得更新dp的同时也要更新 l 和 r ：
如果以 i 为中心的回文串比原来更加靠右，则更新 l 和 r ；

全部代码：

class Solution:
    def countSubstrings(self, s: str) -> int:
        # 先填充字符串
        t = "?#"
        for c in s:
            t += c
            t += "#"
        t += "!"
        n = len(t)
        # 填充完毕

        # init
        res = 0
        l,r = 0,0
        dp = [0] * n

        # 遍历字符串t
        # 首尾的边界不用遍历
        for i in range(1,n-1):
            if i > r:
                dp[i] = 1
            else:
                dp[i] = min(r - i + 1,dp[r - i + l])
            
            while t[i + dp[i]] == t[i - dp[i]]:
                dp[i] += 1
            
            if i + dp[i] - 1 > r:
                l = i + 1 - dp[i]
                r = i + dp[i] - 1

            res += (dp[i]//2)
        return res

好了，理解完了。