【机器学习sklearn】决策树（Decision Tree）算法

提示：这里是一只努力肯的小白 有错就改 非礼勿喷:)

---

前言

天可补，海可填，南山可移，日月既往，不可复追。

决策树（Decision Tree）是基于树结构来进行决策的。（分类、回归）
一棵决策树包含一个根结点、若干个内部节点和若干个叶结点。
最终目的是将样本越分越纯。
“伯乐相马” 好典故！！！（摘自决策树分类算法（if-else原理））

---

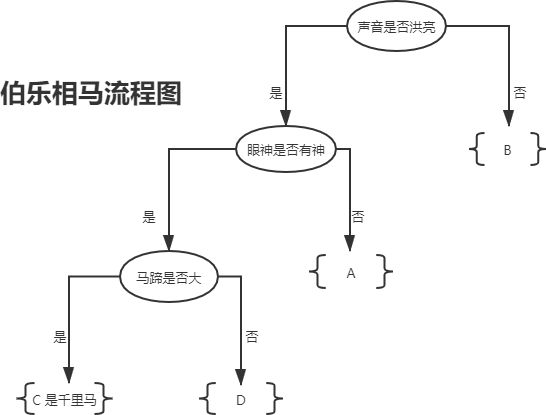
tips: 路漫漫其修远兮 吾将上下而求索

一、决策树学习基本算法

决策树学习的目的是为了产生一棵泛化能力强，即处理未见示例能力强的决策树，遵循“分而治之”（divide-and-conquer）策略。其生成是一个递归的过程。下图为机器学习中的决策树学习基本算法流程（请认真体会~）。

1.信息熵（Information Entropy）

决策树学习的关键是如何选择最优划分属性。划分过程中，决策树的分支结点所包含的样本尽可能属于同一类别，结点的“纯度”（purity）越来越高。

信息熵是度量样本集合纯度最常用的一种指标。
假定当前样本集合$D$中第$k$类样本所占的比例来为$p_k(k=1,2,...,|y|)$，则$D$的信息熵定义为
$$Ent(D)=-\sum _{k=1}^{|y|}{p}_{k}lo{g}_2{p}_k$$
$Ent(D)$的值越小，则$D$的纯度越高。

2.信息增益（Information gain）- ID3决策树

假定离散属性$a$有$V$个可能的取值$\{a^1,a^2,...,a^V\}$，若使用$a$来对样本集$D$进行划分，则会产生$V$个分支结点，其中第$v$个分支结点包含了$D$中所有在属性$a$上取值为$a^v$的样本，即为$D^v$。

给分支结点赋予权重$\frac{|D^v|}{|D|}$，样本数越多的分支结点的影响越大，信息增益越大，使用属性a对样本集$D$进行划分所获得的纯度提升越大。
$$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)$$

ID3（Iterative Dichotomiser，迭代二分器）决策树学习算法，以信息增益准则来选择划分属性。
信息增益准则对可取值数目较多的属性有所偏好。
从属性集A中选择最优划分属性$a_{\ast }=\underset{a\in A}{argmax}Gain(D,a)$。

3.增益率（Gain Ratio）- C4.5决策树

C4.5决策树算法不直接使用信息增益，而是使用增益率来选择最优划分属性。
增益率准则对可取值数目较少的属性有所偏好。
$$Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}$$
其中，$$IV(a)=-\sum _{v=1}^V\frac{|D^v|}{|D|}lo{g}_2\frac{|D^v|}{|D|}$$
称为属性a的固有值（Intrinsic Value）。属性a的可能取值数目越多，则$IV(a)$的值通常会越大。

C4.5决策树并未完全使用“增益率”代替“信息增益”，而是采用一种启发式的方法： 先选出信息增益高于平均水平的属性，然后再从中选择增益率最高的。

4.基尼指数（Gini Index）- CART决策树

CART（Classification and Regression Tree）决策树使用基尼指数来选择划分属性。
数据集$D$的纯度，用基尼值度量为：
$$Gini(D)=\sum _{k=1}^{|y|}\sum _{k^{\prime }\ne k}{p}_k{p}_k^{\prime }=1-\sum _{k=1}^{|y|}{p}_k^2$$
$Gini(D)$的值越小，则$D$的纯度越高。

属性a的基尼指数定义为：
$$Gini\_index(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D)$$
从属性集A中选择基尼指数最小的属性作为最优划分属性$a_{\ast }=\underset{a\in A}{argmin}Gini\_index(D,a)$。

5.剪枝处理（Pruning）

剪枝处理是决策树算法处理“过拟合”的主要方式，即主动去掉一些分支来降低过拟合的风险。

朋友们可以自己补一下<奥卡姆剃刀准则>。
从机器学习这本书中拿几张图，理解一下：

【西瓜数据集】未剪枝决策树流程图，选择属性“脐部”来对训练集进行划分判别西瓜的好坏。

决策树剪枝有两种基本策略：

（1）预剪枝（prepruning）

预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点。

（2）后剪枝（postpruning）

后剪枝是指先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。

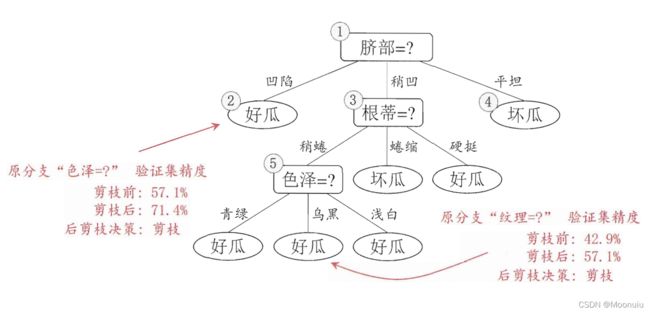
后剪枝决策树往往比预剪枝决策树保留更多的分支，一般情况下，后剪枝决策树的欠拟合风险较小，泛化能力往往优于预剪枝决策树。但后剪枝的训练时间比未剪枝和预剪枝都要长。

二、利用决策树进行鸢尾花数据集分类预测

sklearn中的决策树分类器

class sklearn.tree.DecisionTreeClassifier(*, criterion='gini', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, class_weight=None, ccp_alpha=0.0)

• criterion ： gini或者entropy，前者是基尼指数，后者是信息熵；
• max_depth ： int or None, optional (default=None) 设置决策随机森林中的决策树的最大深度，深度越大，越容易过拟合，推荐树的深度为：5-20之间；
• max_features： None（所有），log2，sqrt，N 特征小于50的时候一般使用所有的；
• max_leaf_nodes ： 通过限制最大叶子节点数，可以防止过拟合，默认是"None”，即不限制最大的叶子节点数。

数据集划分api

sklearn.model_selection.train_test_split(arrays, *options)

• 参数：
  x 数据集的特征值
  y 数据集的标签值
  test_size 测试集的大小，一般为float
  random_state 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
• return
  x_train, x_test, y_train, y_test

代码如下（示例）：

# pandas用于处理和分析数据
import pandas as pd
import numpy as np
# 导入鸢尾花数据集
from sklearn.datasets import load_iris
# 导入决策树分类器
from sklearn.tree import DecisionTreeClassifier
# # 导入分割数据集的方法
from sklearn.model_selection import train_test_split
# import relevant packages
from sklearn import tree
from sklearn.tree import export_text
# import matplotlib; matplotlib.use('TkAgg')
import matplotlib.pyplot as plt

# 利用决策树进行鸢尾花数据集分类预测
# 数据集字段说明：
# 特征值（4个）：sepal length（花萼长度），sepal width（花萼宽度）， petal length（花瓣长度），petal width（花瓣宽度）
# 目标值（3个）：target（类别，0为'setosa'山鸢尾花，1为'versicolor'变色鸢尾花，2为'virginica'维吉尼亚鸢尾花）

# load in the data加载数据
data = load_iris()
# convert to a dataframe 转换数据格式
df = pd.DataFrame(data.data, columns = data.feature_names)
# create the species column
df['Species'] = data.target

# replace this with the actual names
target = np.unique(data.target)  # 对于一维数组或者列表，unique函数去除其中重复的元素，并按元素由大到小返回一个新的无元素重复的元组或者列表
target_names = np.unique(data.target_names)
targets = dict(zip(target, target_names))
df['Species'] = df['Species'].replace(targets)

# extract features and target variables 提取特征和目标变量
x = df.drop(columns="Species")
y = df["Species"]
# save the feature name and target variables 保存特征名称和目标变量
feature_names = x.columns
labels = y.unique()  # 去除重复元素

# 分割训练集、测试集
# x 数据集的特征值
# y 数据集的标签值
# 训练集的特征值x_train 测试集的特征值x_test(test_x) 训练集的目标值y_train 测试集的目标值y_test(test_lab)
# random_state 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
X_train, test_x, y_train, test_lab = train_test_split(x,y,
                                                 test_size = 0.4,
                                                 random_state = 42)
# 创建决策树分类器（树的最大深度为3）
model = DecisionTreeClassifier(max_depth =3, random_state = 42)  # 初始化模型
model.fit(X_train, y_train)  # 训练模型
print(model.score(test_x,test_lab))  # 评估模型分数
# 计算每个特征的重要程度
print(model.feature_importances_)

# 可视化特征属性结果
r = export_text(model, feature_names=data['feature_names'])
print(r)

# plt the figure, setting a black background
plt.figure(figsize=(30,10), facecolor ='g')  # facecolor设置背景色

# create the tree plot 决策树绘图模块，实现决策树可视化
a = tree.plot_tree(model,
                   # use the feature names stored
                   feature_names = feature_names,
                   # use the class names stored
                   class_names = labels,
                   # label='all',
                   rounded = True,
                   filled = True,
                   fontsize=14,
                   )
# show the plot
# plt.legend(loc='lower right', borderpad=0, handletextpad=0)
plt.savefig("save.png", dpi=300, bbox_inches="tight")
# plt.tight_layout()
plt.show()

输出结果：

0.9833333333333333
[0.         0.         0.58908421 0.41091579]
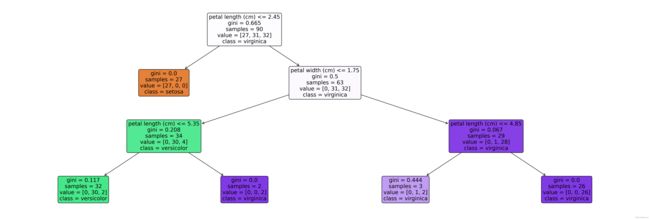
|--- petal length (cm) <= 2.45
|   |--- class: setosa
|--- petal length (cm) >  2.45
|   |--- petal width (cm) <= 1.75
|   |   |--- petal length (cm) <= 5.35
|   |   |   |--- class: versicolor
|   |   |--- petal length (cm) >  5.35
|   |   |   |--- class: virginica
|   |--- petal width (cm) >  1.75
|   |   |--- petal length (cm) <= 4.85
|   |   |   |--- class: virginica
|   |   |--- petal length (cm) >  4.85
|   |   |   |--- class: virginica