机器学习 主成分分析（Principal Component Analysis）

1 什么是主成分分析

主成分分析法是一个非监督学习的机器学习算法，主要用于数据的降维，对于高维数据，通过降维，可以发现更便于人类理解的特征。这里我们还是从二维数据去开始理解：

当我们对高维数据降低到低维数据时，我们就要把多个轴合成一个轴，如果我们相对上图中的数据进行降维使其变为一维，如果我们直接将其映射到其中一个轴上时，会丢掉太多的信息，我们的任务就是在数据降维的同时还要保留尽可能多的信息，于是我们找到了上图中红线作为我们降维之后的坐标轴，那我们是如何找到这个让样本间间距最大的轴呢？

首先我们要去思考如何定义样本间间距？我们使用的属性是方差（Variance）：$$Var(x)=\frac{1}{m}\sum (x_i-\overline{x}{)}^2$$这里我们就要思考方差的属性，方差是刻画数据之间的差别的，方差越大，波动就越大，在这里正好可以起到我们想要去保存数据“波动”的作用，也就是最大程度保存了数据的差异。那么我们的任务就明确了，找到一个轴，使样本空间的所有点映射到这个轴后，方差最大。

在PCA算法中，第一步我们需要将样例的均值归为0，这步操作被称为数据中心化(demean)操作：

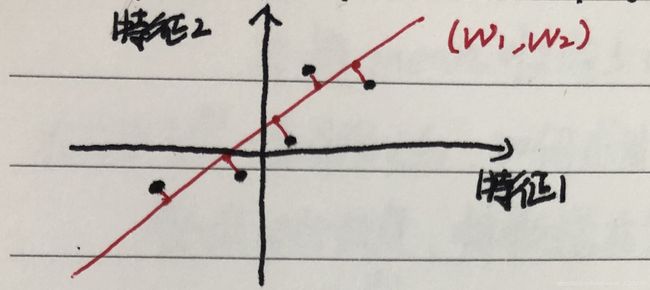
也就是变换完成以后数据中的点与坐标轴之间的关系会变成类似上图中的关系，这一步的操作主要是为了在之后得到协方差矩阵而做铺垫，这是方差：$$Var(x)=\frac{1}{m}\sum _{i=1}^m(X_i-\overline{X}{)}^2且\overline{X}=0$$$$Var(x)=\frac{1}{m}\sum _{i=1}^m{X}_i^2$$也就是我们对所有的样本进行了demean处理之后，我们想要求一个轴的方向$\omega =({\omega }_1,{\omega }_2)$，使得我们所有的样本，映射到$\omega$以后，使下式的值最大（这里的$X_{project}$是映射后的X）：$$Var(X_{project})=\frac{1}{m}\sum _{i=1}^m|X_{project}^{(i)}{|}^2=\frac{1}{m}\sum _{i=1}^m(X^{(i)}\cdot \omega {)}^2$$到这里以后，PCA的正规方程解如下：


同时这里PCA完整的数学推导：https://zhuanlan.zhihu.com/p/77151308

也就是说，PCA 的算法步骤：
1）将原始数据按列组成 n 行 m 列矩阵 X；
2）将 X 的每一行进行零均值化，即减去这一行的均值；
3）求出协方差矩阵$C=\frac{1}{m}X{X}^T$；
4）求出协方差矩阵的特征值及对应的特征向量；
5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前 k 行组成矩阵 P；
6）$Y=PX$即为降维到 k 维后的数据。

2 实现自己的PCA算法

在上一节中我们的目标是求得$\omega$，使得下式最大：$$Var(X_{project})=\frac{1}{m}(X^{(i)}\cdot \omega {)}^2$$在这里自己实现时不使用协方差矩阵，我采用梯度上升法即：$$Var(X_{project})=\frac{1}{m}(X_1^{(i)}\cdot {\omega }_1+X_2^{(i)}\cdot {\omega }_2+...+X_n^{(i)}\cdot {\omega }_n{)}^2$$上式作为效用函数，前两章我们都是去最小化一个损失函数，这次我们要最大化一个效用函数，同理使用梯度上升法去搜索参数：$$▽f=\left[\begin{array}{c}\frac{\alpha f}{\alpha {\omega }_1}\\ \frac{\alpha f}{\alpha {\omega }_2}\\ ...\\ \frac{\alpha f}{\alpha {\omega }_n}\end{array}\right]=\frac{2}{m}\left[\begin{array}{c}{\sum }_{i=1}^m(X^{(i)}\cdot \omega )X_1^{(i)}\\ {\sum }_{i=1}^m(X^{(i)}\cdot \omega )X_2^{(i)}\\ .....\\ {\sum }_{i=1}^m(X^{(i)}\cdot \omega )X_n^{(i)}\end{array}\right]=\frac{2}{m}{X}^T(X\omega )$$最后的结果是向量化后的结果。现在可以用来创建我们自己的PCA算法：

这里我们生成一个模拟的数据集并加上一些噪音：

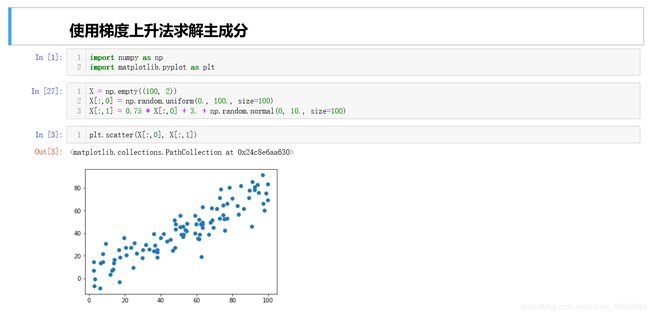
按照我们之前提到的步骤进行demean数据中心化处理：

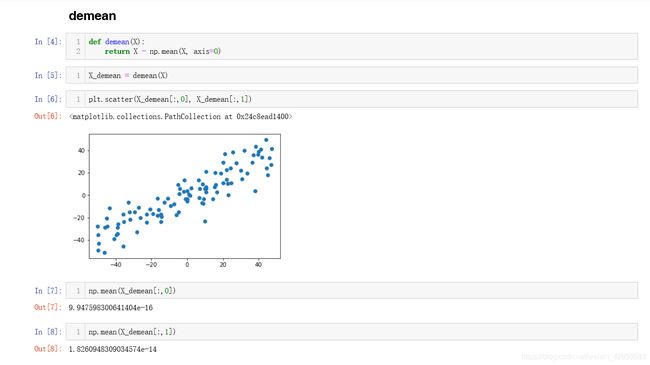
稍微改善我们之前的梯度下降法的代码，使梯度下降改为攀升即可：


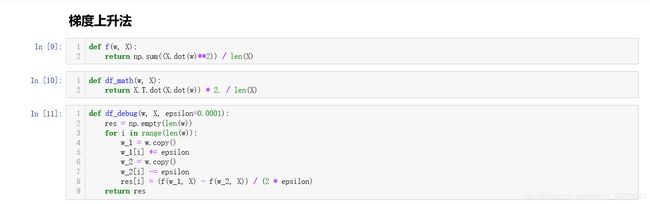
在我们使用梯度上升法得到数据时，绘制出来投影轴来观察一下：

这时假如我们的数据不带有任何噪音，验证一下我们的算法是否正确：

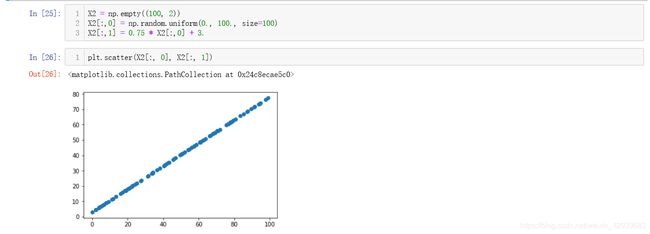
绘制出来投影后的主成分可以观察出来我们的算法没有错误：

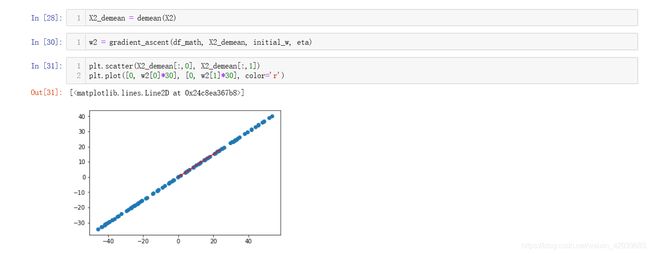
在用梯度上升法去实现PCA时有几点需要注意：
1）在我们实现梯度上升法时，$\omega$本身是单位方向向量加上步长之后要再对其单位化，不进行单位化并不是错误，如果不进行单位化会使$\omega$增加较快，这样我们就不得不去降低学习率$\eta$去增加迭代次数，会导致效率的降低。
2）在初始化inital_w时我们不能再像下降法一样从0开始，第一使我们求梯度公式中$\omega$取0向量会使结果仍是0，齐次是0向量表示方向正是极值点。
3）我们不能在使用梯度上升法之前去使用Standard Scaler标准化数据，因为我们的效用函数本身就是基于方差去运算求解，标准化数据之后映射方差就会为1，其实我们之前进行demean操作完成了标准化数据的一半，只将mean归成了0而不去处理方差。

上面这些步骤我们只是求出了第一主成分，如何求出下面的主成分？我们要对数据进行改变，将数据在第一个主成分上的分量去掉：

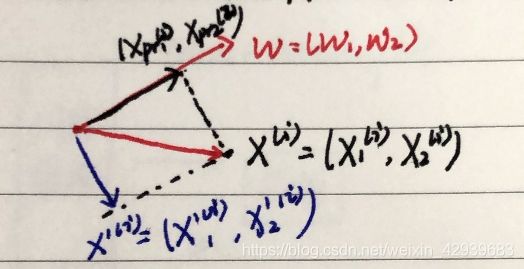
$$X^{(i)}\cdot \omega =|X_{project}^{(i)}|$$$$X_p^{(i)}roject=|X_{project}^{(i)}|\cdot \omega$$$$X^{\prime (i)}=X^{(i)}-X_{project}^{(i)}$$其中$X^{\prime }$使我们舍弃的分量，$X_{project}$使我们提取出主成分后的分量，也就是我们每一次提取出主成分后将主成分在我们的数据中进行剔除，在提取下一个主成分：

这里我们还是生成一个模拟数据：


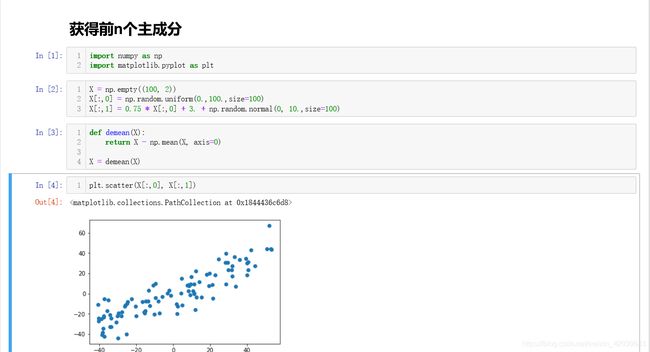
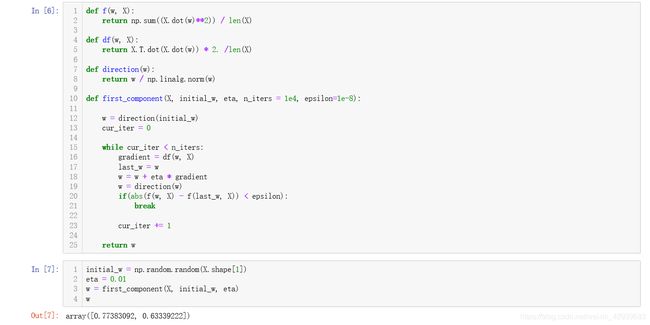
当我们提取出第一个主成分后可视化一下$X^{\prime }$：


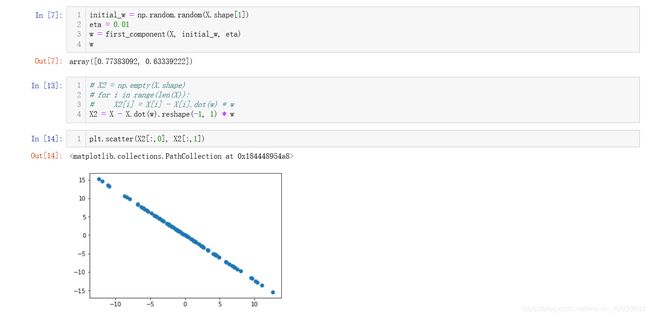
从结果就可以看出提取出来的主成分是正交的，实质上也就是我们在使用协方差矩阵计算时我们要把协方差矩阵进行SVD分解，得到一个对角阵和其特征向量，这样每一个主成分也就是特征向量都是正交的，这里我们使用梯度上升法也可以印证这一点。

在求出前几个主成分之后，如何对数据进行降维，也就是我们要实现高维数据向低维数据的映射：

我们有样本：$$X=\left[\begin{array}{cccc}{X}_1^{(1)}& X_2^{(1)}& ...& X_n^{(1)}\\ X_1^{(2)}& X_2^{(2)}& ...& X_n^{(2)}\\ ....& ....& ...& ....\\ X_1^{(m)}& X_2^{(m)}& ...& X_n^{(m)}\end{array}\right]$$同时我们有前k个主成分的方向向量：$${\omega }_k=\left[\begin{array}{cccc}{\omega }_1^{(1)}& {\omega }_2^{(1)}& ...& {\omega }_n^{(1)}\\ {\omega }_1^{(2)}& {\omega }_2^{(2)}& ...& {\omega }_n^{(2)}\\ ....& ....& ...& ....\\ {\omega }_1^{(k)}& {\omega }_2^{(k)}& ...& {\omega }_n^{(k)}\end{array}\right]$$每一行都是一个主成分，我们若将x中的一个样本点称w_k可以得到这个样本在w_k下表示的样本点。也就是：$$X\cdot {\omega }_k^T=X_k$$将n维数据降维到了k维，需要注意的是当向k维映射后数据就丢失了一部分，再使用$X_k\cdot {\omega }_k=X^{\prime }$并原先的X了。下面我们就可以实现自己的PCA算法：

import numpy as np

class PCA:

    def __init__(self, n_components):
        """初始化PCA"""
        assert  n_components >= 1, "n_components must be valid"
        self.n_components = n_components
        self.components_ = None

    def fit(self, X, eta=0.01, n_iters=1e4):
        """获得数据集X的前n个主成分"""
        assert self.n_components <= X.shape[1], \
            "n_components must not be greater than the feature number of X"

        def demean(X):
            return X - np.mean(X, axis=0)

        def f(w, X):
            return np.sum((X.dot(w) ** 2)) / len(X)

        def df(w, X):
            return X.T.dot(X.dot(w)) * 2. / len(X)

        def direction(w):
            return w / np.linalg.norm(w)

        def first_component(X, initial_w, eta=0.01, n_iters=1e4, epsilon=1e-8):

            w = direction(initial_w)
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = df(w, X)
                last_w = w
                w = w + eta * gradient
                w = direction(w)
                if(abs(f(w, X) - f(last_w, X)) < epsilon):
                    break

                cur_iter += 1

            return w

        X_pca = demean(X)
        self.components_ = np.empty(shape=(self.n_components, X.shape[1]))
        for i in range(self.n_components):
            initial_w = np.random.random(X_pca.shape[1])
            w = first_component(X_pca, initial_w, eta, n_iters)
            self.components_[i,:] = w

            X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w

        return self

    def transform(self, X):
        """将给定的X,映射到各个主成分分量中"""
        assert X.shape[1] == self.components_.shape[1],\
            "must fit before transform"

        return X.dot(self.components_.T)

    def inverse_transform(self, X):
        """将给定的X，反向映射回原来的特征空间中"""
        assert X.shape[1] == self.components_.shape[0]

        return X.dot(self.components_)

    def __repr__(self):
        return "PCA(n_components=%d)" % self.n_components

下面让我们来看一下降维数据，还是先生成模拟数据：

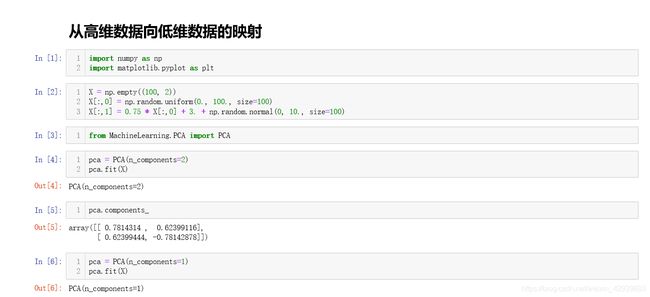
下面我们按照上面的方法我们把高维数据映射到低维再恢复过来：

从结果就可以看出，如果先降维再回复只会保留在主成分上的信息，相当于除去了一些信息，之后我们可以将这一方法用于降噪，我们看一下sklearn中的PCA:


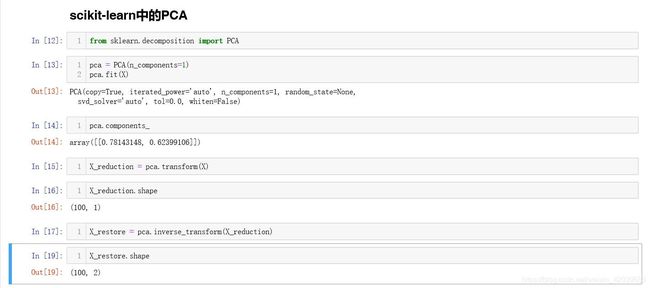
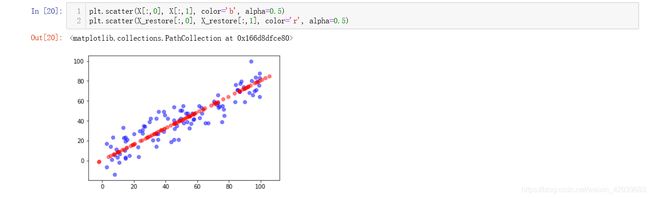
使用一样的逻辑可以得到相同的结果，虽然我们的效率低一些但是达到了相同的目的。

3 scikit-learn中的PCA

我们使用sklearn中的PCA作用于真实的手写识别数据：

可见原本数据有64个维度，我们如果不对其降维直接进行knn算的训练，可以看到花费了6毫秒达到了0.96的精度，下面我们把它们降维到只有两个维度，也就是得到两个主成分：

从结果可以看到速度是快了很多但是精度也下降将了很多，这是由于我们丢失的信息太多了，在sklearn中PCA有一个属性explain_variance_ratio_，这个属性可以看出我们的主成分可以解释多少的方差特征，从上面的结果我们可以看到第一个主成分可以解释14%的方差属性，第二个主成分可以解释13%的方差属性，也就是说我们将数据降到了二维丢失了大概73%的数据，于是我们想得到精度更高的数据，那我们将64个主成分的解释的方差信息都列出来：

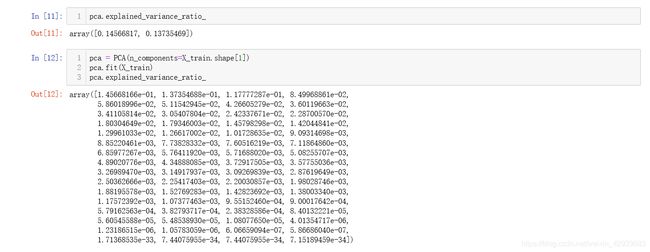
可以看到在最后的主成分占有的比例量级达到了10的负35次方，显然这些使我们不需要的，于是我们画一个图：

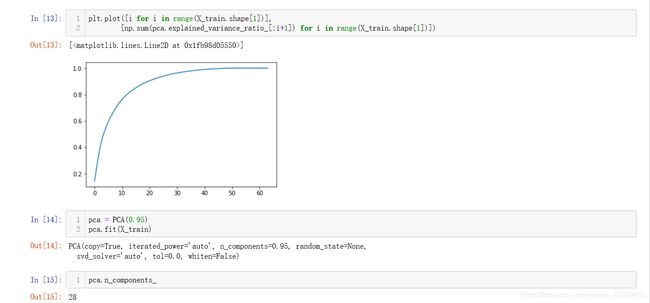
通过上面的绘图就可以看到我们使用的主成分越多精度也就越高，但是越往后会越缓慢，sklearn中提供了方法我们可以直接传入我们需要的精度，也就是保留了多少方差信息，我们这里传入95%，从结果可以看到选取了前28个主成分。

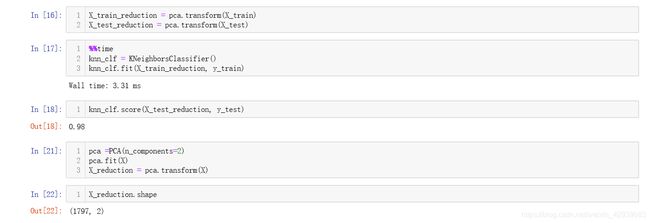
这时我们用前28个主成分降维，时间缩短了一倍，而精度我们只损失了1%，已经是很好的情况了，但我们降到二维的数据并不是一点作用都没有的，二维数据优点就是可以可视化：

可见虽然我们仅仅使用了前两个主成分就已经可以看出大概的区别了，假如我们的任务是分离蓝色和灰色的点，那二维数据反而效果就已经很好了。

从上面这个例子可能看不出来PCA算法的优势，现在我们换一个更大的数据集，手写识别MNIST数据集：

可以看到这个训练数据集有784个样本特征，下面我们不降维使用knn算法训练：

可以看到我们训练花费了27秒，测试用了20分钟（吐血），下面我们使用PCA降维后：

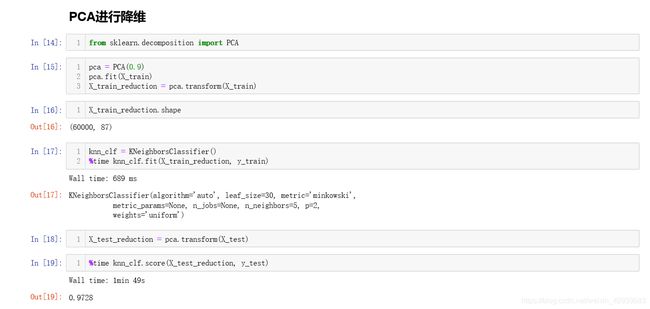
降维以后我们仅仅保留90%的数据信息，取出了87个主成分，无论是训练时间还是测试时间都减少了10倍以上甚至更多，并且从结果看出来分类的精度还提高了？这是为什么呢？就像之前说的一样，虽然PCA算法丢失了一些信息，但是那些信息不属于主成分上可能就是噪音，所以PCA算法还可以用来降噪：

这里还是使用sklearn中的手写识别例子，我们以一种可视化的方式去看一下我们的数据：

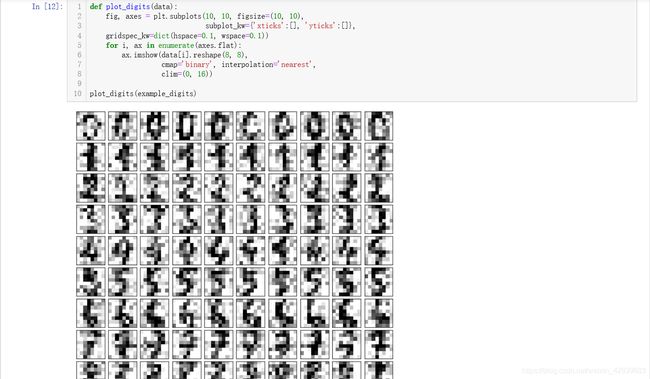
可以看到虽然模糊但是还是可以用肉眼识别出来的，下面我们使用PCA降噪：


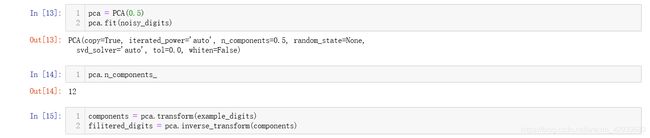
从结果单凭肉眼就可以看出下面可视化的图片更容易识别出来，这也说明了PCA的优势，噪音仅仅可能存在在部分样本数据中，但是PCA算法的任务就是选出样本间的最大的共通性，也就是选出最大的特点。

上面我们从样本$X$中得到了$\omega$主成分矩阵，实质上每一个特征对于协方差矩阵的特征向量，在人脸识别中，特征向量可以帮助我们绘制特征脸：





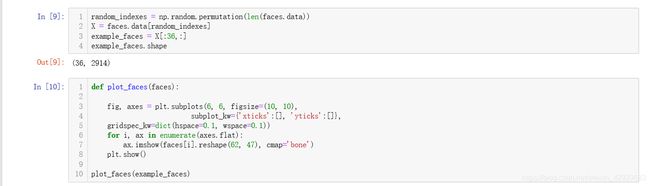
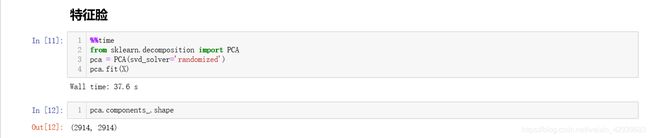
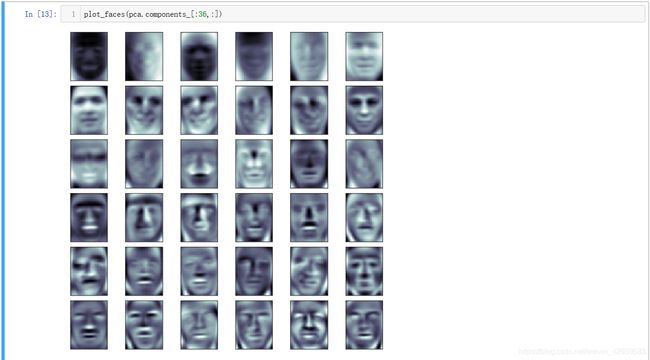
这里我只介绍一下PCA用于人脸识别的一个例子，这个例子分离出来的特征脸我们可以看出每一个特征实质上都代表了人脸的一些属性，也就是说我们训练的样本都可以表示为这些特征脸的一些线性组合，那么我们使用不同的线性组合是不是还可以生成一个不存在的人但是确确实实有他的人脸图像呢？嘿嘿，其实我也不懂，但是科学就是这样的奇妙，希望大家可以继续深入学习，大家加油！