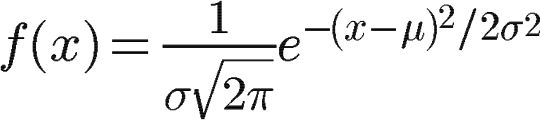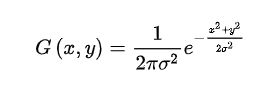图像处理：高斯滤波

高斯滤波

　　高斯滤波（也可以说“高斯模糊”）其实就是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。简单来说就是整个图像某个像素点的值与周围像素点的值挂钩，是原图像某一像素点的值其实是其本省和周围像素点值的加权平均过程。

　　处理结果上：整个图像相较于原图像会看起来较为模糊，原图像上的某些噪声点在经过周围像素点加权求和后会被剔除掉。

下面这个是看到很有意思的两张图：

                        图1　高斯　　　　　　　　　　　　　　图2 高斯滤波

什么时候需要用到高斯滤波？

　　答：原图像上存在很多和周围像素差距过大的像素点，这种噪声点可能会对之后搜索图像关键因素产生干扰的情况。当然，也可以不用高斯滤波，可以采用其他处理，反正就是怎么处理合适怎么来就好。

---

实现

　　现在经过初步了解什么是高斯滤波之后，下面说说怎么实现高斯滤波。

　　1、初步计算

　　之所以被冠以“高斯”之名，是因为处理过程里面，运用了高斯函数，也就是：

                  

　　其中：μ是x的均值，σ是x的标准差。μ决定了分布对称中心，σ决定了分布的形状（σ越小形状越瘦）。

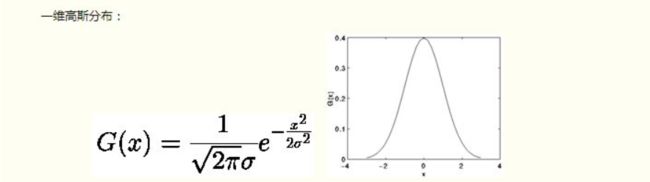
　　　　　　　　　　　　　　　　　　图3 一维高斯分布图像

　　高斯公式在图像上，是一种钟形图像。也就是越接近像素点，对该像素点的影响越大。

　　而每次计算都是以当前像素点计算，因此周围坐标的均值μ其实就是0。因此将公式简化：       

　　现在假定一组一维像素点，σ = 1.5：

相对像素点坐标	-1	0（中心坐标点）	1
像素值	126	230	124

　　我们将像素坐标带入高斯公式中，将得到（高斯公式的值与像素点的值无关，因此先忽略）：

相对像素点坐标	-1	0	1
计算值	0.212965	0.265962	0.212965

　　你可以将计算出的值理解为该相对位置“权重”，而这个“权重”与像素点的值无关。因此我们可以以这个为模板，事先计算出我们定好σ以及半径后的各位置对应的值作为模板。这样我们就能大大节约运算时间，不必每次都重新计算。

　　2、归一化

　　但为了接下来方便计算，我们还可以进行一个操作：归一化。

　　为什么归一化呢？在加权求和时，最终的结果我们还需要除以权重和。而我们将这计算的和先除掉，其实并不影响之后的结果。

　　接下来，将得到的计算值求和：0.691892。将个计算值除这个和，我们就将得到真正的权重。

相对像素点坐标	-1	0	1
最终结果	0.307801	0.384398	0.307801

　　这个得到的结果也可以被称为：高斯掩膜。

　　之后将像素点的值计算之后我们就能得到处理后的中心坐标像素点了：126*0.307801+230*0.384398+124*0.307801=165.36179。

　　根据结果看：中心像素点过高的值明显被拉低了。

　3、扩展二维

　　（1）运算

　　对一维处理我们知道是怎么回事了，但图像并不是一维的，我门还需学习二维的处理。

　　下面是二维的高斯公式和分布图像。

 　　　　　　　　　　　　　　　　 图4  二维高斯分布图像

　　其实二维只是将一维坐标换为了二维坐标。根据一维的结论，我们就知道只需要事先求一个二维的高斯掩码就可以了，这里就不求了。

　　我们计算某像素点的值，其实就还需要将周围点的值乘对应位置的高斯掩码，最后求和就好。

　　（2）优化算法

　　这么看来二维和一维差不了多少，但是接下来才是二维需要关注的点：优化算法。

　　假设是一个7*7的一个高斯掩码。那我们处理一张图像，那最起码要遍历49次图像（每个像素点都需要遍历周围48个像素点），这样来看耗时就会多很多。对于一些需要及时处理的情况无疑是致命的。

　　那有什么好的方法能减少处理时长呢？有！将二维的处理转换为一维的处理。这其实是一个很简单的过程。

　　这是二维的公式：                                   

　　那么我们经过简单的数学变换：                                   

　　我们就得到一个结论：可以将二维变换拆解为两个一维变化。

　　也就是说我们将原图像经过一次x方向，一次y方向的一维变化后的效果与一次二维变化后的效果是一样的。而遍历次数则变为了14次（x方向遍历7次，y方向遍历7次），极大缩减了处理时长。

---

程序　

　　以下是一个使用C语言的简单高斯图像处理函数：

复制代码
/**
 * @fileOverview    高斯模糊
 * @prama sigma 标准差
 * @prama radius 模糊半径
 * @author 
 * @since
 */
void fileOverview(uint8 radius,float sigma)
{
    float gaussMatrix[2*radius+1];//模板数组
    float gaussSum=0;　　

　　//高斯公式中的两部分
    float a=1/(sqrt(2*3.14159));
    float b=-1/(2*sigma*sigma);

　　uint8 image[MTV03X_H][MTV03X_W];//和原图像相同的数组，MTV03X_H为图像高，MTV03X_w为图像宽
    //计算高斯矩阵
    float sum=0;//求和用于归一化
    for(int i=-radius;i<=radius;i++){
        gaussMatrix[i+radius]=a*exp(b*i*i);
        sum +=gaussMatrix[i+radius];
    }

    //归一化
    for(int i=-radius;i<=radius;i++)
    {
        gaussMatrix[i+radius]=gaussMatrix[i+radius]/sum;
    }

    //x方向一维运算
    for(int y=0;y=0)&&(x+j=0)&&(y+j

希望本篇文章能够对你有所帮助，如有错误请指正。

原文：图像处理：高斯滤波 - ailaopo_zhai - 博客园 (cnblogs.com)