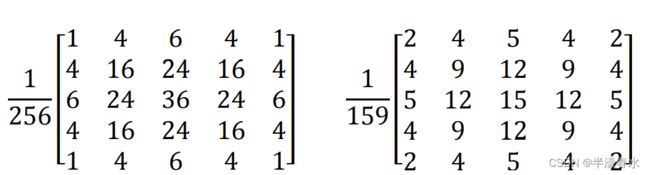高斯滤波(Gauss filtering)
1.概念介绍
高斯滤波是一种
线性平滑滤波,适用于消除高斯噪声,广泛应用于图像处理的减噪过程。
通俗的讲,高斯滤波就是对整幅图像进行加权平均的过程,每一个像素点的值,都由其本身和邻域内的其他像素值经过加权平均后得到。
高斯滤波的具体操作是:用一个模板(或称卷积、掩模)扫描图像中的每一个像素,用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。
对应均值滤波和方框滤波来说,其邻域内每个像素的权重是相等的。而在高斯滤波中,会将中心点的权重值加大,远离中心点的权重值减小,在此基础上计算邻域内各个像素值不同权重的和。2.基本原理
在高斯滤波中,卷积核的值不再是1。例如,一个3×3的卷积核可能如图2-1所示。
图2-1 高斯滤波卷积核示例
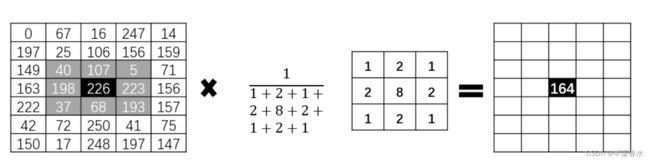
在图2-2中,针对最左侧的图像内第4行第3列位置上像素值为226的像素点进行高斯卷积,其运算规则为将该领域内的像素点按照不同的权重计算和。
图2-2 高斯卷积示例
在实际计算时,使用的卷积核如图2-3中的卷积核所示。
图2-3 实际计算中的卷积核
使用图2-3中的卷积核,针对第 4 行第 3 列位置上的像素值为 226 的像素点进行高斯滤波处理,计算方式为:
新值=(40×0.05+107×0.1+5×0.05)
+(198×0.1+226×0.4+223×0.1)
+(37×0.05+68×0.1+193×0.05)
=164
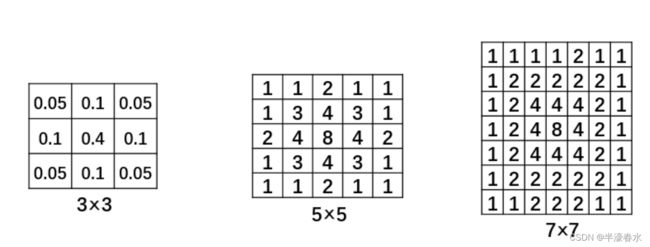
在实际使用中,高斯滤波使用的可能是不同大小的卷积核。例如,图2-4中分别是 3×3、5×5、7×7 大小的卷积核。在高斯滤波中,核的宽度和高度可以不相同,但是它们都必须是奇数。
图2-4 不同大小的卷积核
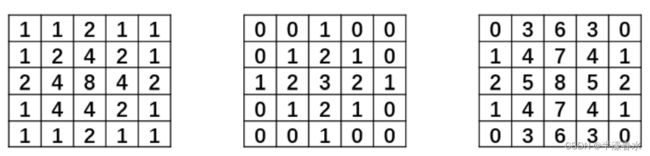
每一种尺寸的卷积核都可以有多种不同形式的权重比例。例如,同样是5×5的卷积核,可能是图2-5中所示的两种不同的权重比。
图2-5 同一尺寸的卷积核可以有不同的权重比
在实际计算中,卷积核是归一化处理的,这种处理可以表示为图2-4最左侧的小数形式的卷积核,也可以表示为如图2-5所示的分数形式。
也要注意,在一些资料中,给出的卷积核并没有进行归一化,这时的卷积核可能表示为图2-4中间和右侧所示的卷积核,这样的卷积核是为了说明问题用的,实际使用时往往需要进行归一化。严格来讲,使用没有进行归一化处理的卷积核进行滤波,得到的结果往往是错误的。3.函数语法
在 OpenCV 中,实现高斯滤波的函数是
cv2.GaussianBlur(),该函数的语法格式是:
dst = cv2.GaussianBlur( src, ksize, sigmaX, sigmaY, borderType )
参数解析:
dst:返回值,表示进行高斯滤波后得到的处理结果。
src: 是需要处理的图像,即原始图像。它能够有任意数量的通道,并能对各个通道独立处理。图像深度应该是 CV_8U、CV_16U、CV_16S、CV_32F 或者 CV_64F 中的一种。
ksize: 是滤波核的大小。滤波核大小是指在滤波处理过程中其邻域图像的高度和宽度。需要注意,滤波核的值必须是奇数。
sigmaX:卷积核在水平方向上(X 轴方向)的标准差,其控制的是权重比例。如下图2-5 中是不同的 sigmaX 决定的卷积核,它们在水平方向上的标准差不同。
图2-5 不同的 sigmaX 决定的卷积核
sigmaY:卷积核在垂直方向上(Y 轴方向)的标准差。如果将该值设置为 0,则只采用sigmaX 的值;如果 sigmaX 和 sigmaY 都是 0,则通过 ksize.width 和 ksize.height 计算得到。其中:
sigmaX = 0.3×[(ksize.width-1)×0.5-1] + 0.8
sigmaY = 0.3×[(ksize.height-1)×0.5-1] + 0.8
borderType:边界样式,该值决定了以何种方式处理边界。一般情况下,不需要考虑该值,直接采用默认值即可。
在该函数中,sigmaY 和 borderType 是可选参数。sigmaX 是必选参数,但是可以将该参数设置为 0,让函数自己去计算 sigmaX 的具体值。4.程序示例
针对一幅噪声图像进行高斯滤波,显示滤波的结果。
import cv2
Gn=cv2.imread("Gaussian_noise.jpg")
Gf=cv2.GaussianBlur(Gn,(3,3),0,0)
cv2.imshow("噪声图像",Gn)
cv2.imshow("高斯滤波处理结果图像",Gf)
cv2.waitKey()
cv2.destroyAllWindows()
程序运行后,其中图4-1是噪声图像,图4-2是高斯滤波后的处理结果图像。
图4-1 噪声图像
图4-2 高斯滤波处理结果图像