【机器学习】高斯混合聚类python实现
高斯混合聚类算法的原理如下:
由于在对数函数里面又有加和,我们没法直接用求导解方程的办法直接求得最大值。为了解决这个问题,我们采取之前从 GMM 中随机选点的办法:分成两步,实际上也就类似于 K-means 的两步。
下面用西瓜数据集4.0版本实现算法:数据集watermelon4.txt如下:
Python实现如下:
from numpy import *
import numpy as np
import matplotlib.pyplot as plt
# 高斯混合聚类
# 预处理数据
def loadData(filename):
dataSet = []
fr = open(filename)
for line in fr.readlines():
curLine = line.strip().split('\t')
fltLine = list(map(float, curLine))
dataSet.append(fltLine)
return dataSet
# 高斯分布的概率密度函数
def prob(x, mu, sigma):
n = shape(x)[1]
expOn = float(-0.5*(x-mu)*(sigma.I)*((x-mu).T))
divBy = pow(2*pi, n/2)*pow(linalg.det(sigma), 0.5)
return pow(e, expOn)/divBy
# EM算法
def EM(dataMat, maxIter=50):
m, n = shape(dataMat)
# 初始化各高斯混合成分参数
alpha = [1/3, 1/3, 1/3]
mu = [dataMat[5, :], dataMat[21, :], dataMat[26, :]]
sigma = [mat([[0.1, 0], [0, 0.1]]) for x in range(3)]
gamma = mat(zeros((m, 3)))
for i in range(maxIter):
for j in range(m):
sumAlphaMulP = 0
for k in range(3):
gamma[j, k] = alpha[k]*prob(dataMat[j, :], mu[k], sigma[k])
sumAlphaMulP += gamma[j, k]
for k in range(3):
gamma[j, k] /= sumAlphaMulP
sumGamma = sum(gamma, axis=0)
for k in range(3):
mu[k] = mat(zeros((1, n)))
sigma[k] = mat(zeros((n, n)))
for j in range(m):
mu[k] += gamma[j, k]*dataMat[j, :]
mu[k] /= sumGamma[0, k]
for j in range(m):
sigma[k] += gamma[j, k]*(dataMat[j, :]-mu[k]).T*(dataMat[j, :]-mu[k])
sigma[k] /= sumGamma[0, k]
alpha[k] = sumGamma[0, k]/m
#print(mu)
return gamma
# init centroids with random samples
def initCentroids(dataMat, k):
numSamples, dim = dataMat.shape
centroids = zeros((k, dim))
for i in range(k):
index = int(random.uniform(0, numSamples))
centroids[i, :] = dataMat[index, :]
return centroids
def gaussianCluster(dataMat):
m, n = shape(dataMat)
# 每个样本的所属的簇,以及分到该簇对应的响应度
## step 1: init centroids
centroids = initCentroids(dataMat, m)
clusterAssign = mat(zeros((m, 2)))
gamma = EM(dataMat)
for i in range(m):
# amx返回矩阵最大值,argmax返回矩阵最大值所在下标
clusterAssign[i,:] = argmax(gamma[i, :]), amax(gamma[i, :])
## step 4: update centroids
for j in range(m):
pointsInCluster = dataMat[nonzero(clusterAssign[:, 0].A == j)[0]]
centroids[j, :] = mean(pointsInCluster, axis = 0)
return centroids,clusterAssign
def showCluster(dataMat, k, centroids, clusterAssment):
numSamples, dim = dataMat.shape
if dim != 2:
print("Sorry! I can not draw because the dimension of your data is not 2!")
return 1
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ' len(mark):
print("Sorry! Your k is too large!")
return 1
# draw all samples
for i in range(numSamples):
markIndex = int(clusterAssment[i, 0])
plt.plot(dataMat[i, 0], dataMat[i, 1], mark[markIndex])
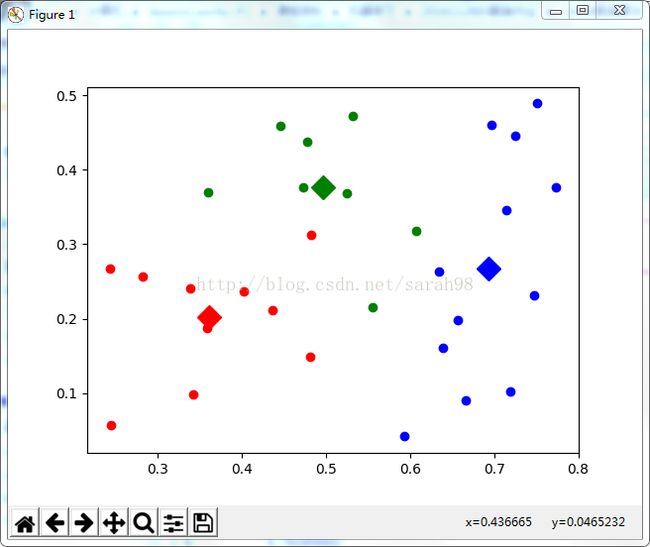
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', ' 第10轮迭代效果图
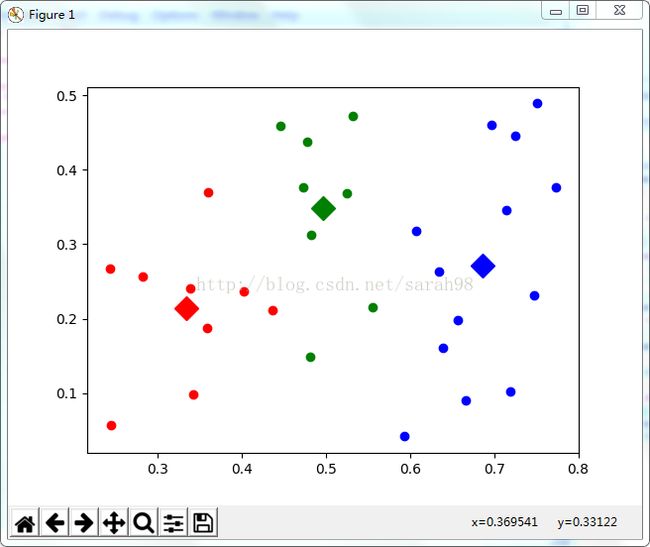
第20轮迭代效果图
第50轮迭代效果图