深度学习入门笔记3 自适应神经元

自适应线性神经元

概念

自适应线性神经网络（ADALINE——Adaptive Linear Neuron）是在感知器的基础上进行的一种改进。激活函数采用线性连续的函数来代替阶跃函数。

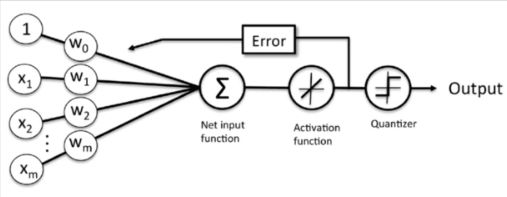
自适应神经元&感知器

• 激活函数：自适应神经元使用线性激活函数，感知器使用阶跃函数。
• 误差更新：自适应神经元在最终结果前进行更新，感知器在最终结果后进行更新。
• 损失函数：自适应神经元使用SSE最为损失函数，感知器没有损失函数。
• 应用：自适应神经元可以进行分类与回归（可以输出连续值或离散值），感知器不能进行回归。

计算公式

$z=w1\ast x1+w2\ast x2+\dots \dots +wn\ast xn+b={\sum }_{j=1}^{n}wj\ast xj=w^T\ast x+b$
令$x0=1，w0=b$，则：
$z={\sum }_{j=0}^{n}wj\ast xj$
净输入z经过激活函数f进行激活，得到结果a，这里的a即为预测的输出值$\hat{y}$。
$a=f(z)$
损失函数为：
$J(w)={\sum }_{i=1}^n\frac{1}{2}(y^{(i)}-{\hat{y}}^{(i)}{)}^2$
计算梯度，最终权重的更新为：
$\Delta wj=\eta (y^{(i)}-{\hat{y}}^{(i)})f^{\prime }(z)x_j^{(i)}$
特别的，如果使用y = x激活函数，则权重更新为：
$\Delta wj=\eta (y^{(i)}-{\hat{y}}^{(i)})x_j^{(i)}$

import numpy as np
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

class AdaLine:
    """Python实现自适应线性神经网络。使用批量梯度下降调整权重。"""
    
    def __init__(self, alpha, times):
        """初始化方法。
        
        Parameters
        ------
        alpha : float
            学习率。
        times : int
            对数据集进行多少轮的迭代（epoch）。
        """
        self.alpha = alpha
        self.times = times
    
    # 批量梯度下降
    def fit(self, X, y):
        """使用指定的样本与标签进行训练。得到一个合适的权重值。
        
        Parameters
        -----
        X : 类数组类型。形状：(样本数量， 特征数量)
            提供训练的样本数据。
        y : 类数组类型。形状：(样本数量,)。
            样本对应的标签。
        """
        X = np.asarray(X)
        y = np.asarray(y)
        # 对权重进行初始化（初始化为0），此处将w与b分开处理（w的长度与特征的长度相同）。
        self.w_ = np.zeros(shape=(X.shape[1], 1))
        # 对偏置进行初始化。
        self.b_ = 0
        # 定义损失列表。用来保存每次数据集迭代过程中的损失值。
        self.cost_ = []
        # 进行迭代
        for _ in range(self.times):
            # 注意：感知器的时候，我们是对每一个样本进行的处理，但是，这里，我们
            # 使用批量梯度下降，是针对整个数据集计算梯度。
#             for x, target in zip(X, y):
            # 计算净输入。
            net_input = np.dot(X, self.w_) + self.b_
            # 将净输入传入激活函数。得到输出。这里的a就相当于是y_hat。
            a = self.activation(net_input)
            # 计算误差。用来反向传播，更新权重。（error是一个矢量，长度为样本的数量，
            # 保存的是每一个样本的误差值。
            error = y - a
            self.w_ += self.alpha * X.T.dot(error)
            self.b_ += self.alpha * error.sum()
            # 计算损失值。
            cost = (error ** 2).sum() / 2.0
            # 加入损失列表中
            self.cost_.append(cost)
    
    def activation(self, X):
        """激活函数。这里使用y=x作为激活函数。
        
        Parameters
        ------
        X : 数组类型
            净输入
        
        Returns
        -----
        r : 数组类型
            激活之后的结果。
        """
        return X
        
    def predict(self, X):
        """进行预测。
        Parameters
        -----
        X : 类数组类型。
            待预测的样本。
        """
        net_input = np.dot(X, self.w_) + self.b_
        return self.activation(net_input)
        

X, y = load_boston(return_X_y=True)
X

X, y = load_boston(return_X_y=True)
y = y.reshape(-1, 1)
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.25, random_state=0)
# 对特征列进行标准化处理。
s = StandardScaler()
train_X = s.fit_transform(train_X)
test_X = s.transform(test_X)
s2 = StandardScaler()
train_y = s2.fit_transform(train_y)
test_y = s2.transform(test_y)
ada = AdaLine(0.0005, 20)
ada.fit(train_X, train_y)
result = ada.predict(test_X)
display(result)
display(ada.cost_)
display(mean_squared_error(test_y, result))

import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"]=False

plt.figure(figsize=(10, 10))
# 绘制预测值.
plt.plot(result, "ro-", label="预测值")
# 绘制真实值
plt.plot(test_y, "go--", label="真实值")
plt.title("自适应神经元-梯度下降")
plt.xlabel("样本序号")
plt.ylabel("房价")
plt.legend()
plt.show()

# 绘制累计误差值
plt.plot(range(1, ada.times + 1), ada.cost_, "o-")

# 因为房价分析涉及多个维度，不方便进行可视化，为了
# 实现可视化，我们只选取其中的一个维度（RM），并画出直线，
# 实现拟合。
X, y = load_boston(return_X_y=True)
X = X[:, 5]
X = X.reshape(-1, 1)
y = y.reshape(-1, 1)
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.25, random_state=0)
ada = AdaLine(alpha=0.0005, times=100)



# 对数据进行标准化处理。
s = StandardScaler()
train_X = s.fit_transform(train_X)
test_X = s.transform(test_X)
s2 = StandardScaler()
train_y = s2.fit_transform(train_y)
test_y = s2.transform(test_y)
ada.fit(train_X, train_y)
result = ada.predict(test_X)
display(mean_squared_error(test_y, result))

plt.scatter(train_X, train_y)
# 查看方程系数
display(ada.w_, ada.b_)
# 构建方程 y = w * x + b
x = np.arange(-5, 5, 0.1)
# y = 0.69822681 * x -1.5853984791647233e-15
plt.plot(x, y, "r")
# 也可以这样来做。
plt.plot(x, ada.predict(x.reshape(-1, 1)), "r")