暗通道去雾算法代码实现(1) python
文章目录
- 前言
- 一、腐蚀膨胀操作
- 二、何凯明去雾论文思想的简单描述
-
- 1.关于暗通道先验
- 2.暗通道先验的理论依据:
- 3、有雾图像的形成模型
- 4、传输率t的估计
- 5、大气光的估计
- 6、使用导向滤波对传输率t进行进一步改进
- 总结
-
- 1、argsort
- 2、np.where 用法
- 3、
前言
今天开始好好研究去雾算法
第一篇
一、腐蚀膨胀操作
一般来说腐蚀膨胀操作都是对二值化后的图像进行操作,
(图像变为了0或255中的其中一个,之后若是腐蚀操作,用全为1的卷积核与二值化图像进行与操作,若全为255,则显示为白色,否则显示为黑色。膨胀操作是只要卷积核与二值化后的图像与之后有一个为255,就显示白色)
但今天在看别人代码时,求取以像素X为中心的一个窗口的像素最小值时直接在原始像素上使用了腐蚀操作,
有点疑惑,便进行了验证。
腐蚀膨胀操作原理
自己通过代码证明,对于没有二值化的图像,当卷积核为3时。
dc1是原始像素
dark是经过卷积核为3的腐蚀操作得到的,可以看到确实是在3*3的区域中取最小值作为当前像素的值
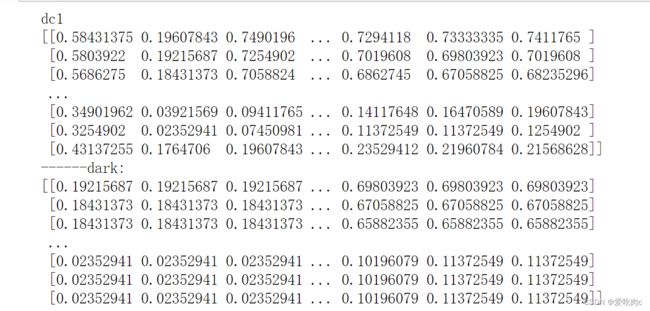
二、何凯明去雾论文思想的简单描述
1.关于暗通道先验
原文描述:
In most of the nonsky patches, at least one color channel has some pixels whose intensity are very low and close to zero. Equivalently, the minimum intensity in such a patch is close to zero.
在大多数非天空区域,至少有一个通道的像素值是很低的并且接近于0,并且在一个小的区域内最小的像素强度也接近于0.
暗通道先验的数学公式:
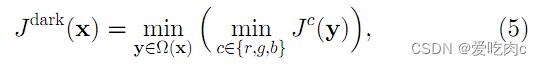
式中Jc表示彩色图像的每个通道 ,Ω(x)表示以像素X为中心的一个窗口。
式(5)的意义用代码表达也很简单,首先求出每个像素RGB分量中的最小值,之后利用opencv的腐蚀操作求出以每个像素为中心的一个窗口的最小值,一般有WindowSize = 2 * Radius + 1;
2.暗通道先验的理论依据:
原文:
The low intensity in the dark channel is mainly due to three factors: a) shadows, e.g., the shadows of cars, buildings, and the inside of windows in cityscape images, or the shadows of leaves, trees, and rocks in landscape images; b) colorful objects or surfaces, e.g., any object with low reflectance in any color channel (for example, green grass/tree/plant, red or yellow flower/leaf, and blue water surface) will result in low values in the dark channel; c) dark objects or surfaces, e.g., dark tree trunks and stones. As the natural outdoor images are usually colorful and full of shadows, the dark channels of these images are really dark!
这些低强度的像素值大多数是由于三个方面:a)现实中物体的阴影(其本身就有低的强度值) b)色彩鲜艳的物体或表面,在RGB的三个通道中有些通道的值很低(比如绿色的草地/树/植物,红色或黄色的花朵/叶子,或者蓝色的水面);c)颜色较暗的物体或者表面,例如灰暗色的树干和石头。总之,自然景物中到处都是阴影或者彩色,这些景物的图像的暗原色总是很灰暗的。
下面我进行了一些验证:对于无雾图 其暗通道:
import cv2
import numpy as np
img=cv2.imread("wu13.jpg")
b,g,r=cv2.split(img)
#三通道中像素最小值
min_data=cv2.min(cv2.min(r,g),b)
#获取卷积核
kernel=cv2.getStructuringElement(cv2.MORPH_RECT,(15,15))
#局部最小资
dark=cv2.erode(min_data,kernel)
cv2.imshow('dark',dark)
print(dark)
cv2.waitKey(0)
cv2.destroyAllWindows()
上述暗通道图像均使用的窗口大小为15*15,即最小值滤波的半径为7像素
3、有雾图像的形成模型
首先,在计算机视觉和计算机图形中,下述方程所描述的雾图形成模型被广泛使用:

![]()
其中I(x)是有雾(带去雾)图像,J(x)是无雾图像,tt是描述未散射并到达相机的那部分光的介质透射, A是全球大气光成分,
4、传输率t的估计
将式(1)稍作处理,变形为下式:
上标C表示R/G/B三个通道的意思。
首先假设在每一个窗口内透射率t(x)为常数,定义他为,并且A值已经给定,然后对式(7)两边求两次最小值运算,得到下式:
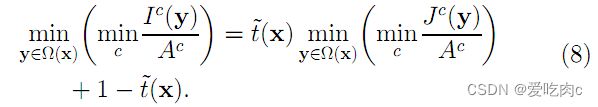
上式中,J是待求的无雾的图像,根据前述的暗原色先验理论有:
这就是透射率的预估值。公式右半部分两个最小值也可以通过暗通道定义的函数来计算
深度信息
实际上,即使在晴朗的日子里,大气也不是绝对没有任何粒子。所以当我们观察远处的物体时,雾霾仍然存在。此外,雾霾的存在是人类感知深度的基本线索 。这种现象称为空中透视。如果我们彻底消除雾霾,图像可能看起来不自然,我们可能会失去深度感。因此,有必要在去雾的时候保留一定程度的雾,这可以通过在式(11)中引入一个在[0,1] 之间的因子,则式(11)修正为:

本文中,w均取0.95 和论文中一致
def transestimate(img,A):
omega=0.95 #取值与论文中一致
ia=np.empty(img.shape,img.dtype)
for i in range(0,3):
ia[:,:,i]=img[:,:,i]/A[0,i] #每个通道单独计算
trans=1-omega*darkchannel(ia) #与论文中公式一致
trans = np.where(trans > 1, 1, trans)
trans = np.where(trans < 0, 0, trans)
return trans
5、大气光的估计
上文中都是假设大气光是已知的,现在我们需要来求取大气光的值,才能进一步求得无雾图像
直接选取I(X)中最亮的像素来作为大气光的估计是不准确的,
(这种只有在阴天或者太阳光可以被忽略的情况下才会成立),此时I(x)<=A
但大多数情况下,太阳光并不能被忽略(这就导致I(x)会大于A,如有雾图中的白色汽车,建筑等)。所以对于大气光的估计需要进一步改进。
何凯明教授采用的方法是:
具体步骤如下:
1) 从暗通道图中按照亮度的大小取前0.1%的像素。
2) 在这些位置中,在原始有雾图像I中寻找对应的具有最高亮度的点的值,作为A值。
在实际写代码中,采用的是这些像素的平均值作为大气光
这个代码是自己写的,在网上找了一些发现其实是错的,看了网上很多代码,结果求出的索引全为0,发现是argsort算法用错,具体见文章末尾总结
def AlightE(img,dark):
[h,w]=img.shape[:2]
imsize=h*w #像素个数
numpx=int(max(math.floor(imsize/1000),1))#选取前百分之0.1的像素个数,不能少于一个
# imvec=img.reshape(imsize,3) #图像向量
darkvec=dark.reshape(1,imsize) #按通道向量
b,g,r=cv2.split(img)
bvec=b.reshape(1,imsize)#将每个通道都变成1行imsize列,为了根据索引求和
gvec=g.reshape(1,imsize)
rvec=r.reshape(1,imsize)
index=darkvec.argsort() #暗通道向量值按照从小到大排,并返回索引
index=index[:,imsize-numpx::]#获取到前百分之零点一的像素在darkvex中的索引值
sumpx=np.zeros([1,3])
#下列是分别求取前百分之零点1的原图像素在各通道的像素值
for j in range(0,numpx):
sumpx[0,0]+=bvec[0,index[0,j]]
for j in range(0,numpx):
sumpx[0,1]+=gvec[0,index[0,j]]
for j in range(0,numpx):
sumpx[0,2]+=rvec[0,index[0,j]]
#把这些像素的平均值作为大气光
sumpx/=numpx
return sumpx
6、使用导向滤波对传输率t进行进一步改进
我们发现当假设局部传输率一致时,此时暗通道中会出现光晕体和块,这是由于局部内的传输率t并不一定是相同的。
本文使用导向滤波对传输率t进行进一步优化
见下篇啦
今天好累~~明天再继续
总结
1、argsort
对于一行n列和n行1列 会出差错 小心
这里是1行n列 没错
a=np.array([[233,200,100]])
a.argsort()
结果:
array([[2, 1, 0]], dtype=int64)
这里是n行1列就有错了
在这里插入代码片a=np.array([[233],[200],[100]])
a.argsort()
结果:
array([[0],
[0],
[0]], dtype=int64
n行n列
a=np.array([[233,100],[200,1],[100,0]])
a.argsort()
结果:
array([[1, 0],
[1, 0],
[1, 0]], dtype=int64)
可以看出对于argsort()是每行每行比较并返回相应索引的
2、np.where 用法
第一种用法 np.where(condition)返回结果为元组
①返回一个元组,每个元素都是array类型,先返回二维数组中所在位置,再返回相对应一维数组位置
a=np.array([[2,3,1,8,6,4],[4,5,6,7,8,3]])
np.where(a<4)
结果:
(array([0, 0, 0, 1], dtype=int64), array([0, 1, 2, 5], dtype=int64))
a=np.array([
[
[2,3,1,8,6,4],
[4,5,6,7,8,3]
],
[
[2,3,1,8,6,4],
[4,5,6,7,8,3]
]
])
np.where(a<4)
结果:
(array([0, 0, 0, 0, 1, 1, 1, 1], dtype=int64),
array([0, 0, 0, 1, 0, 0, 0, 1], dtype=int64),
array([0, 1, 2, 5, 0, 1, 2, 5], dtype=int64))
②也可以得到其中的元素通过索引获得,此时得到的就是array数组
a=np.array(
[
[2,3,1,8,6,4],
[4,5,6,7,8,3]
])
np.where(a<4)[0]
结果:array([0, 0, 0, 1], dtype=int64)
(在二维数组中的位置,行)
若为np.where[1]
结果:array([0, 1, 2, 5], dtype=int64)
(列)
第二种用法 np.where(condition,x,y) 返回结果仍为array
若满足条件 则变为a,否则为b
a=np.array(
[
[2,3,1,8,6,4],
[4,5,6,7,8,3]
])
np.where(a<4,0,a)
结果:
array([[0, 0, 0, 8, 6, 4],
[4, 5, 6, 7, 8, 0]])
3、
今天自己发现了网上很多 求大气光代码都是错的 自己更正了!!好开心好开心,要继续加油哦