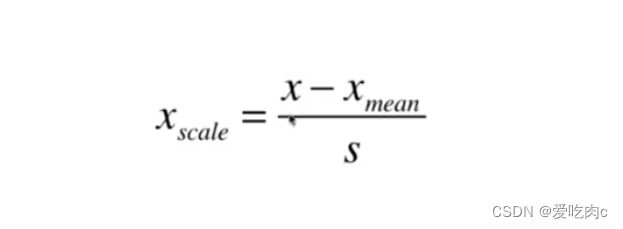机器学习 之数据归一化

---

一、为什么要进行数据归一化

比如 样本特征中
在这里，虽然肿瘤大小样本2是样本1的五倍，发现时间样本2仅是样本1的两倍，但是该数据仍主要有发现天数所主导，是因为两个特征的量纲并不相同。
若修改量纲，将发现时间的单位修改成年，则又会被肿瘤大小所主导

我们可以发现，若不进行数据归一化，则不能很好的反映每一个特征它的重要程度

二、解决方法：将所有数据映射到同一个尺度

1.最值归一化 normalization

这种适用于：
有明显边界的情况，比如学生成绩，最低可能为0，最高为100。又比如图像的像素。
**缺点：**受outlier影响较大，比如很多人的收入在1万元左右，而有一个人的收入是100万元，此时受边界值影响就会很大，会导致很多值在均值归一化之后都在0附近。

2.均值方差归一化 standardization

把所有数据都归一到均值为0方差为1的分布中，并不保证归一化后的值在0-1之间。
适用于没有明显边界的特征值，有可能存在极端数据值的样本中。
但是 这里推荐，如果不像上述所描述的如图像像素等有明显的边界值，都可以使用均值方差归一化。

1、公式

2、公式说明:

在这里 x是每一个特征值组成的向量，xmean是对应的平均值。 S是标准差
首先减去均值就相当于把数据分布进行平移，即改变平均值。使数据的平均值都为0。这样并不会改变数据分布中各个点之间的距离。然后因为标准差可以理解为平均每个点距离平均值的距离，除以标准差就相当于以前平均每个点距离0的距离为S，现在变成了1。这样的话，对于数据中每个点的所有特征维度距离0的量纲就保持一致了。最后数据就都为均值为0，方差为1的正态分布了。

三、 示例：

1、最值归一化

import numpy as np

x=np.random.randint(0,100,size=100)  #0-100的整数 100个数
x=(x-np.min(x))/(np.max(x)-np.min(x))
x

2、均值方差归一化

import numpy as np
import matplotlib.pyplot as plt
x=np.random.randint(0,100,(20,2))
x=np.array(x,dtype=float)  #进行均值方差归一化 会产生浮点数 所以要转换为浮点类型
x[:,0]=(x[:,0]-np.mean(x[:,0]))/np.std(x[:,0]) #第一个特征
x[:,1]=(x[:,1]-np.mean(x[:,1]))/np.std(x[:,1]) #第二个特征
plt.scatter(x[:,0],x[:,1])
plt.show()

四、在机器学习中如何对测试数据集进行归一化？

1、方法：

首先我们要求出训练数据集中的平均值与方差，但是对于测试数据集，我们可能只有一个数据，是没有办法求均值与方差的，所以对于测试数据集进行归一化大方法应该是：



使用scikit-learn中的 Scaler对训练数据集进行fit操作 即可得到并保存训练数据集的标准差和平均值，之后通过transform 即可对输入样例根据该训练数据集进行归一化操作。

2、使用scikit-learn中的StandardScaler类

来进行数据集的均值方差归一化操作

1、代码：（这里使用的是鸢尾花数据）

from sklearn.model_selection import train_test_split  #将数据分为数据集和训练集
import numpy as np
from sklearn import datasets
iris=datasets.load_iris()
X=iris.data
Y=iris.target
#测试数据集的比例0.2
x_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target,test_size=0.2,random_state=666)#这里设置了一个随机种子
from sklearn.preprocessing import StandardScaler
standardScaler=StandardScaler()#实例化一个对象
standardScaler.fit(x_train)
standardScaler.mean_
standardScaler.scale_   #std_已经不再使用了，开始使用scale 方差也就是一个分布范围
x_train=standardScaler.transform(x_train)  #分别进行归一化
x_test=standardScaler.transform(x_test)

from sklearn.neighbors import KNeighborsClassifier #k近邻算法
knn_classfier=KNeighborsClassifier(n_neighbors=3) #这里设n为3
knn_classfier.fit(x_train,y_train)
knn_classfier.predict(x_test)
knn_classfier.score(x_test,y_test)  #预测准确度 这里记得如果训练数据集进行了归一化操作，则测试数据也要归一化

2、scikit-learn中的StandardScaler类

1、有一个初始化操作，设mean和scale 均为None
2、有一个fit函数，这个函数的目的是根据传进来的训练数据集 计算出相对应的方差和均值，返回的结果仍是一个StandardScaler类
3、有一个transform函数，这个函数是对传进来的数据根据训练数据集的方差和均值进行均值方差归一化。

简单实现 这里都是假设二维

import numpy as np

class StandardScaler:
    def __init__(self):
        self.std_=None
        self.scale_=None
    def fit(self,X):
        self.mean_=np.array([np.mean(X[:,i])for i in range(X.shape[1])])
        self.scale_ = np.array([np.std(X[:, i]) for i in range(X.shape[1])])
        return self
    def transform(self,X):
        resx=np.array(shape=X.shape,dtype=float) #将resx结果定为float类型
        for col in range(X.shape[1]):
            resx=(X[:,col]-self.mean_[col])/self.scale_[col]
        return resx