梯度下降法

---

一、什么是梯度下降法？

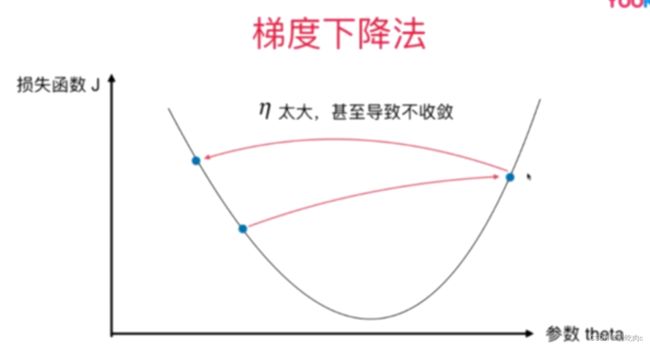
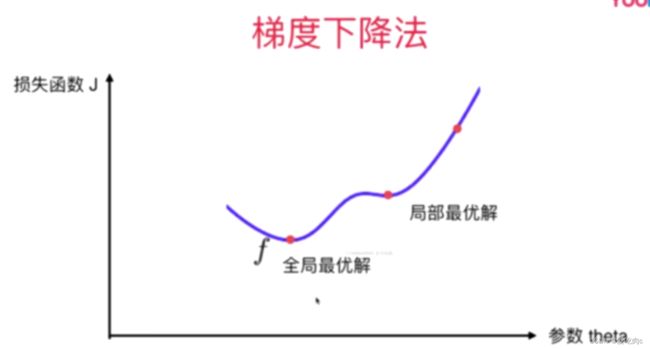
梯度法并不是一个机器学习算法，既不是监督学习，也不是非监督学习，是一种基于搜索的最优化方法

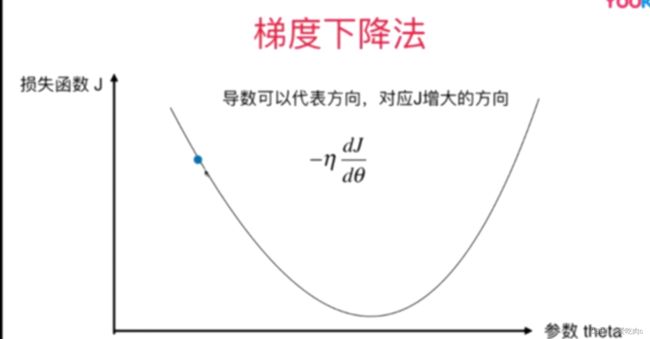
	梯度可以代表方向，对应损失函数增大的方向，加上一个符号就代表J减小的方向。
	n成为学习率

并不是所有函数都有唯一的极值点

二、模拟梯度下降法

1.代码实现（这里使用了一个二次函数来模拟）

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-1, 6, 141)  
y = (x - 2.5) ** 2 - 1


# eta 学习率 epsilon:由于eta，梯度下降不一定会完全到达梯度为0的点，这里设置一个epsilon，当前一个损失函数的值与本次的值小于该epsilon时，就说明到达最低
# 因为随着梯度下降，损失函数的差值会越来越小（前提是eta学习率设置合理的情况下）
# 设置n_iters 即最大循环次数，因为eta是一个超参数，若eta设置不合理
# 可能会出现损失函数越来越大的情况，此时是死循环
def gradient_descent(initial_x, eta, n_iters=1e3, epsilon=1e-8):
    theta = initial_x
    theta_history.append(initial_x)
    i_iters = 0
    while i_iters < n_iters:
        last_theta = theta  # 保存上次theta
        gradient = DJ(theta)
        theta = theta - eta * gradient
        theta_history.append(theta)
        if (np.abs(J(theta) - J(last_theta)) < epsilon):
            break
        i_iters += 1
#求梯度

def DJ(x):
    return 2 * (x - 2.5)
#求损失函数

def J(x):
    return (x - 2.5) ** 2 - 1

#绘制梯度下降过程
def plot_theta_history():
    plt.plot(x, J(x))
    plt.plot(np.array(theta_history), J(np.array(theta_history)), color="r",marker='+')
    plt.show()


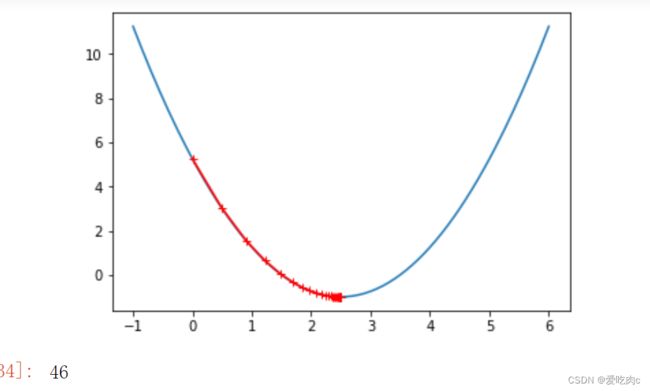
eta = 0.8  #梯度下降过程 不必都是从一侧下降的 只要损失函数的值在变小就可以

#theta_history 来保存梯度下降的过程中x的值
theta_history = []
gradient_descent(0, eta)
plot_theta_history()
len(theta_history)

若eta=0.1

eta=0.8

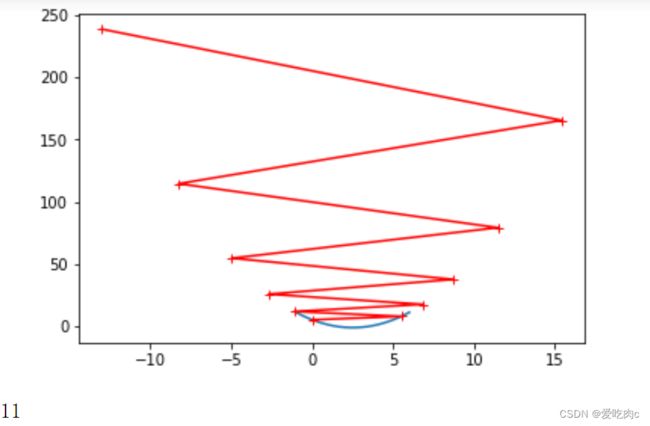
设置n_iters为10 即最大循环10次 eta=1.1 来看损失函数增大的情况，这种情况证明eta设置过大

三、线性回归中使用梯度下降算法

1、概述：

线性回归中theta最少都有两个值，所以在这里应该用梯度而不是导数

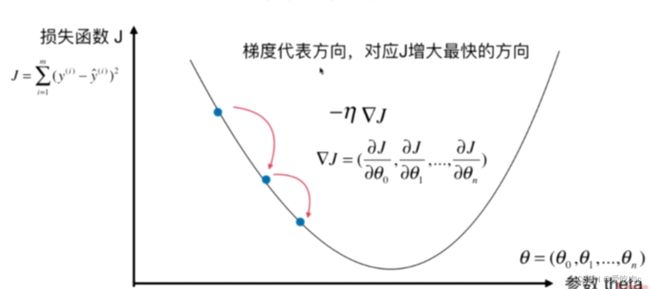
梯度是一个向量

我们注意到 如果对该损失函数对theta求偏导 会导致每个参数都与m有关，值会很大，为了使与m无关
我们修改损失函数
这里也让我们学到：我们设置的损失函数不一定是适合的，在实际过程中
我们应该动态调整损失函数
Xb*theta  即为预测值 Xb是在X矩阵的基础上 添加了一列1 可见上一篇

2、代码实现：

import matplotlib.pyplot as plt
import numpy as np
np.random.seed(666) #设置一个随机种子，以便让每次运行时结果都相同
x=np.random.random(size=100)
y=3.*x+4.+np.random.normal(size=100)
X=x.reshape(-1,1) #把x变成二维，以便之后拓展到有多个样本特征的数据
#求损失函数
def J(X_b,y,theta):
    try:
        return np.sum((y-X_b.dot(theta))**2)/len(X_b)
    except:
        return float('inf')  #防止eta不合理出错
#求梯度
def dJ(X_b,y,theta):
    res=np.empty(len(theta)) #梯度是一个向量  与theta系数的大小相同
    #res[0]单独求
    res[0]=np.sum(X_b.dot(theta)-y)
    for i in range(1,len(theta)):
        res[i]=np.sum((X_b.dot(theta)-y).dot(X_b[:,i]))
    res=res*2/len(X_b)
    return res
#梯度下降过程
def gradient_descent(X_b,y,initial_theta, eta, n_iters=1e3, epsilon=1e-8):
    theta = initial_theta
    i_iters = 0
    while i_iters < n_iters:
        last_theta = theta  # 保存上次theta
        gradient = dJ(X_b,y,theta)
        theta = theta - eta * gradient
        if (np.abs(J(X_b,y,theta) - J(X_b,y,last_theta)) < epsilon):
            break
        i_iters+=1
    return theta
#在原先系数的基础上加上一列1，即那个偏移量，为了与X1....Xn保持一致，1代表X0的系数为1
X_b=np.hstack([np.ones((len(X),1)),X])
eta=0.01
initial_theta=np.zeros(X_b.shape[1])
theta=gradient_descent(X_b,y,initial_theta,eta)
theta

\

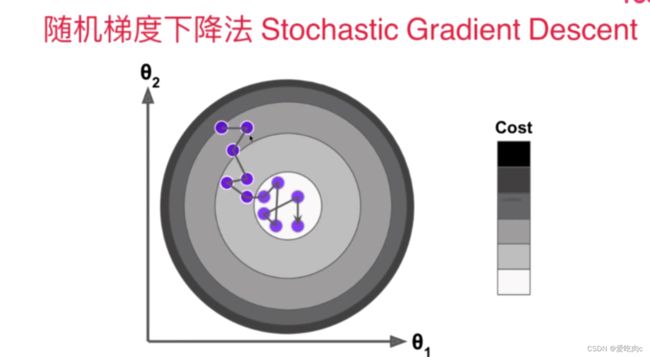
四、随机梯度下降法

1、批量梯度下降和随机梯度下降

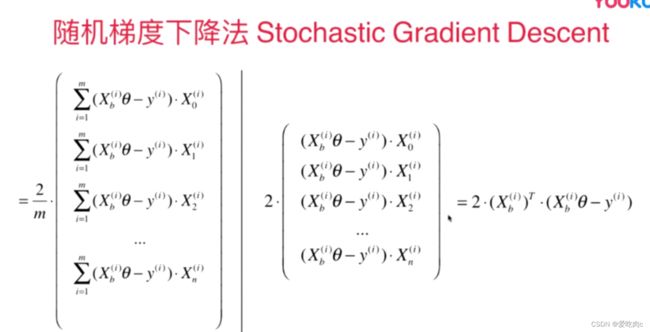
批量梯度下降法就是上述的方法，计算梯度中的每个偏导数都需要对所有样本进行计算
这样会导致当样本数量过多时，运行速度很慢
因此提出了随机梯度下降

随机梯度下降法中求得并不是真正的梯度，在批量梯度下降中，梯度是损失函数下降的方向，且是下降最快的方向
但是在随机梯度中这个方向并不保证损失函数一定在减少，也并不保证损失函数一定是朝着下降最快的方向。

如图：

即使随机梯度下降具有不可预测性，但是实验结果告诉我们，随机梯度下降最后依然能够差不多的到达损失函数最小的点。
即让模拟数据与真实数据较为接近。

注意：在随机梯度中，学习率并不能是一个固定值
在批量梯度下降中，学习率是一个固定值，这是因为只要学习率这个超参数取值合适，则损失函数总是朝着梯度下降最快的方向。但是在随机梯度中，因为方向具有不可预测性，即使已经到达了最小值附近，但是由于梯度是一个固定值，可能会导致跳出了该最小值

在随机梯度中，学习率应该是一个变化值，且要随着次数减小

在这里 a我们采用5 b我们采用50 i_iters 是我们循环的次数

2、代码实现随机梯度

import matplotlib.pyplot as plt
import numpy as np
np.random.seed(233) #设置一个随机种子，以便让每次运行时结果都相同
m=100000
x=np.random.random(size=m)
y=3.*x+4.+np.random.normal(0,3,size=m)
X=x.reshape(-1,1) #把x变成二维，以便之后拓展到有多个样本特征的数据
#求梯度  这里并非真正的梯度 这里只需传进一个样本即可
def dJ_sgd(X_b_i,y_i,theta):
    return X_b_i.T.dot(X_b_i.dot(theta)-y_i)*2

#梯度下降过程
def gsd(X_b,y,initial_theta,n_iters):
    theta = initial_theta
    i_iters = 0
    t1=5
    t2=50
    def learning_rate(t):
        return t1/(t+t2)
    for cur_iters in range(n_iters):
        rand_i=np.random.randint(len(X_b))
        gradient=dJ_sgd(X_b[rand_i],y[rand_i],theta)
        theta=theta-learning_rate(cur_iters)*gradient
    return theta
#在原先系数的基础上加上一列1，即那个偏移量，为了与X1....Xn保持一致，1代表X0的系数为1
X_b=np.hstack([np.ones((len(X),1)),X])
initial_theta=np.zeros(X_b.shape[1])
theta=gsd(X_b,y,initial_theta,n_iters=len(X_b//3))
theta

%%time
#在原先系数的基础上加上一列1，即那个偏移量，为了与X1....Xn保持一致，1代表X0的系数为1
X_b=np.hstack([np.ones((len(X),1)),X])
initial_theta=np.zeros(X_b.shape[1])
theta=gsd(X_b,y,initial_theta,n_iters=len(X_b//3)) #只循环了样本个数的三分之一次
theta

结果：
array([3.9809955 , 2.99786789])

时间：
Wall time: 736 ms

而批量梯度下降的时间：
Wall time: 1.16 s

	我们可以发现运用随机梯度下降，我们也可以取得较好的结果 参数接近我们设置的二次函数4和3
	并且随机梯度下降总共的循环过程还不及批量梯度下降求梯度中一个值的次数多。

3、优化

	上述随机梯度的实现不够好，因为我们只是对我们所有样本中的三分之一考虑了进来
	但在实际过程中，我们至少应该把所有样本都考虑进来
	这里的n_iters 代表的是我们把样本数据看几圈 至少一遍

import matplotlib.pyplot as plt
import numpy as np
np.random.seed(233) #设置一个随机种子，以便让每次运行时结果都相同
m=100000
x=np.random.random(size=m)
y=3.*x+4.+np.random.normal(0,3,size=m)
X=x.reshape(-1,1) #把x变成二维，以便之后拓展到有多个样本特征的数据
#求梯度  这里并非真正的梯度 这里只需传进一个样本即可
def dJ_sgd(X_b_i,y_i,theta):
    return X_b_i.T.dot(X_b_i.dot(theta)-y_i)*2

#梯度下降过程
def gsd(X_b,y,initial_theta,n_iters=3):
    theta = initial_theta
    i_iters = 0
    t1=5
    t2=50
    def learning_rate(t):
        return t1/(t+t2)
    m=len(X_b)
    for cur_iters in range(n_iters):  #第几圈
        indexs=np.random.permutation(m)  #因为我们的方向是随机的 所以在这里对样本进行了乱序处理
        #如果还是向上面那样使用randint 并不能保证在我们循环的几圈中能考虑进来所有样本
        #对其进行乱序，可以使我们每一圈都能顾及到所有样本
        X_b_new=X_b[indexs]
        y_new=y[indexs]
        for i in range(m):
            gradient=dJ_sgd(X_b_new[i],y_new[i],theta)
            theta=theta-learning_rate(cur_iters*m+i)*gradient   #这里循环次数的计算方法也有所改变
    return theta

4、sklearn中的随机梯度下降 （这里使用波士顿这个真实数据）

记得数据归一化 这里用均值方差归一化的方法

from sklearn.linear_model import SGDRegressor #这里随机梯度只能解决线性模型
from sklearn import datasets
from sklearn.model_selection import train_test_split
boston=datasets.load_boston()
x=boston.data #只用平均房间数这一个样本特征
y=boston.target
x=x[y<50]
y=y[y<50]
x_train,x_test,y_train,y_test=train_test_split(x,y)

#归一化
from sklearn.preprocessing import StandardScaler
stdsc=StandardScaler()
stdsc.fit(x_train)  #求出 mean 与 std
x_train_standscaler=stdsc.transform(x_train)
x_test_standscaler=stdsc.transform(x_test)

sgd_reg=SGDRegressor(n_iter=100)
%time sgd_reg.fit(x_train_standscaler,y_train)
sgd_reg.score(x_test_standscaler,y_test)

五、如何计算梯度计算的准确 性

在机器学习中，我们是根据损失函数来计算梯度
根据损失函数求导计算所得。
那我们如何计算我们计算梯度的准确性呢？
在这里我们可以根据高数中导数的计算来调试梯度。但是这个计算量比直接通过损失函数计算梯度复杂

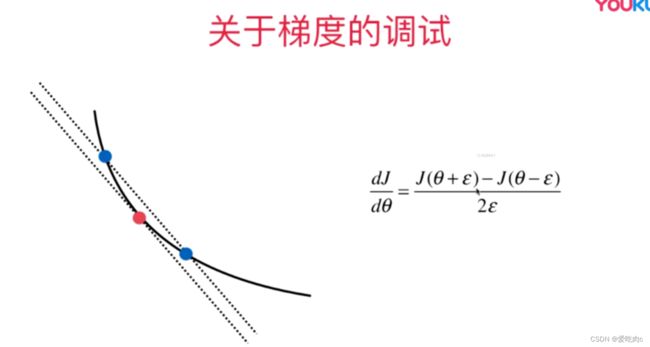
如在二维中，我们可以根据损失函数来计算出红色点的梯度。与此同时我们可以根据右侧的式子来调试梯度。
以此来判断我们通过公式计算出的梯度是否正确。拓展到多维：

损失函数的梯度，损失函数是为了让预测值与真实值接近，梯度预测的准确，则损失函数会更小，会更接近真实值。theta会越准确

import numpy as np

np.random.seed(666)
x=np.random.random(size=(1000,10))
true_theta=np.arange(1,12,dtype=float)
x_b=np.hstack([np.ones((len(x),1)),x])
y=x_b.dot(true_theta)+np.random.normal(size=1000)
#求损失函数
def J(X_b,y,theta):
    try:
        return np.sum((y-X_b.dot(theta))**2)/len(X_b)
    except:
        return float('inf')  #防止eta不合理出错
#求梯度
def dJ_math(X_b,y,theta):

    return X_b.T.dot(X_b.dot(theta)-y)*2./len(X_b)
def dJ_debug(X_b,y,theta,epsilon=0.01):
    res=np.empty(len(theta))
    for i in range(len(theta)):
        theta_1=theta.copy()
        theta_1[i]+=epsilon
        theta_2=theta.copy()
        theta_2[i]-=epsilon
        res[i]=(J(X_b,y,theta_1)-J(X_b,y,theta_2))/(2*epsilon)
    return res
#梯度下降过程
def gradient_descent(dJ,X_b,y,initial_theta, eta, n_iters=1e3, epsilon=1e-8):
    theta = initial_theta
    i_iters = 0
    while i_iters < n_iters:
        last_theta = theta  # 保存上次theta
        gradient = dJ(X_b,y,theta)
        theta = theta - eta * gradient
        if (np.abs(J(X_b,y,theta) - J(X_b,y,last_theta)) < epsilon):
            break
        i_iters+=1
    return theta

#在原先系数的基础上加上一列1，即那个偏移量，为了与X1....Xn保持一致，1代表X0的系数为1
X_b=np.hstack([np.ones((len(x),1)),x])
eta=0.01
initial_theta=np.zeros(X_b.shape[1])
theta=gradient_descent(dJ_debug,X_b,y,initial_theta,eta)
theta

六、有关梯度下降的更多深入讨论

1、分类

2、随机

机器学习本来就是不确定的，因此随机这个方法极其重要

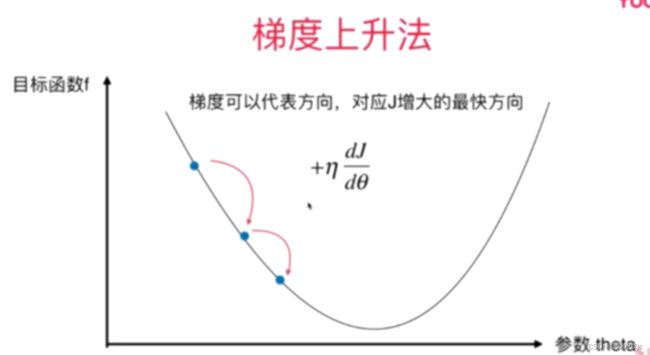
3、梯度上升法

4、总结

梯度法不是一个机器学习算法，而是基于搜索的最优化方法，如本章中将梯度下降运用在线性回归中
求损失函数的最小值，以便求得最合适的theta，但梯度法并非只能运用在线性中
下章将x学习PCA,我们一起加油!!!