python R 空间自回归模型SAR 参数估计 统计模拟 实验
一、编写一次估计函数
1. 载入numpy、固定随机种子
import numpy as np
np.random.seed(1)
2. 编写makeY函数,生成用于模拟实验的Y
def makeY(rho, sigma2true, Ysize):
I = np.identity(Ysize)
W = I/rho
# 使用while语句,必须保证I - rho * W可逆
while np.linalg.det(I - rho * W) == 0:
# 生成一列epsilon
epsilon = np.random.normal(0, sigma2true, Ysize)
# 生成邻接矩阵
A = I
for i in range(0 , Ysize) :
for j in range(0 , Ysize) :
if i < j:
A[i, j] = np.random.binomial(1, rho)
A[j, i] = A[i, j]
# 标准化带权邻接矩阵A,得到W
W = A/sum(A)
# 求所生成网络的密度,衡量其稀疏性
Ydensity = sum(sum(A)) / (Ysize * (Ysize - 1))
# 利用输入参数和随机数生成样本Y
Y = np.matmul(np.linalg.inv(I - rho * W), epsilon)
return [Y, W, Ydensity]
3. 编写主函数SAR_MLE_newton
def SAR_MLE_newton (rho, sigma2true, Ysize):
for i in range(1,1000):
Y = makeY(rho, sigma2true, Ysize)[0]
W = makeY(rho, sigma2true, Ysize)[1]
Ydensity = makeY(rho, sigma2true, Ysize)[2]
I = np.identity(Ysize)
# 使用牛顿迭代法估计对Y建立SAR模型后的参数
rhohatm = 0
dist1 = 0.01
Wf = I - (rhohatm * W)
np.linalg.det(Wf)
while abs(dist1)>1.0E-6:
Wf = I - (rhohatm * W)
rhohatm = rhohatm - dist1
if np.linalg.det(Wf) ==0:
break
else:
Ws = np.matmul(W, np.linalg.inv(Wf))
sigma2 = np.matmul(np.matmul(np.matmul(Y.T, Wf.T), Wf ), Y) / Ysize
a1rhohat = -np.trace(Ws) + np.matmul(np.matmul(np.matmul(Y.T, W.T), Wf), Y) / sigma2
a2rhohat = -np.trace(np.matmul(Ws, Ws)) - np.matmul(np.matmul(np.matmul(Y.T, W.T), W), Y) /sigma2
dist1 = a1rhohat / a2rhohat
if abs(dist1)<1.0E-6:
break
# 估计SE(σ)
a2rho = np.trace(np.matmul(Ws, Ws)) + np.trace(np.matmul(Ws.T, Ws))
a2sigma = Ysize / (2 * sigma2 * sigma2)
a2sigrho = np.trace(Ws) / sigma2
im = np.array([[a2sigma, a2sigrho], [a2sigrho, a2rho]])
sdhatm = np.sqrt(np.linalg.inv(im)[1, 1])
# 返回ρ的真实值、ρ的估计值、σ平方的真实值、σ平方的估计值
return [rho, rhohatm, sigma2true, sigma2, sdhatm, Ydensity]
二、选取不同的ρ、σ、Ysize,进行比较。
1. 生成待循环值
different_rho = np.arange(0.1, 1, 0.1)
different_sigma2 = np.arange(1, 20, 2)
different_Ysize = np.arange(10, 110, 10)
2. 初始化结果输出数组
result = np.zeros((different_rho.size, different_sigma2.size, different_sigma2.size, 6))
3. 多重循环,记录结果
for ii in range(0, different_rho.size):
for jj in range(0, different_sigma2.size):
for kk in range(0, different_Ysize.size):
result[ii, jj, kk, : ] = SAR_MLE_newton(different_rho[ii], different_sigma2[jj], different_Ysize[kk])
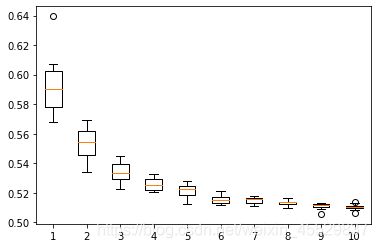
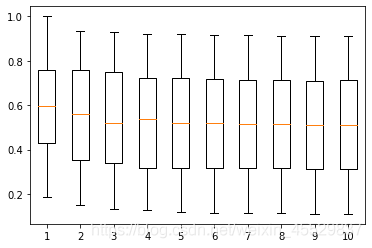
4 .绘制描述标准误分布的盒图,寻找规律
result1 = result[0,:,:,5]
result2 = result[:,0,:,5]
result3 = result[:,:,0,5]
for ii in range(1, different_rho.size):
result1 = result1 + result[ii,:,:,5]
for jj in range(0, different_sigma2.size):
result2 = result2 + result[:,jj,:,5]
for kk in range(0, different_Ysize.size):
result3 = result3 + result[:,:,kk,5]
import matplotlib.pyplot as plt
plt.boxplot(result1/different_rho.size)
plt.boxplot(result1.T/different_rho.size)
plt.boxplot(result2/different_sigma2.size)
plt.boxplot(result2.T/different_sigma2.size)
plt.boxplot(result3/different_Ysize.size)
plt.boxplot(result3.T/different_Ysize.size)
随着ρ的增大,预测标准误的均值会增大;
随着样本网络大小Y.size的增大,预测标准误会的均值和方差都会减少;
随着σ平方的增大,预测标准误差没有显著性差异。
附R代码(R的运算慢,写完后发现跑不起,所以换成了Python)
simulate_SAR_MLE_newtown <- function(rho, sigma2true, Ysize){
# 第一步:生成Y
I <- diag(1, Ysize)
# 生成一列epsilon
epsilon <- rnorm(Ysize, 0, sigma2true)
# 生成邻接矩阵
A <- I
for (i in 1 : Ysize){
for (j in 1 : Ysize){
if (i < j){
A[i, j] <- rbinom(1, 1, rho)
A[j, i] <- A[i, j]
}
}
}
# 求所生成网络的密度,衡量其稀疏性
Ydensity <- sum(A) / (Ysize * (Ysize - 1))
# 标准化带权邻接矩阵A,得到W
W <- t(t(A)/colSums(A))
# 利用输入参数和随机数生成样本Y
Y <- solve(I - rho * W) %*% epsilon
# 使用牛顿迭代法估计对Y建立SAR模型后的参数
rhohatm <- 0
dist1 <- 0.01
I <- diag(1, Ysize)
while(abs(dist1)>1.0E-6){
rhohatm <- as.numeric(rhohatm - dist1)
Wf <- I - (rhohatm * W)
Ws <- W %*% solve(Wf)
sigma2 <- t(Y) %*% t(Wf) %*% Wf %*% Y / Ysize
a1rhohat <- -sum(diag(Ws)) + t(Y) %*% t(W) %*% Wf %*% Y / sigma2
a2rhohat <- -sum(diag(Ws ^ 2)) - sigma2 ^ (-1) %*% t(Y) %*% t(W) %*% W %*% Y
dist1 <- a1rhohat / a2rhohat
}
a2rho <- sum(diag(Ws ^ 2)) + sum(diag(t(Ws) %*% Ws))
a2sigma <- Ysize / (2 * sigma2 ^ 2)
a2sigrho <- sum(diag(Ws)) / sigma2
im <- matrix(c(a2sigma, a2sigrho, a2sigrho, a2rho), 2, 2)
sdhatm <- sqrt(solve(im)[2, 2])
return(list(rhotrue = rho, rhohatm = rhohatm, sigma2true = sigma2true, sigma2hat = sigma2,sdhatm = sdhatm))
}