目标检测---CIOU原理及代码实现

目标检测—CIOU原理及代码实现

最近刚写完一篇YOLO V4-tiny的blog，其中Tensorflow2.0—YOLO V4-tiny网络原理及代码解析（三）- 损失函数的构建涉及到了CIOU。所以特地单独领出来写一篇blog记录一下。

在YOLO V3中，对于位置的损失函数，使用的还是普通的smooth-l1损失函数，但是到了YOLO V4中，关于位置的损失函数已经变成CIOU了。

一、原理，公式

关于它的原理，在YOLOV4与YOLOV3的区别中已经有了大致的介绍。

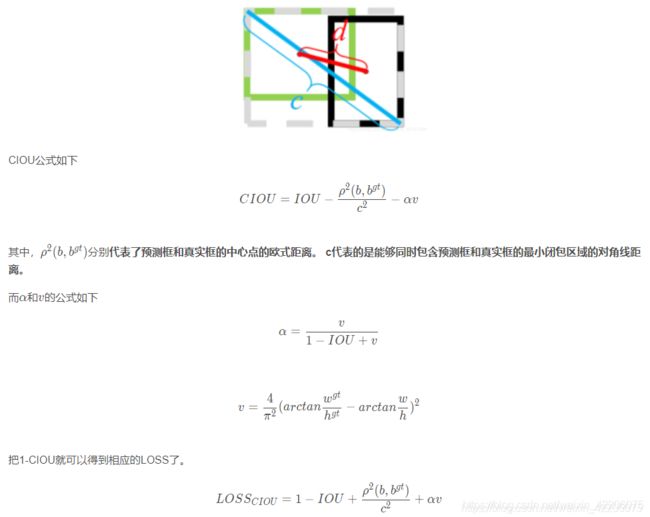
二、优点

相比于IOU的优点：
1.IOU没有考虑到两个框之间的位置信息，如果两个框没有重叠，它的IOU=0，没法进行反向传播。
2.还有一点，就是为什么之前的所有目标检测的网络中没有用iou直接作为损失函数。就是因为对于大小不同的框，iou值相同，但是其重叠程度却不同（说白了，就是对尺度不敏感）。在ciou中，由于有v这个概念，所以就使这种情况不可能再出现（个人理解，不对还请指正）。

三、代码实现

先来看下输入参数：

def box_ciou(b1, b2):
'''输入为：
    b1: tensor, shape=(batch, feat_w, feat_h, anchor_num, 4), xywh
    b2: tensor, shape=(batch, feat_w, feat_h, anchor_num, 4), xywh
'''

这里，我就用yolo系列的一个yolo head为例：b1和b2的shape=（2,13,13,3,4），其中4表示的是xywh。
第一步：先将输入的进行转换，转化为xyxy格式，其中b1_mins，b1_maxes ，b2_mins ，b2_maxes 的shape=（2,13,13,3,2）

	#   求出预测框左上角右下角
    b1_xy = b1[..., :2]
    b1_wh = b1[..., 2:4]
    b1_wh_half = b1_wh/2.
    b1_mins = b1_xy - b1_wh_half
    b1_maxes = b1_xy + b1_wh_half

    #   求出真实框左上角右下角
    b2_xy = b2[..., :2]
    b2_wh = b2[..., 2:4]
    b2_wh_half = b2_wh/2.
    b2_mins = b2_xy - b2_wh_half
    b2_maxes = b2_xy + b2_wh_half

第二步：计算真实与预测的iou值

	intersect_mins = K.maximum(b1_mins, b2_mins)
    intersect_maxes = K.minimum(b1_maxes, b2_maxes)
    intersect_wh = K.maximum(intersect_maxes - intersect_mins, 0.)
    intersect_area = intersect_wh[..., 0] * intersect_wh[..., 1]
    b1_area = b1_wh[..., 0] * b1_wh[..., 1]
    b2_area = b2_wh[..., 0] * b2_wh[..., 1]
    union_area = b1_area + b2_area - intersect_area
    iou = intersect_area / K.maximum(union_area,K.epsilon())

第三步：计算两个框的中心点的距离（ρ）

    center_distance = K.sum(K.square(b1_xy - b2_xy), axis=-1)

第四步：计算两个框的最小闭包区域的对角线大小（c）

	enclose_mins = K.minimum(b1_mins, b2_mins)
    enclose_maxes = K.maximum(b1_maxes, b2_maxes)
    enclose_wh = K.maximum(enclose_maxes - enclose_mins, 0.0)
    enclose_diagonal = K.sum(K.square(enclose_wh), axis=-1)

第五步：计算α

    ciou = iou - 1.0 * (center_distance) / K.maximum(enclose_diagonal ,K.epsilon())
    v = 4*K.square(tf.math.atan2(b1_wh[..., 0], K.maximum(b1_wh[..., 1],K.epsilon())) - tf.math.atan2(b2_wh[..., 0], K.maximum(b2_wh[..., 1],K.epsilon()))) / (math.pi * math.pi)
    alpha = v /  K.maximum((1.0 - iou + v), K.epsilon())

值得注意的是，v和alpha的shape都是为（2,13,13,3）

第六步：计算最终的ciou，并在最后一维增加一个维度

	ciou = ciou - alpha * v
    ciou = K.expand_dims(ciou, -1)

最终，输出的ciou的shape为（2,13,13,3,1）。

---

完整代码如下：

import math

import tensorflow as tf
from tensorflow.keras import backend as K
from tensorflow.keras import Input


def box_ciou(b1, b2):
    """
    输入为：
    ----------
    b1: tensor, shape=(batch, feat_w, feat_h, anchor_num, 4), xywh
    b2: tensor, shape=(batch, feat_w, feat_h, anchor_num, 4), xywh
    返回为：
    -------
    ciou: tensor, shape=(batch, feat_w, feat_h, anchor_num, 1)
    """
    #-----------------------------------------------------------#
    #   求出预测框左上角右下角
    #   b1_mins     (batch, feat_w, feat_h, anchor_num, 2)
    #   b1_maxes    (batch, feat_w, feat_h, anchor_num, 2)
    #-----------------------------------------------------------#
    b1_xy = b1[..., :2]
    b1_wh = b1[..., 2:4]
    b1_wh_half = b1_wh/2.
    b1_mins = b1_xy - b1_wh_half
    b1_maxes = b1_xy + b1_wh_half
    #-----------------------------------------------------------#
    #   求出真实框左上角右下角
    #   b2_mins     (batch, feat_w, feat_h, anchor_num, 2)
    #   b2_maxes    (batch, feat_w, feat_h, anchor_num, 2)
    #-----------------------------------------------------------#
    b2_xy = b2[..., :2]
    b2_wh = b2[..., 2:4]
    b2_wh_half = b2_wh/2.
    b2_mins = b2_xy - b2_wh_half
    b2_maxes = b2_xy + b2_wh_half

    #-----------------------------------------------------------#
    #   求真实框和预测框所有的iou
    #   iou         (batch, feat_w, feat_h, anchor_num)
    #-----------------------------------------------------------#
    intersect_mins = K.maximum(b1_mins, b2_mins)
    intersect_maxes = K.minimum(b1_maxes, b2_maxes)
    intersect_wh = K.maximum(intersect_maxes - intersect_mins, 0.)
    intersect_area = intersect_wh[..., 0] * intersect_wh[..., 1]
    b1_area = b1_wh[..., 0] * b1_wh[..., 1]
    b2_area = b2_wh[..., 0] * b2_wh[..., 1]
    union_area = b1_area + b2_area - intersect_area
    iou = intersect_area / K.maximum(union_area,K.epsilon())

    #-----------------------------------------------------------#
    #   计算中心的差距
    #   center_distance (batch, feat_w, feat_h, anchor_num)
    #-----------------------------------------------------------#
    center_distance = K.sum(K.square(b1_xy - b2_xy), axis=-1)
    enclose_mins = K.minimum(b1_mins, b2_mins)
    enclose_maxes = K.maximum(b1_maxes, b2_maxes)
    enclose_wh = K.maximum(enclose_maxes - enclose_mins, 0.0)
    #-----------------------------------------------------------#
    #   计算对角线距离
    #   enclose_diagonal (batch, feat_w, feat_h, anchor_num)
    #-----------------------------------------------------------#
    enclose_diagonal = K.sum(K.square(enclose_wh), axis=-1)
    ciou = iou - 1.0 * (center_distance) / K.maximum(enclose_diagonal ,K.epsilon())
    
    v = 4*K.square(tf.math.atan2(b1_wh[..., 0], K.maximum(b1_wh[..., 1],K.epsilon())) - tf.math.atan2(b2_wh[..., 0], K.maximum(b2_wh[..., 1],K.epsilon()))) / (math.pi * math.pi)
    alpha = v /  K.maximum((1.0 - iou + v), K.epsilon())
    ciou = ciou - alpha * v

    ciou = K.expand_dims(ciou, -1)
    return ciou

if __name__ == '__main__':
    b1 = Input(shape=(13,13,3,4))
    b2 = Input(shape=(13,13,3,4))
    ciou = box_ciou(b1,b2)

代码转载于： https://blog.csdn.net/weixin_44791964/article/details/107302710?spm=1001.2014.3001.5501