【数字图像处理】第6章 图像的锐化处理
6 图像的锐化处理
目录
-
- (一)图像锐化的概念
- (二)图像锐化的方法
-
-
- 1)一阶微分锐化
-
- ① 单方向的一阶锐化
- ② 无方向一阶锐化
- 2)二阶微分锐化
- 3)一阶与二阶微分的边缘提取效果比较
-
(一)图像锐化的概念
图像锐化的概念
图像锐化的目的是加强图像中景物的细节边缘和轮廓。
锐化的作用是使灰度反差增强。
因为边缘和轮廓都位于灰度突变的地方。所以锐化算法的实现是基于微分作用。
(二)图像锐化的方法
1)一阶微分锐化
基本原理
对于一元函数 f ( t ) f(t) f(t),一阶微分算子可以定义如下: ▽ f ( t ) = f ( t + 1 ) − f ( t ) ▽ f(t)= f(t+1)- f(t) ▽f(t)=f(t+1)−f(t)
对于二元图像(函数) f ( x , y ) f(x,y) f(x,y),一阶微分的定义是通过梯度实现的。
梯度的定义
图像 f ( x , y ) f(x,y) f(x,y) 在其坐标 ( x , y ) (x,y) (x,y) 上的梯度是一个二维列向量:
▽ f ( x , y ) = b m a t r i x = [ G x G y ] = [ δ f δ x δ f δ y ] ▽ f(x,y)= {bmatrix}=\begin{bmatrix} Gx\\ Gy\end{bmatrix}=\begin{bmatrix} \frac{\delta f}{\delta x}\\ \frac{\delta f}{\delta y}\end{bmatrix} ▽f(x,y)=bmatrix=[GxGy]=[δxδfδyδf]
其中 ▽ f ▽ f ▽f 的大小为 f ( x , y ) f(x,y) f(x,y) 的最快变化率; ▽ f ▽ f ▽f 的方向为 f ( x , y ) f(x,y) f(x,y) 的最快变化方向
梯度的模
梯度的物理意义
梯度的物理意义:任一点(x,y)处一个边缘的方向与该点处的梯度向量的方向正交。
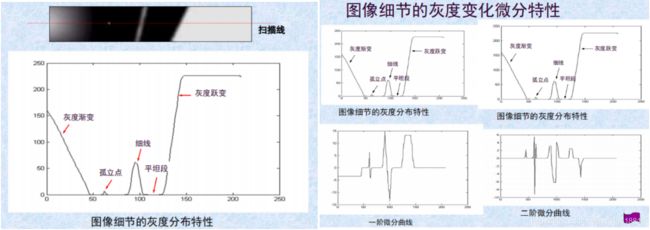
在灰度变化平缓的区域其梯度值较小,图像中灰度变化较大的边缘区域梯度值大,而在灰度均匀区域其梯度值为零。
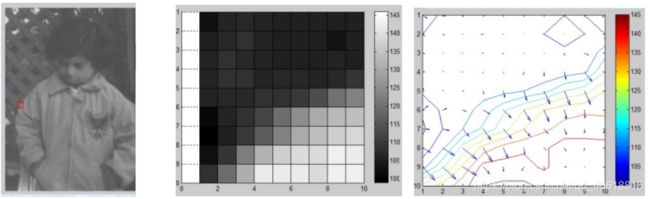
为了度量图像灰度的变化,需要建立一种向量与数量之间的映射关系。映射关系不同,则对应不同的一阶微分算子。
① 单方向的一阶锐化
基本原理
单方向的一阶锐化是指对某个特定方向上的边缘信息进行增强。
因为图像为水平、垂直两个方向组成,所以,所谓的单方向锐化实际上是包括水平方向与垂直方向上的锐化。
水平方向的一阶锐化
基本方法
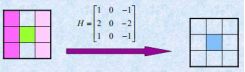
水平方向的锐化非常简单,通过一个可以检测出水平方向上的像素值的变化模板来实现。
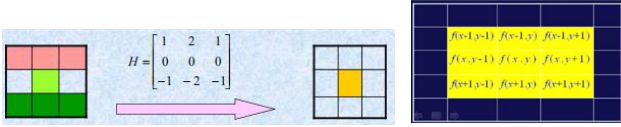
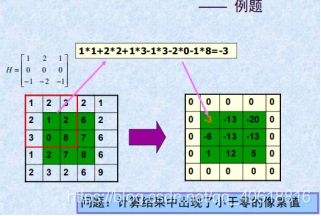
垂直方向的一阶锐化
基本方法
垂直锐化算法的设计思想与水平锐化算法相同,通过一个可以检测出垂直方向上的像素值的变化模板来实现。
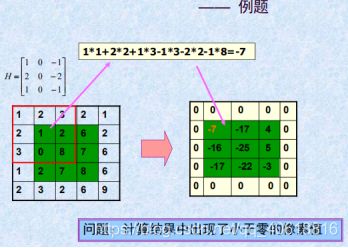
② 无方向一阶锐化
问题的提出
前面的锐化处理结果对于人工设计制造的具有矩形特征物体(例如:楼房、汉字等)的边缘的提取很有效。但是,对于不规则形状(如:人物)的边缘提取,则存在信息的缺损
设计思想
为了解决上面的问题,就希望提出对任何方向上的边缘信息均敏感的锐化算法。
因为这类锐化方法要求对边缘的方向没有选择,所有称为无方向的锐化算法。

几种方法的效果比较
Sobel算法与Priwitt算法的思路相同,属于同一类型,因此处理效果基本相同。
Roberts算法的模板为 2 ∗ 2 2*2 2∗2,提取出的信息较弱。
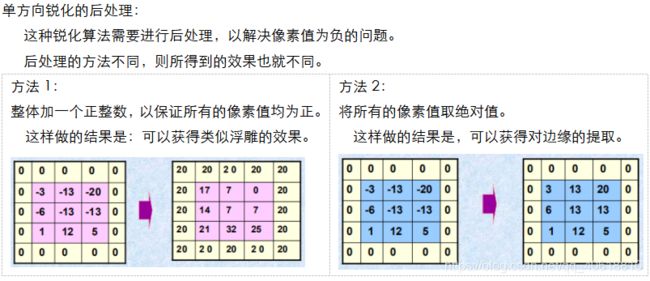
单方向锐化经过后处理之后,也可以对边界进行增强。
2)二阶微分锐化
问题的提出
从图像的景物细节的灰度分布特性可知,有些灰度变化特性一阶微分的描述不是很明确,为此,采用二阶微分能够更加获得更丰富的景物细节。
景物细节对应关系
1)对于突变形的细节,通过一阶微分的极大值点,二阶微分的过0点均可以检测出来。
2)对于细线形的细节,通过一阶微分的过0点,二阶微分的极小值点均可以检测出来。
3)对于渐变的细节,一般情况下很难检测,但二阶微分的信息比一阶微分的信息略多。
算法推导

Laplacian 算法
由前面的推导,写成模板系数形式形式即为Laplacian算子:
H 1 = [ 0 − 1 0 − 1 4 − 1 0 − 1 0 ] H_1=\begin{bmatrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0& -1 & 0 \\ \end{bmatrix} H1=⎣⎡0−10−14−10−10⎦⎤
Laplacian变形算法
为了改善锐化效果,可以脱离微分的计算原理,在原有的算子基础上,对模板系数进行改变,获得Laplacian变形算子如下所示。
H 2 = [ − 1 − 1 − 1 − 1 8 − 1 − 1 − 1 − 1 ] H 3 = [ 1 − 2 1 − 2 4 − 2 1 − 2 1 ] H 4 = [ 0 − 1 0 − 1 5 − 1 0 − 1 0 ] H_2=\begin{bmatrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \\ \end{bmatrix} \quad H_3=\begin{bmatrix} 1 & -2 & 1 \\ -2 & 4 & -2 \\ 1& -2 & 1 \\ \end{bmatrix} \quad H_4=\begin{bmatrix} 0 & -1 & 0 \\ -1 & 5 & -1 \\ 0& -1 & 0 \\ \end{bmatrix} H2=⎣⎡−1−1−1−18−1−1−1−1⎦⎤H3=⎣⎡1−21−24−21−21⎦⎤H4=⎣⎡0−10−15−10−10⎦⎤
Laplacian锐化边缘提取
经过Laplacian锐化后,我们来分析几种变形算子的边缘提取效果: H1,H2的效果基本相同,H3的效果最不好,H4最接近原图。
Wallis算法
考虑到人的视觉特性中包含一个对数环节,因此在锐化时,加入对数处理的方法来改进。
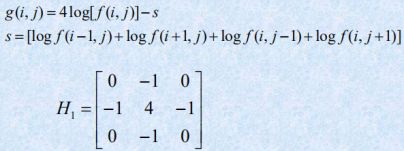
在前面的算法公式中注意以下几点:
1)为了防止对0取对数,计算时实际上是用 l o g ( f ( i , j ) + 1 ) log(f(i,j)+1) log(f(i,j)+1);
2)因为对数值很小 l o g ( 256 ) = 5.45 log(256)=5.45 log(256)=5.45,所以计算时用 46 ∗ l o g ( f ( i , j ) + 1 ) 46*log(f(i,j)+1) 46∗log(f(i,j)+1)。 (46=255/log(256))
算法特点:
Wallis算法考虑了人眼视觉特性,因此,与Laplacian等其他算法相比,可以对暗区的细节进行比较好的锐化。
3)一阶与二阶微分的边缘提取效果比较
以Sobel及Laplacian算法为例:
- Sobel算子获得的边界是比较粗略的边界,反映的边界信息较少,但是所反映的边界比较清晰。
- Laplacian算子获得的边界是比较细致的边界。反映的边界信息包括了许多的细节信息,但是所反映的边界不是太清晰。
bingo~ ✨ 如果我们不再把永恒看作时间上的无穷无尽,而是看作一个超越时间的状态,那么,永恒的生命属于那些活在当下的人。