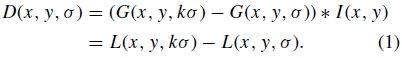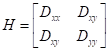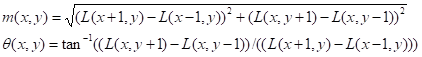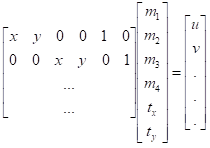此部分是计算机视觉部分,主要侧重在底层特征提取,视频分析,跟踪,目标检测和识别方面等方面。对于自己不太熟悉的领域比如摄像机标定和立体视觉,仅仅列出上google上引用次数比较多的文献。有一些刚刚出版的文章,个人非常喜欢,也列出来了。
33. SIFT
关于SIFT,实在不需要介绍太多,一万多次的引用已经说明问题了。SURF和PCA-SIFT也是属于这个系列。后面列出了几篇跟SIFT有关的问题。
[1999 ICCV] Object recognition from local scale-invariant features
[2000 IJCV] Evaluation of Interest Point Detectors
[2006 CVIU] Speeded-Up Robust Features (SURF)
[2004 CVPR] PCA-SIFT A More Distinctive Representation for Local Image Descriptors
[2004 IJCV] Distinctive Image Features from Scale-Invariant Keypoints
[2010 IJCV] Improving Bag-of-Features for Large Scale Image Search
[2011 PAMI] SIFTflow Dense Correspondence across Scenes and its Applications
翻译
基于尺度空间的不变关键点的不同图像特征——http://tongtianta.site/paper/56811
作者:DAVID G. LOWE
于2004年授权国际计算机视觉杂志出版。
摘要 -本文旨在阐述一种方法,这种方法可以通过提取不同的不变特征来可靠地匹配不同物体或景象的图像。这些特征对于图像尺度变化和旋转来说是不变的,而且在通过在3D空间大范围的投射、扭曲变化,加噪处理,光照改变,进行的匹配仍表现出健壮性。就算只取其中一个特征也很可能从数幅图像的众多不同特征中找到其正确匹配,由此可见,这些特征具有很强的区分性。本文也阐释了一种利用这些特征点进行物体识别的方法。它是通过对已知物体大量特征中的各个不同特征进行匹配来达成识别的,它利用快速就近运算法则和霍夫变换来辨别单一物体特征群,并最终用最小二乘法来确定一致性参数。这种方法可以很好地识别出混杂和拥塞中的目标,并完成及时处理。
1 介绍
图像匹配是计算机视觉领域中很多问题的基础,包括物体或景象识别,多重图像的3D结构复原,立体空间的一致性查找,还有运动跟踪。本文描述的图像特征,拥有很多适特性,它们可以用于匹配同一物体或景象的图像。这些特性在图像缩放和旋转情况下拥有不变性,在光照变化和3D的拍摄角度变化下拥有部分不变性。它们在时域和频域都拥有良好的适用性,可以有效排除混杂、拥塞、噪声带来的干扰。大量的特征可以利用一些高效的算法从一些典型图像中提取。补充一点,这些特征是具有高度区分性的,就算只取其中一个特征也很可能从数幅图像的众多不同特征中找到其正确匹配,这就为物体或景象的识别创造了条件。
最开始先进行一次初始检测,然后只对通过检测的局部进行更精细的检测,这样就可以最大程度地减小运算的花费。下面是生成这些图像特征的主要步骤:
1.尺度空间极值检测:算法的第一步是检测所有的尺度和整幅的图像。通过高斯函数变换来提取出潜在的具有尺度、方向不变性的兴趣点。
2.关键点定位:在每个候选的位置上,通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度。
3.方向的确定:基于图像局部的梯度方向,分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换,从而提供对于这些变换的不变性。
4.关键点描述:在每个关键点周围的邻域内,在选定的尺度上测量图像局部的梯度。这些梯度被变换成一种描述,这种描述允许比较大的局部形状的变形和光照变化。
这种方法被命名为Scale Invariant Feature Transform (SIFT),它将图像数据变换成一系列对于尺度具有不变性的特征。
这种配准方法的一个很重要的地方就是它在整幅图像的各个尺度和方位产生了大量的特征。一个典型的500×500像素的图像将会给出上至大约2000个稳定的特征(尽管这个数字取同时决于图像内容和变量参数选择)。所以对于图像识别,特征点选取得是否合适就尤为重要,为了更加可靠,就要求,要对一个微小物体辨认,至少要有3个特征被正确地匹配。
对于图像配准和鉴别,首先从一组图像中提取SIFT特征并以此作为基准。然后把新的图像的每个特征点分别与前面基准图像中所提取的特征点进行比较,比较其特征向量的欧氏距离,从而找到候选匹配特征。本文将讨论面对大量数据,如何利用快速就近运算法则高效地进行这种配准。
关键点描述符是具有很强的区分性的,它很有可能仅仅通过单一一个特征就从巨量特征中找到其正确的匹配。然而,在对于两幅不同图的配准,背景中许多特征是没有其正确匹配的,这就必将产生很多错误的匹配混杂于正确匹配中。而我们可以通过鉴别关键点参数,找出那些形状,位置,尺度,方向与新图一致的,把它们提取出来,这些就是正确的匹配了。好几个特征都是偶然的错误匹配的概率是远低于单一一个特征偶然错误匹配的概率的。所以这些完全匹配的匹配簇可以通过执行一个高效的哈希表的整体霍夫变换来迅速确定。
每一个的3个或者更多的与实物或其形态一致的特征组成的特征簇将进行下一步更深层次的精细配准。首先,对大致的形态仿射使用最小二乘估计。任何其他的与该形态一致的图像特征将被鉴别,轮廓线被丢弃。最后,进行更精细的算法,计算特定特征的配准概率,给出确切的可能的错误匹配的匹配度和数量。那些通过所有这些检测的匹配将被认为具有较高的可信度。
2 相关研究
通过用一组兴趣点来进行图像匹配的发展可以追溯到Moravec 1981年用一个边沿探测器在立体匹配方面的研究。这个Moravec 探测器后来被Harris 和Stephens后来在1988年进行了发展,使得它在图像微小变化和区别不大情况下的配准更加有效。1992年,Harris 还展示了它在运动复原中,高效动态捕捉和3D重建方面的价值,从此,Harris 探测器被广泛应用于许多其他的图像配准方面的工作。尽管这些对特征进行探测的探测器被叫做边沿探测器,但它们并不只是寻找图像中的边沿部分,而是探测在各个方向和已定尺度上的所有的拥有较大梯度的部分。
刚开始的应用主要是应用于立体合的短程移动捕捉,但是随后该研究扩展到了更复杂的领域。1995年Zhang et al. 证明了即使在更大的图像变化下,也可以通过利用关联窗口选择待配准图中相似部分来对Harris边沿进行匹配。通过求解一个描述两幅刚性变换景象的几何约束的基础矩阵,移除掉与大多数匹配不相一致的错误匹配后,那些离群值就被去除了。其实,在Zhang et al.发表这个证明的同时,1995年Torr也发表了类似的关于大范围波动的运动图像配准的研究学说,在他的学说里,图像中刚性物体的运动被用来建立几何约束以促使去除掉离群值。
其实在这方面研究上真正取得突破性进展的是1997年Schmid和 Mohr 所做的工作,他们展示了基于局部不变特征的匹配是可以通过将一个特征点与整幅图像进行比较而拓展到所有的图像识别领域的。他们也引用了Harris边沿来寻找关键点,但与开一个关联窗口进行匹配所不同的是,他们运用了局部图像的圆周不变描述符。更深一步,他们论证了复杂的特征匹配是可以通过鉴别匹配特征不变簇来实现混杂、拥塞图像的一般性匹配的。
因为Harris边沿探测器对图像尺度的变化是非常敏感的,所以它是不能用来做不同大小图像的匹配的。本文作者Lowe在1999年的所做的早期工作就是使局部特征点在空间尺度变化下的也具有不变性。这些研究开发了一个新的局部描述符,它就可以提供更多的鲜明特征而却对参照图像类似3D视角的变化并不敏感。本论文对此进行了更加深入的探索和分析,也展示了许多在稳定性和特征不变性方面的改进。
先前出现了大量的关于论证尺度变化稳定性的研究。最初是1984年Crowley 和Parker所做的研究,他们陈述了在尺度空间中峰值的标识,然后把它们关联到一个树状结构中去。这个树状结构可以随后用来在任意尺度变化下的图像间做匹配。近期更多的Shokoufandeh,Marsic 和 Dickinson1999所做的基于图标来进行匹配的研究则是提供了更好的利用小波参数的特征描述符。而Lindeberg1993、1994年更加深入地对寻找恰当的、一致的尺度空间进行特征探测问题进行了探索。他把此问题描述为尺度选择,下面我们将要用到他的相关结论。
近期出现了大量的关于拓展局部特征对于全仿射变换不变性的研究 (Baumberg,2000;Tuytelaars 和 Van Gool,2000;Mikolajczyk 和 Schmid,2002;Schaffalitzky 和 Zisserman,2002;Brown和 Lowe,2002)。这是考虑到在3D正投影的变化下平滑表面特征不变性的匹配,在大多数情况下是对一个局部仿射标架下的图像进行重复采样。然而,这些研究中没有一个是具有完善的仿射不变性的,他们由于难以承受扫描整个仿射空间的花费,刚开始就只能用一种不具有仿射不变性的方式选择初始的特征尺度和坐标位置。另外,仿射结构比具有尺度不变性的特征对噪声要更加敏感,所以实际上仿射特征的可再现性比尺度不变特征的要小,除非仿射失真有超过平面的40度的倾斜(Mikolajczyk,2002)。广义仿射不变性可能对于许多应用领域并非十分重要,比如为了捕捉3D物体的非平面变化和拥塞影响,某些实验角度最好是每旋转30度一个(意味着辨识能力在最接近的实验角度的15度内)。
本文所讲述的方法虽然也并没有完全的仿射不变性,但它已有突破,关联特征点在局部描述符微小变换下相应的会有重大变化。这种方法不仅使得描述符在各种程度的仿射失真下更可靠地匹配,而且使得特征在空间3D视角的变化下的拥有更强的健壮性。除此之外,还有更加有效的特征抽取、更多特征的提取能力等优点不尽详述。另一方面,在大的视角变化下的二维平面匹配的仿射不变性对我们来说是一个很宝贵的资源,参照它来对空间3D视角下不变性进行更深入的研究以提高效率和稳定性不失为一种好的思路。
许多其他的已被用于图像识别的特征类型也可以添加到本文所论述的特征向量中用以在不同环境下进行更完善的匹配。一种特征是利用了图像中的轮廓或边缘,以使其不至于被背景中贴近物体边界的凌乱东西所干扰混淆。Matas等人在2002年证实了它们的最高稳定性的极值区域可以很可靠地提供大量的匹配特征。 Mikolajczyk等人在2003年进一步开发出一种新的描述符,它利用了局部边界而忽略了不相关的临近边界,使其具有了即使在窄小区域的边界上叠加有背景中的杂乱物体也能稳定地发现有用特征的能力。Nelson 和Selinger 在1998年利用基于图像轮廓归类的局部特征得到了的良好结果。类似地,Pope和Lowe在2000年利用了基于图像轮廓按等级分类的特征,这对缺乏详尽细节的物体尤其有效。
在关于视觉识别的研究历史上,所做的工作都是关于各种各样的可以被用来寻找特征的图像工具。Carneiro和Jepson在2002年描述了基于相位的局部特征来表示相位,而不是局部空间频率的级别,而这有可能提供更好的光照不变性。Schiele和Crowley在2000年提出了表示图像区域内检测分布的多维直方图的使用。这种类型的特征可能对于辨认复杂多变纹路物体尤其有效。Basri和Jacobs在1997年已经证明了提取局部区域边界对于视觉识别的价值。所纳入的其他有用属性还包括颜色,运动,图形背景辨别,区域的形状描述,以及立体纵深表示。局部特征的方法可以很容易吸收新的特征类型,因为额外的功能在它们提供了正确的匹配时,非常有助于提高健壮性,而没有提供这种正确匹配时除计算成本以外也不会有什么其他负作用。因此,未来的系统很可能会结合许多的特征类型。
3 尺度空间极值检测
正如简介里所介绍的,我们将会用高效的小波滤波法检测关键点来寻求将来会被进一步详细检测的候选域。关键点检测的第一步是寻求可以被用来在同样物体的不同取景角度下重复标识的空间和尺度。探测对图像尺度变换具有不变性的区域可以通过在所有可能尺度寻找稳定特征点来实现,运用一个被称作尺度空间(Witkin,1983)的连续尺度函数。
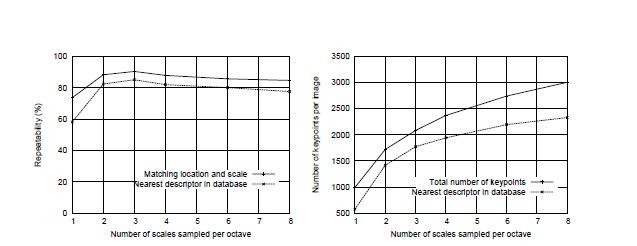
Koenderink(1984)和Lindeberg(1994)证明在一系列合理假定下唯一可能的尺度空间核是高斯卷积核。因此,图像的尺度空间(图像的尺度空间表达指的就是图像在所有尺度下的描述。)被定义成一个函数,L(x; y; σ),它是由一个变化尺度的高斯函数G(x; y; σ)与输入的图像I(x, y)卷积生成的:
L(x; y; σ) = G(x; y; σ) * I(x; y),
这里*代表卷积操作,其中
为了高效地探测到尺度空间中稳定的关键点区域,我们提出了(Lowe, 1999) 利用尺度空间极值通过高斯函数的差分与图像D(x; y; σ)做卷积,即由两个临近的不同不变常数因子k确定的尺度相减求得:
关于为何要选这个函数有多方面的原因。首先,它是一个计算效率极高的函数,例如对于平滑图像,L,需要在每一次尺度空间特征描述时被计算,而D在计算时仅仅是图像的简单相减。
图1:对于尺度空间的每一层,原始图像都被高斯算子重复卷积来计算出如图左所示的尺度空间图像。临近的高斯图像被相减得出高斯图像的差分图像,如图右边所示。在每一层图像被计算得出后,高斯图像则被2倍降采样,而后步骤类似。
需要补充说明的是,高斯差分函数是归一化的高斯拉普拉斯函数的近似,![]() ,是Lindeberg (1994)研究得出的。Lindeberg验证了因子为
,是Lindeberg (1994)研究得出的。Lindeberg验证了因子为![]() 的拉普拉斯算子的归一化要求完全的尺度不变性。在更详细的实验比较中, Mikolajczyk (2002)发现通过
的拉普拉斯算子的归一化要求完全的尺度不变性。在更详细的实验比较中, Mikolajczyk (2002)发现通过![]() 的最大最小值,相比于很多其它的这类函数,可以得到最稳定的图像特征,比如梯度、Hessian, 以及Harris边沿函数等。
的最大最小值,相比于很多其它的这类函数,可以得到最稳定的图像特征,比如梯度、Hessian, 以及Harris边沿函数等。
D 和 ![]() 的关系可以从热传导等式推知(参数用σ代替通常所用的t=
的关系可以从热传导等式推知(参数用σ代替通常所用的t=![]() ):
):
从这里我们能够看到![]() 可以通过无限差分计算逼近
可以通过无限差分计算逼近![]() ,即利用相邻尺度 kσ 和 σ的差分:
,即利用相邻尺度 kσ 和 σ的差分:
因此,
![]() 。
。
这体现了当高斯差分函数的尺度因一个常量变化而不同时,它本身已经满足了尺度不变性的拉普拉斯算子的![]() 尺度的归一化的要求。等式中的因子(k-1)是一个在所有尺度都不变的常量,因此不影响极值点的位置。近似误差也会随着k接近于1而趋于0,但是在实践中我们发现这种近似即使在尺度的很大变化下对极值点的探测和分布的稳定性仍然基本没有影响,例如取
尺度的归一化的要求。等式中的因子(k-1)是一个在所有尺度都不变的常量,因此不影响极值点的位置。近似误差也会随着k接近于1而趋于0,但是在实践中我们发现这种近似即使在尺度的很大变化下对极值点的探测和分布的稳定性仍然基本没有影响,例如取![]() 。
。
图2高斯差分尺度空间极值点
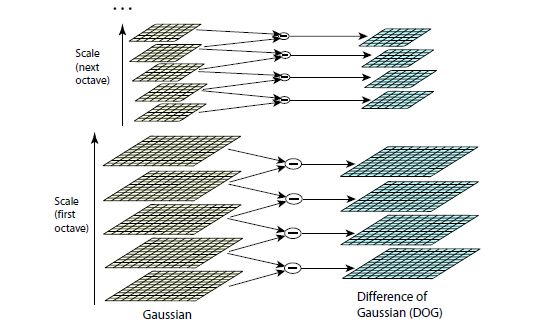
图2:高斯差分图像的最大最小值的检测是通过比较该像素点(如图中X)与其当前和临近尺度周围33范围内26个点(用圆圈表示)比较所得。
图1展示了一个计算D(x; y; σ)的高效方法。初始图像递增地卷积于高斯算子得出在尺度空间由k所分离出的图像,如图左列所示。我们选择把每一层尺度空间(例如将σ翻倍)分成整数阶,s,因此![]() 。我们必须为每一层计算s+3幅图像,这样最终的极值检测就能覆盖到整层图像了。相邻图像尺度相减来得到高斯差分图像,如图右列所示。第一层图像计算完成后,接着对第一层图像中的2倍尺度图像(相当于该层第一幅图像的2倍尺度)以每一行列的2倍像素距离进行降采样。关于σ采样的精度与先前初始层相比是没有区别的,然而计算量却大大减少了。
。我们必须为每一层计算s+3幅图像,这样最终的极值检测就能覆盖到整层图像了。相邻图像尺度相减来得到高斯差分图像,如图右列所示。第一层图像计算完成后,接着对第一层图像中的2倍尺度图像(相当于该层第一幅图像的2倍尺度)以每一行列的2倍像素距离进行降采样。关于σ采样的精度与先前初始层相比是没有区别的,然而计算量却大大减少了。
3.1 局部极值检测
为了检测出D(x; y; σ)的最大最小值,每一个采样点都要分别与其当前层周围8个相邻点,前一尺度、后一尺度的各自的9个点作比较(见图2)。只有与周围相比最大或最小的点才能被选作候选点。由于绝大多数采样点将被开始的几次检测淘汰,所以此次检测的计算量会非常小。
一个值得注意的地方是,采样的频率对于图像和尺度区域的极值检测要确实可靠。然而,我们证明得知是不存在这样的能检测出所有极值的最小采样间距的,尽管这些极值可以被无限逼近。我们可以设想一个画着一个白圈的黑板,它将会有唯一的一个尺度空间极大值对于的高斯差分函数圆心区域匹配于这个圆的大小和位置。而对于一个狭窄的椭圆,则将会有两个极大值分布在椭圆的两端。因为极大值的分布是一个关于图像的连续函数,所以对于某些中间拉长的椭圆,最大值就会由一个逐渐转换为两个。转换中最大值点则将各自逼近。
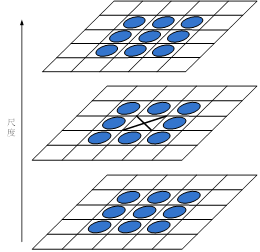
图3:第一张图的上面一条线显示了在同一位置和尺度随着每层采样数量的变化,重复检测的关键点的百分比随之的变化走向。下面一条线显示了其描述符正确匹配于基准库的关键点的百分比。第二幅图像展示了在典型图像中所检测到的关键点的总数量对于尺度采样数量的函数。
因此,我们必须解决精度换效率的问题。事实上,作为可见预期,再加上我们的实验证实,极值的逼近对于图像的小扰动干扰是相当不稳定的。我们可以通过试验一系列采样频率,利用实验数据确定最佳选择,在仿真匹配模拟中找到最可靠的试验结果。
3.2 尺度的采样频率
实验测定的最稳定极值采样频率如图3、图4所示。这些数字(还有本文中很多其他的模拟)的得出都基于一个真实的匹配任务,该任务围绕着一个集合了32幅从不同范围,包括外景,人脸,航拍照片,工业图像等真实图像的图像集进行(发现图像类型对结果几乎没有任何影响)。每个图像,都进行了一系列变换,包括旋转,缩放,仿射拉伸,改变亮度对比度,以及添加图像噪声。因为变化是合成的,所以就可以的准确地预测出原始图像中每个特征应该出现在转化后的图像的位置,使得测量每个特征点的正确再现性和定位精度成为可能。
图3显示了这些模拟结果,这些结果都曾用来检测每层尺度数目变化的影响,这里图像函数的采样先于极值检测。在这种情况下,每幅图像都是在任意角度、原始图像的0.2到0.9倍之间任意缩放比例中随机抽样的。降采样图像中的关键点是可以匹配到原始图像中去的,所以所有关键点的尺度都将能够出现在匹配图像中。此外,增加了1%的图像噪声,这意味着每个像素添加一个取自均匀分布[-0.01,0.01]中的随机数,而从其中像素值的范围是[0,1](相当于提供略少于6bit的图像像素精度)。
图4:图中的最上面一条线表示了在转换图像中可以被重复检测的关键点的百分比,作为每层图像的第一幅图像的前一图象平滑性的函数。下面一条线表示了相对于基准库正确匹配的描述符的百分比。
图3中的第一幅图的上面一条线表示了在转换图像中匹配的区域和尺度的被检测的关键点的百分比。对于本文所有的例子,我们定义匹配尺度为正确尺度的![]() 倍范围内,定义匹配位置为在σ像素范围内,这里σ是关键点尺度(定义方程式(1)高斯差分函数的最小高斯核的标准差)。图中的下面一条线展示了第六章中所讲的利用临近匹配法所求得的正确匹配于基准库40000个关键点的关键点数量(这表示了一旦关键点被可重复性定位,它就很有可能会被以后的识别和匹配所用到)。所有的这些都证明了,当每层图像取3个尺度时,就可以获得最高的可重复性,这也是通用于全文的所有实验的尺度采样数。
倍范围内,定义匹配位置为在σ像素范围内,这里σ是关键点尺度(定义方程式(1)高斯差分函数的最小高斯核的标准差)。图中的下面一条线展示了第六章中所讲的利用临近匹配法所求得的正确匹配于基准库40000个关键点的关键点数量(这表示了一旦关键点被可重复性定位,它就很有可能会被以后的识别和匹配所用到)。所有的这些都证明了,当每层图像取3个尺度时,就可以获得最高的可重复性,这也是通用于全文的所有实验的尺度采样数。
这可能看起来不可思议,可重复性不随着尺度采样数目的增加而继续提高。原因就是它导致了更多的局部极值点被探测,但是这些极值点在总体上会趋于不稳定,因此在转换图像中就更不容易被检测。这点在图3中表现了出来,它展示了在每幅图象中被检测和正确匹配的关键点的平均数目。
关键点的数目随着尺度采样的数目增加而增加,总的正确匹配的数目也随之增加。由于物体的识别成功与否一般情况下都更多的取决于正确配准的关键点的数目,而不是正确匹配所占的比例,所以对于很多应用,用更多数量的尺度采样将会达到更好效果。然而,运算的花费也会随着这个数目的增加而增加,所以对于本文提到的各个实验,我们选择了每一层3次的尺度采样数。
总之,这些实验展示了尺度空间高斯差分函数会产生大量的极值点,而检测所有的这些点必将开销巨大。所幸的是,我们即使只是对尺度进行粗采样也能探测到最稳定和最有用的关键点子集。
3.3 空间区域的采样频率
正如我们所确定尺度空间每层的采样频率一样,我们必须确定关于平滑性尺度的图像区域的采样频率。我们已知极值可以被无限逼近,所以同样的,我们还需要做一个采样频率和检出率之间的权衡。图4展示了一个实验结论,初始平滑性值,σ,是适用于建造尺度空间前每层图像中的每阶图像的。需要再次强调的是,上面一条线表示了关键点检测的可重复性,结果证明,这种可重复性会跟着σ持续增长。然而,就效率而言,用一个较大的σ会产生很大开销,所以我们选择使用σ=1.6,它能提供接近于最优的采样率。这个值应用于本文全文,也被作为图3的结论。
当然,如果我们在极值检测前对图像进行预平滑化,我们将很可能会错过最高的空间频率。因此,为了更好的利用输入图像,该图可以被拓展产生比原始图像本应产生的更多的采样点。我们在建造金字塔第一级之前利用线性插值方法2倍化输入图像。类似的,利用对原始图像补偿像素点的方法也同样行之有效,图像的倍化将会使匹配效果更好。我们假设原始图像的模糊度至少为σ=0.5(为了不出现明显的混淆现象的最小值),因此,由于倍化的图像中其新产生的像素间隔,σ=1.0。这意味着在尺度空间第一层建造之前,需要添加一些平滑性。图像倍化基本上是以因子4的程度增加了稳定关键点的数目,但是在进行更大扩展时却没有发现其有更显著的改善。
4关键点的精确定位
一旦一个关键候选点通过与邻近像素点比较而被选出,第二步就是进行所在区域、尺度、主曲率的邻近数据的精确配准。这些信息将使拥有较低对比度(因此对噪声是非常敏感的)或者集中分布在边沿附近的点被淘汰。
这种方法初步的实施(Lowe,1999)只是对于分布在中央采样点位置和尺度的关键点。然而,最近,Brown已改进了这种方法(Brown和Lowe,2002)使它可以适应于对局部采样点的3D二次函数,从而确定内插值最大分布,他的实验结论展示了这将会给匹配和稳定性带来实质性进展。他的研究利用了尺度空间函数的Taylor展开(展开到二次), D(x; y; σ),变换使得起始点在采样点上:
这里D及其派生函数在采样点被计算,![]() 是这一点的余项。极值的分布,
是这一点的余项。极值的分布,![]() ,被这个x的函数的派生函数,设x为0而得到,给出:
,被这个x的函数的派生函数,设x为0而得到,给出:
图5:此图显示了关键点的选择阶段。 (a)233x189像素的原始图像。(b)最初的由高斯差分函数的最大值和最小值确定的832个关键点的分布。关键点显示为向量,表示的尺度,方向和位置。(c)通过最低对比度阈值,剩余729个关键点。(d)再经过主曲率的阈值淘汰,最后剩下的536关键点。
正如布朗说提到的,Hessian和D的派生函数就是近似地在对相邻采样点差分。由此产生的3x3的线性系统可以以最低的成本解决问题。如果偏移![]() 在任何尺度上大于0.5,那么就意味着极值是临近于另外一个不同的采样点。在这种情况下,就改变采样点,来代替此点。最终偏移
在任何尺度上大于0.5,那么就意味着极值是临近于另外一个不同的采样点。在这种情况下,就改变采样点,来代替此点。最终偏移![]() 被添加到采样点的位置上,以得到极值点位置的内插值估计。
被添加到采样点的位置上,以得到极值点位置的内插值估计。
在极值点,函数值D(![]() )用于淘汰低对比度的不稳定极值。这可以通过将等式(3)替换为(2)而得到,如下
)用于淘汰低对比度的不稳定极值。这可以通过将等式(3)替换为(2)而得到,如下
对于本文中的实验,所有极值点的![]() 值小于0.03的都将被舍弃(前面,我们假设图像像素值取值范围为[0,1])。
值小于0.03的都将被舍弃(前面,我们假设图像像素值取值范围为[0,1])。
图5展示了在一幅自然图片上的关键点选择的效果。为了避免太多的凌乱干扰,我们用了一张233×189的低分辨率图像,关键点以向量形式给出,指示其位置,尺度以及每一个关键点的主方向(方向的确定将会在下面详细给出)。图5(a)展示了原始的图像以作为后面图像的对比参照。图5(b)展示了所有检测到的由高斯差分函数最大最小值所确定的832个关键点,而(c)展示了经过![]() 值小于0.03条件淘汰后的剩余的729个关键点。最后(d)部分的工作下面章节将会讲述。
值小于0.03条件淘汰后的剩余的729个关键点。最后(d)部分的工作下面章节将会讲述。
4.1消除边缘反应
为了稳定,单单只是淘汰掉低对比度的关键点是不够的。高斯差分函数会产生较强的边缘响应,即使边缘确定得很差,所以对于少数量的噪声也是不稳定的。在高斯差分函数的中有一个不好的峰值它在横跨边界时有一个重大的曲率变化,但在顺延边界方向的却只是一个小的曲率。主曲率可以在关键点的位置和尺度上通过一个2x2的海森矩阵计算得出,H:
派生函数的估计可以通过相邻采样点的求差得出。
H的特征值与D的主曲率是成比例的。借用Harris和Stephens(1988)所使用的方法,我们可以避免完全计算出其特征值,因为我们只关注他们的比率。设α是最大特征值,而β是最小特征值。然后,我们可以计算出特征值的总和算出H的迹,计算其行列式:
![]() ,
,
![]() 。
。
行列式在某些极少数情况下会出现负值,这时曲率会出现奇异的特点,所以该点将会因为不是一个极值点而被舍弃。设 r 是最大特征值与最小特征值之比,因此,ɑ = rβ。然后,
只取决于两个特征值的比率,而不是它们各自的值。当两个特征值相等时,上式取得最小值;随着r的增加,上式的值也增加。因此,要检查主曲率的比率是否在某一阈值 r 之下,仅需要检查
这是非常高效的计算,测试每一个关键点只要求进行少于20个的浮点计算。在本文的实验中,使用的r=10,从而消除了那些主曲率比值大于10的关键点。从图5(c)到(d)的过渡显示了此操作的效果。
5统计主方向
根据局部图像特性,利用统一标准给每个关键点分配一个与其相适应方向,这些关键点描述符可以与表示出与这个方向的联系,从而对于图像的旋转变化具有了不变性。这种方法与Schmid和Mohr(1997年)的方向不变性描述符形成强烈反差,在他们的方法中,每一个图像属性都是基于旋转不变量度而来的。他们这种方法的缺点是,它限制了可以使用的描述语,并且由于它没有要求所有的测量都满足旋转一致性,从而丢弃了一些图像信息。
通过用许多用各种方法标识局部方向的试验,找到下面这种方法能够给出最稳定的结果。关键点的尺度用于选择尺度最接近的高斯平滑的图像L,以便使所有的计算都在尺度不变的方式下进行。而对于每个图像样本L(x,y),在这个尺度上,梯度,m(x,y),和方向,θ(x,y),则是根据像素差异被预先计算的:
然后利用高斯空间中每个特征点一定邻域内采样点的梯度方向创建一个方向直方图。直方图以10度为一个单位将360度分成36个柱。根据每个采样点的梯度值以及一个 σ 等于其本身尺度1.5倍的高斯判定圆形窗将其归入适当的柱。
方向直方图中最大峰值作为特征点梯度的主方向。直方图中的最大峰值是要被检测的,然后直方图中量值达到主峰值80%以上的局部峰值方向也创建一个特征点。因此,对于拥有相似显著性的多峰值特征点就会有多个在同一位置统一尺度而方向却不同的特征点。虽然仅有15%的位置会产生这种情况,但这种多方向特征点的方法对匹配的稳定性贡献很大。最终,依据近似代表每个峰值的3个柱状图值拟合一条图线来修正峰值位置以达到更好的精确性。
图6显示了在不同数额的图像噪声下的位置,尺度,定向分配的实验稳定性。如同之前的图像以随机的数值进行旋转和尺度变换。顶曲线显示了关键点的位置和尺度分配的稳定性。第二曲线则显示了当要求方向分配在每15度算一分度时的配准稳定性。正如前两行之间的差距所展现的,即使在增加±10%像素噪声(相当于一个提供小于3位精度的摄像头),方向分配仍然保持着95%的准确性。测量的方向正确匹配的方差是2.5度左右,增加10%的噪音后上升到3.9度。图6中的最底下的图线显示了对于一个40000关键点库的关键点描述符正确匹配的最终精度(下面即将讨论)。由图可知,SIFT特征是可以忍受大量像素噪音的,而所出现的匹配错误则主要是由于初始位置和尺度的检测。
图6:图中的顶线显示了一个关于像素噪声的函数,它表示了可重复探测关键点的位置与尺度的百分比。次线显示了对方向一致性也有要求的可重复性。而底线则显示了对于大型库最终所能正确匹配的描述符的百分比。
6局部图像描述符
先前的操作为每个关键点指定了图像的位置、尺度和方向。这些参数利用一个可重复的局部二维坐标系统来描述局部图像区域,因此这些区域对这些参数具有不变性。下一步是计算得出局部图像区域的具有强区分性的描述符,使其尽可能地对于光照和3D视角的改变保持不变性。
一个显而易见的方法是在适当尺度的关键点周围对局部图像强度进行采样,利用一个相关性归一化方法去匹配它们。然而,简单的图像碎片的相关关系对于仿射或3D的视角变化或者非刚性变形是非常敏感的,这就导致了图像配准的失败。而一个更好的方法被Edelman、Intrator 和Poggio(1997)论证。他们提出图像是基于生物视觉模型的,特别是初级视觉皮层的复杂的神经元。这些复杂的神经元会对特定的方向和空间频率的梯度产生响应,但此梯度的位置在视网膜上是允许小范围波动的,而并非精确定位。Edelman等人推测,这些复杂的神经元的功能就是使3D物体在一系列的视角上都能被匹配和识别。他们已经利用各种物体和动物形状的3D计算机模型进行了详细的实验,证明了在允许位置的小范围波动情况下的梯度配准对3D变换会产生良好的辨认效果。例如,通过使用复杂的细胞模型,在以20度为旋转深度的三维物体的识别精度,其梯度相关性从35%增加至94%。我们下面所描述的实施方法就是受这种思想的启发,但允许使用不同的运算机制进行位置转变。
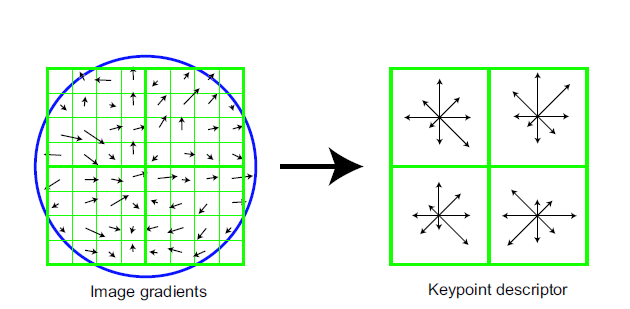
图7:创建一个关键点描述符,首先要对关键点周围的每一个采样点进行梯度幅值和方向的计算,如左图所示。它们通过高斯窗口进行加权,覆盖一个圆圈来表示。然后将这些采样点累加到方向直方图中来描述这个4×4区域的内容,如右图所示,每个箭头的长度与相应方向的附近区域内的梯度幅度的总和相一致。此图显示了从8×8的采样点组计算成2×2的描述符阵列,而在本文的实验中使用的是从一个16×16的采样点组阵列计算成4×4的描述符阵列。
6.1广义的代表性
图7说明了关键点描述符的计算过程。首先从关键点的位置周围对图像梯度的大小和方向进行采样,用关键点的尺度为图像选择高斯模糊水平。为了实现方向不变性,描述符的坐标和梯度的方向与关键点的方向是旋转相关的。为了提高效率,如第5章所述,金字塔各级的梯度将被预先计算。而后,如图7所示,在每个采样位置用小的箭头来代表它们。
高斯加权函数的参数σ等于描述符窗口宽度的一半,用于给每个采样点的幅度分配权重。这点用图7左边的圆形窗口中进行了说明,当然,权重是连续递减的。此高斯窗口的目的是为了避免在窗口区域小的变动会引起描述的突然变化,同时也使远离描述符中心的梯度能够不被过分强调,因为就是这些在很大程度上导致了匹配的错误。
图7右侧展示了关键点描述符。通过在一个4×4区域创建方向直方图,关键点描述符便能够容忍梯度位置上的显著变化。该图为每个直方图显示了8个方向,而直方图的显著程度用分别每个小箭头的长度表示。左侧的梯度采样可以用于4个样品位置,同时作用于如右图所示的4个柱状图,从而实现容忍更大局部位置变动的目标。
非常重要的一点是要避免所有边界描述符突然变动的影响,因为采样从一个柱状图到另一个柱状图,从一个方向到另一个方向的变化是连续的。因此,使用了三线性插值来把每个梯度采样值分配到各个相互临近的柱状图格子中。换句话说,每个格子中的项都乘了对应各自程度的1-d的权重,其中d是在每个柱状图格子单元中采样点到格子中心的距离。
该描述符是由一个向量形成的,该向量包含了所有的方位直方图项值,对应于图7右侧的箭头的长度。这个图像展示了一个2×2阵列的方位直方图,而下面的实验表明最好的结果,是在每个4×4的8方向直方图列阵上达到的。因此,本文中的实验采用了一个4×4×8=128维的特征向量来表示每个关键点。
最后,我们来改进特征向量以减少光照变化的影响。首先,向量被归一化。图像对比度中每个像素值都乘了一个常量,因此,图像对比度的变化也会给梯度乘上一个相同的常量,所以这种对比度的变化将会被向量的归一化所取消。如果一个图像的每个像素都添加了一个常量,那么它的亮度变化不会导致梯度值的变化,因为它们计算的是像素间的差异。因此,在光照仿射变化中的描述符是不变的。然而,非线性光照变化也会由于相机饱和度或者光照变化在不同方向不同程度对3D表面施以影响而引起。这些影响可能会导致某些梯度值的大的变化,但很少会影响梯度的方向。因此,我们可以设定一个阈值,让单位特征向量的幅度不大于0.2,然后再把它归一化,以此来降低对梯度值的大的影响,这意味着为大梯度值的匹配已不再是那么重要,转而去重视其方向的分布。0.2的值是我们通过利用同一物体不同光照强度的图像进行实验而确定的。
6.2描述测试
我们可以利用两个参数来表示这个描述符的各种复杂情况:直方图中的取向数量,r,n×n方向直方图中的宽度,n。描述矢量的最终大小是r×n×n。随着描述符复杂程度的增长,在大型的数据库中它们将会被更好地区分,但这也会导致其在形状扭曲和闭塞上更加敏感。
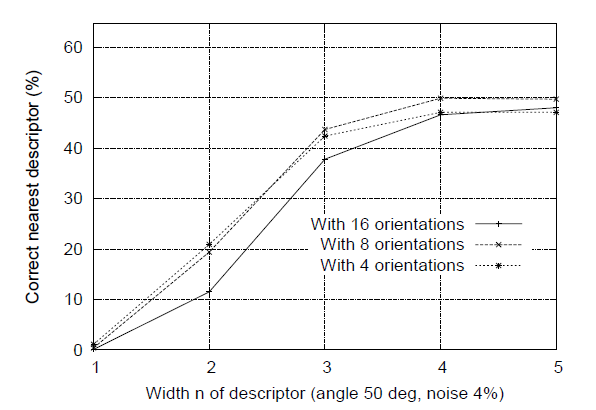
图8给出了方向数量和描述符大小变化下的实验结果。图像生成于视角的转换,平面相对于离观察者倾斜出50度角,并添加4%的图像噪声。这已接近了可靠匹配的极限,因为只有在这些更为困难的情况下,才更能显示出描述符是最重要的。结果显示了在40000关键点的库中,找到正确的匹配的单一最接近的关键点的百分比。图表显示一个单一方向的直方图(n= 1)在分辨力方面做的很差,但紧接着,我们又对8方向的4×4阵列直方图进行试验,结果改善了很多。此后,再加入更多的方向或更大的描述符则实际上会损害匹配,因为它会使得描述符更对失真更加敏感。对于其他的视角改变程度和噪声程度来说,结果是相似的,尽管在一些简单的情况下,如果我们用5×5阵列直方图和更高的描述符的大小,区分性会继续改善(已有很高的水平)。我们在本文通篇使用一个8方向4×4阵列直方图来描述符,生成128维的特征向量。虽然描述符的维数似乎看起来很高,但我们发现在一系列的匹配任务上,它总是能够比低维的描述符表现得更好,并且当我们利用了下文将要讲的大致最近匹配方法后,计算量仍能维持在较低的水平。
图8:该图表示的函数是以n×n描述符的阵列宽度和以每个柱状图的方向数作为自变量的能够在具有40000关键点库的图像中正确匹配的关键点百分比的函数。该图所计算的图像是具有50度仿射视角变化和添加4%噪音后的图像。
6.3仿射变化的敏感性
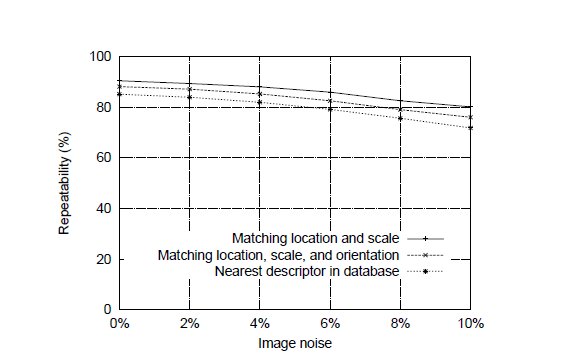
图9测试了描述符对仿射变化的敏感性。图表显示了随着观察者观察角度的变化,关键点位置和尺度选择,以及方向分配,还有最接近描述符与图像的配准可靠性的变化。
可以看出,每次计算的所得的可重复性随着仿射失真的增加而降低,但在变化角度超过五十50度时,最终匹配精度仍保持在50%以上。
为了在更高程度的角度变化下实现可靠的匹配, 一种仿射不变的探测器应该可用于在图像区域进行选择和重复取样,正如在第2章讨论的那样。如前所述,这些方法都不是真正的仿射不变,因为它们一开始都是通过非仿射不变的方式确定的初始特征的位置。最接近于仿射不变的方法,是Mikolajczyk(2002年)提出和详细实验的Harris仿射探测器。他发现,在超出大约50度的角度变化下该探测器的关键点可重复性是低于这里所给的方法的,但是在超出70度角时,它仍保留了接近40%的可重复性,即在极端的仿射变化下会有更好的表现。而其缺点是计算成本更高、关键点数量的很少,由于噪声干扰下不变仿射标架的错误分配,在小的仿射变化下的稳定性较差。在实践中,三维物体的旋转允许的范围是绝不只是平面的,所以仿射不变性通常不是视角变化下配准的限制因素。如果需要广泛的仿射不变性,如已知一个表面是平面的,那么一个简单的解决办法就是采用Pritchard 和 Heidrich (2003年)的方法,额外的SIFT特征从配准图像的4次仿射转换描述中产生,相当于60度的视角变化。这使得图像识别能够运用标准的SIFT特征而不需要额外开销,但结果是特征库的大小将会增加3倍。
图9:该图表示仿射变化下,检测关键点位置方向并最终匹配数据库的稳定性的变化关系。仿射失真度是用平面的角度旋转来实现的。
6.4匹配大型库
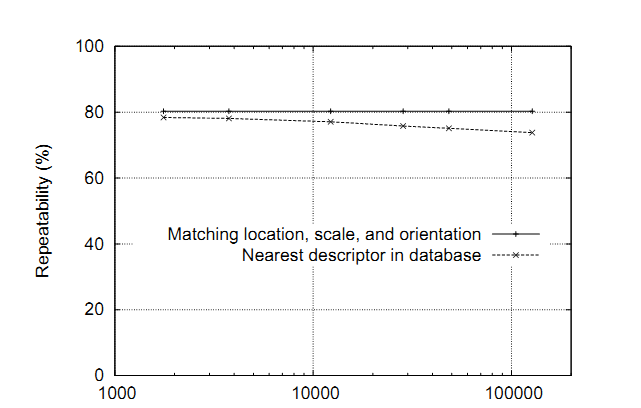
剩下的一个探测显著特征的重要问题就是匹配质量的可靠性作为库中已匹配特征数量的函数是如何变化的。本文中的例子大部分都是使用大约40,000个关键点的32幅的图像库生成的。图10展示的就是匹配的可靠性是如何因特征库的大小而变化的。而此图是使用的是更大的112幅的图像库生成的,除了一般的随机图像旋转和尺寸变化外还添加了30度的视角旋转和2%的图像噪声。
虚线表示在数据库中达到正确匹配的部分图像特征,作为数据库大小的函数用对数刻度表示。最左边的点匹配的只是单一图像中的特征,而最右边的点是从112幅图所有特征的库中选择合适的匹配。它可以看出,匹配的可靠性会随着错误匹配数量的增加而降低,但所有迹象都表明,巨大的库下将会继续发现更多正确的匹配。
实线是在转换图像中位置和方向上都正确配准的被识别的关键点的百分比,所以只有这些点才可能在库中有其匹配的描述符。这条线之所以是平的原因是这项测试覆盖了整个数据库的每一个值,而仅有的不同的部分是错误的匹配。有趣的是两条线之间的差距很小,表明匹配失败是更多的由于初始特征位置和方向分配的问题而不是特征的独特性,甚至对于大容量库也是这样。
数据库中的一些关键点点(对数标度)
图10:虚线表示的是正确匹配于库的关键点的百分比的关于库容量的函数(使用一个对数标度)。实线表示的是被分配到正确的位置、尺度、和方向的关键点的百分比。该图像拥有随机尺度和角度的变化,一个30度的仿射变化,还有匹配前予其添加的2%的图像噪声。
7目标识别的应用
本论文的主要目的是具有独特性的不变关键点,如上文所描述的。要阐述其应用价值,我们现在将会做一个简短的描述,描述其用于混杂和拥塞环境中的图像识别。更多关于应用这些特征进行识别的详细描述可在其他文件中找到(Lowe,1999;Lowe,2001;Se,Lowe and Little,2002)。
执行目标识别,第一步要把各关键点独立地与配准图像所提取的关键点的库进行匹配。最初这些匹配,可能因模棱两可的特征或背景杂波产生的特征,而使得其中许多匹配是不正确的。因此,至少3个特点的特征簇能够一致地匹配于一个物体或形态则是第一个需要被鉴定的,因为这样的集群的正确匹配概率比单个的高得多。然后,每个群集通过一个具体的几何变化模型进行检测,决定是接受还是拒绝这个匹配。
7.1 关键点匹配
为了给每个关键点寻找其最好的候选点,我们需要在配准图像关键点库中鉴别出它的最接近项。关于最接近项我们可以这样来解释,即对于第6章讲到的不变描述符向量,欧氏距离最小的关键点。
距离的比率(最近/次最近)
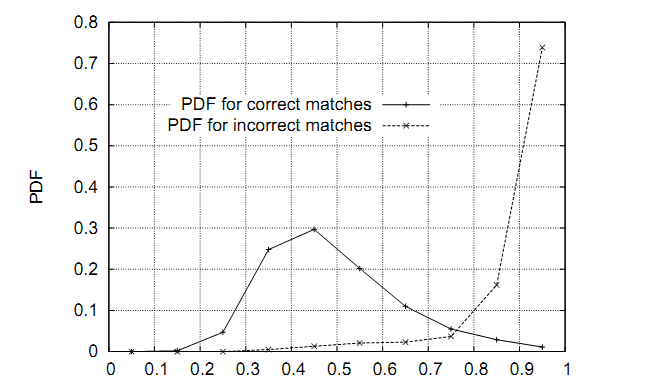
图11:一个点的匹配是正确的可能性可以通过计算其与最近项距离和与次近项距离的比值来确定。对于一个40000关键点的库,实现表示的是正确匹配比率的概率分布函数,而虚线表示的是错误匹配比率的概率分布函数。
然而,图像中的许多特征在配准库中是没有任何的正确的匹配,因为它们或来自背景杂波或在配准图像中未被检测到。因此,找一种方法来丢弃掉在库中没有的任何好的匹配的特征是有用的。在与最接近的特征的欧氏距离上整体设置阈值并不十分有效,因为一些描述符的区分性比其他的要高得多。一个更有效的措施是比较最近项的距离与第二近项的距离。如果同一个的对象有多幅配准图像,已知最接近项是来自不同的对象,那么我们定义第二接近项作为最接近项,例如只使用已知的图像来抑制不同的对象。这个措施很有效,因为正确的匹配需要的最接近项要比错误匹配的最接近项更加接近以实现可靠的匹配。对于错误的匹配,由于特征维数较高,很有可能还能找到一些其他有类似的欧氏距离的错误匹配。我们可以认为第二接近的匹配提供了一个在此特征空间区域错误匹配密度的估计,同时也证实了特征模糊性的具体实例。
图11展示了把真实图像数据代入此法的所得值。正确或者不正确匹配的可能性密度函数通过每一个关键点最近与次接近比值的形式表现出来。最接近项匹配正确的匹配比上错误匹配,概率分布函数中间的比率更低。在我们的目标识别中,我们拒绝了所有大于0.8的距离比率,这样最终丢弃了大约90%的错误匹配和少于5%的正确匹配。这一图表是通过匹配拥有随机尺度方向变化,30度深度旋转,再加2%的画面噪音,拥有40000个关键点的图像生成的。
7.2 高效的临近点标定
现在已知的没有哪个算法能比穷举搜索更有效地在大尺寸的空间中精确探测到最接近特征点。我们关键点描述符有一个128特征向量,最好的算法,例如k-d树(Friedman 等,1977年)对于超过10维空间的穷举搜索也不能提供加速。因此,我们采取了一个近似算法,叫做Best-Bin-First(BBF)算法(Beis和Lowe,1997年)。这是一种近似,意味着他返还的最接近项是具有很高可能性的。
BBF算法用了一个改良k-d树排序方式的搜索算法以使得在特征空间内的块是以与目标位置距离最近的顺序而被搜索。这个优先寻找排序是Arya和Mount1993年首次试验的,并且他们对它的计算方法进行了进一步的研究(Arya 等,1998)。为了快速决定搜索顺序,这种排序方法用了一个堆的优先排队法。当搜索到的最接近块达到一定数量后,我们就放弃更进一步的搜索,这样,我们就可以以低成本寻找到近似的答案。我们在实际计算时,在找到200个最近项后就停止搜索了。在一个100000关键点的库中,这样的方法在最近项的搜索中提供了两个数量级的加速,而同时丢失了少于5%的正确匹配。BBF算法的有效性原因之一是我们只考虑最接近点与第二接近点距离比率小于0.8匹配(如前一章所讲的那样),而且因此没有必要精确处理那些相邻点距离十分接近的最困难情况。
7.3 霍夫变换集簇
为了最大限度地对小的和高阻塞的对象进行识别,我们希望能通过尽可能少的特征匹配来辨别目标。我们发现最少可以通过3个特征就可能进行可靠地识别。一个典型的图像会包括2000或者更多的特征,这些特征可能来自于许多不同的目标或者背景杂波。在7.1章节中所描述的距离比率测试可以让我们摒弃掉背景杂波中产生的许多错误的匹配,但却不能移除来自其他正常物体的匹配,所以我们通常仍需要去判别在99%的外来特征中少于1%的内部特征的正确匹配子集。许多著名的拥有良好健壮性的方法,比如RANSAC或者平方最小中位数,在内部特征比例下降到明显低于50%时候,就表现得非常糟糕了。幸运的是,在空间形态上通过利用霍夫变换将特征集簇可以取得好得多的效果(Hough,1962;Ballard,1981;Grimson,1990)。
霍夫变换通过一致性描述来鉴别特征簇,它让每个特征对所有的物体形态进行选择,选出与该特征一致的物体。当发现特征的集簇选择了同一物体形态,这样的描述正确性概率就要比单个特征的高得多了。我们每一个关键点指定了4个参数,2D坐标、尺度和方向,库中每一个匹配关键点都有一套该关键点的参数记录用来与找到它的配准图像相联系。因此,我们可以创造一个霍夫变换去预测这个假设匹配的模型的坐标,方向和尺度。这样的预测有很大的错误隐患,因为通过这4个参数导出的相似变换对于3D物体形态空间全部的6个自由度只是一个近似,这还不包括任何的非刚性形变。因此,我们选用了这样的小的块,30度的方向,参数为2的尺度,0.25倍于最大配准图像尺寸(用预测尺度)的位置。为了在分块的任务中避免边界影响问题,每一个关键点的匹配在每一个维度都需要两个最接近的块,给予每一个假设和更高程度的形态扩展范围共计16个项。
在霍夫变换大多的运行过程中,都要用到一个多维数组来表示这些块。然而,许多潜在的块还是空的,并且由于他们相互的依存关系使得计算块的值的可能范围非常困难(例如,在所选的尺度离散化的位置依存关系)。我们可以通过使用块值的伪随机哈希函数来将选择插入一个单维哈希表来避免这些问题,这样很容易的避免冲突。
7.4 仿射参数的解决方案
霍夫变换用于鉴别所有至少包含有三个项的簇。每一个这样的集群都进行几何验证,用一个最小二乘方法来寻找最好的仿射投影参数,来将配准图像与新图像相联系。
一个仿射变换能正确地解答了在正投影下的平面3D旋转变化,但是对于空间物体的3D旋转效果却不好。而一个更加通用的解决方法是解决基本矩阵的问题(Luong 和Faugeras,1996;Hartley和Zisserman,2000)。然而,比起仅仅需要3个匹配点的仿射方法来说,基础矩阵的解决方案至少需要7个匹配点,而且在实际运用中还可能需要更多的匹配点来保持好的稳定性。我们希望通过仅仅3个匹配点来实现识别,所以仿射方案提供了一个更好的出发点,而且我们可以通过允许较多的残留错误来解决仿射近似中的错误问题。如果我们想象在物体周围套置一个球体,然后旋转圆球30度后,在球体内点的移动距离不会超过0.25倍的球体直径。比如在论文中引用的那个典型的三维物体,如果我们允许的残留误差能达到0.25倍的最大投影尺寸,那么仿射法将能很好的运行。还有一个更通用的方法(Brown 和Lowe,2002),这种方法的最开始也是基于相似变换,然后对于那些拥有丰富匹配的项再运用基础矩阵法深入解答。
一个模型点![]() 到一个图中点
到一个图中点![]() 的仿射变换可以写为:
的仿射变换可以写为:
其中模型转换矩阵是![]() ,仿射旋转、尺度和拉伸分别由这
,仿射旋转、尺度和拉伸分别由这![]() 个参数决定。
个参数决定。
我们希望找到这些转换参数,所以上面的方程可以被重写成如下的把未知参数集中在一个向量里的形式:
这个方程只是展示了一个简单的配准,更多深入的配准还可以被继续添加,每一个匹配都对第一个和最后一个矩阵添加了两个以上的行。此法需要至少3个的匹配才能运行。
我们能把这个线性系统表示为:
Ax=b
用最小二乘法求参数x,可以通过解这个与其相对应的标准方程,
![]() ,
,
使投影模型的位置到相应图像位置的距离的平方的和最小。这种最小二乘法也可以拓展到求解3D和铰接或柔性物体的参数的问题(Lowe,1991)。
通过检查每一个图像特征与其模型的一致性可以排除掉外来项的干扰。运用更加精确地最小二乘法,我们要求保证每个匹配的一致性,误差保持在在一半的范围内,以求得霍夫变换块的参数。 如果丢弃掉外来点后剩下的匹配点少于3个,那么就拒绝这个匹配。把外来点抛弃后,用剩下的点重新进行最小二乘,然后将此过程反复迭代。最后再补充进行一个从头至尾的匹配过程,来添加任何的能够与所建投影模型位置保持一致性的更深入的匹配。这些匹配可能是由于相似性转换的近似性或者其他错误而使得其在霍夫转换中被遗漏。
最后决定是否接受一个假设模型要基于之前论文所提到的一个详细的概率模型(Lowe,2001)。通过考虑到模型的投影大小、区域中特征点的个数和匹配的准确性,该方法首先计算了对模型形态错误匹配数量的期望值。贝叶斯分析给出了基于实际发现的特征匹配数量而使物体被呈现出来的可能性。如果正确匹配的最终概率大于0.98,我们将接受这个模型。对于图像中投影区域很小的对象来说,3个特征点就足以完成可靠的识别。 对于覆盖有深纹理图像的大的物体,错误匹配的期望数量会变高,这时大约就需要10个以上的匹配点了。
8.识别例子
图12.左侧显示了两个对象的训练图像。可以在杂乱的图像中识别出这些图像,并显示出广泛的遮挡。识别结果显示在右侧。在每个识别的对象周围绘制一个平行四边形,显示在识别期间解决的细微变换下原始训练图像的边界。较小的正方形表示用于识别的关键点。
图13.此示例显示了复杂场景中的位置识别。位置的训练图像显示在左上方,而从不同视点拍摄的640×315像素测试图像显示在右上方。识别出的区域显示在下部图像上,关键点显示为正方形,外部平行四边形显示用于识别的仿射变换下训练图像的边界。
图12显示了包含3D对象的杂波和遮挡图像的对象识别示例。左侧显示了玩具火车和青蛙的训练图像。中间图像(大小为600×480像素)包含隐藏在其他对象之后的对象实例,并且背景杂乱无章,因此即使对于人类视觉,也可能无法立即检测到这些对象。右图显示了最终正确的识别信息,叠加在图像的对比度降低的版本上。用于识别的关键点显示为带有额外线条的正方形,以指示方向。正方形的大小对应于用于构造描述符的图像区域。在每个识别实例周围还绘制了一个外部平行四边形,其侧面对应于在识别期间确定的最终仿射变换下投影的训练图像的边界。
该方法的另一个潜在应用是放置识别,其中移动设备或车辆可以通过识别熟悉的位置来识别其位置。图13给出了此应用程序的示例,其中在多个位置拍摄了训练图像。如左上方所示,这些物品甚至可以是看似没有区别的物品,例如木墙或带有垃圾桶的树木。右上方的测试图像(大小为640 x 315像素)是从相对于原始位置围绕场景旋转大约30度的视点拍摄的,但是易于识别训练图像的位置。
识别过程的所有步骤都可以有效实施,因此识别图2和3中的所有对象的总时间为。在2 GHz Pentium 4处理器上,12或13少于0.3秒。我们已经在装有摄像机的便携式计算机上实现了这些算法,并在各种条件下进行了广泛的测试。通常,可以在任何方向上,在几乎任何提供充足光线且不会产生过多眩光的照明条件下,在深度高达50度的旋转中可靠地识别带纹理的平面。对于3D对象,用于可靠识别的深度旋转范围在任何方向上仅约30度,并且照明变化更具破坏性。由于这些原因,最好通过集成来自多个视图的特征来进行3D对象识别,例如使用局部特征视图聚类(Lowe,2001)。
这些要点也已应用于机器人的定位和制图问题,其他论文对此进行了详细介绍(Se等,2001)。在此应用中,使用三目立体音响系统来确定关键点位置的3D估计。仅当关键点出现在所有3张图像中且具有一致的视差时,才使用关键点,从而导致异常值很少。随着机器人的移动,它会使用与现有3D地图的特征匹配对自身进行定位,然后在使用Kalman过滤器更新其3D位置的同时向地图上逐步添加特征。这为未知环境中的机器人本地化问题提供了可靠而准确的解决方案。这项工作还解决了位置识别的问题,在该问题中,可以打开机器人并在大地图内的任何位置识别机器人的位置(Se等,2002),这相当于对象识别的3D实现。
9.结论
由于其独特性,本文所述的SIFT关键点特别有用,这使得可以从其他关键点的大型数据库中选择关键点的正确匹配项。这种独特性是通过在图像的局部区域内组合代表图像梯度的高维向量来实现的。研究表明,关键点对于图像的旋转和缩放是不变的,并且在很大范围的细微畸变,噪声增加和照明变化方面都具有稳健性。可以从典型图像中提取大量关键点,从而在杂波中提取小物体时具有鲁棒性。在整个比例尺范围内都可以检测到关键点这一事实意味着,较小的局部特征可用于匹配较小且高度遮挡的对象,而较大的关键点在受噪声和模糊影响的图像上效果很好。它们的计算效率很高,因此可以在标准PC硬件上以接近实时的性能从典型图像中提取数千个关键点。
本文还介绍了使用关键点进行对象识别的方法。我们所描述的方法使用近似最近邻居查找,霍夫变换来识别在对象姿势,最小二乘姿势确定和最终验证上一致的聚类。其他潜在的应用包括用于3D重建,运动跟踪和分割,机器人定位,图像全景组装,对极校准的视图匹配,以及需要识别图像之间匹配位置的任何其他应用。
在推导不变和独特的图像特征方面,有许多进一步研究的方向。需要对具有完整3D视点和照明变化的数据集进行系统测试。本文描述的特征仅使用单色强度图像,因此可以通过包括照度不变的颜色描述符得出更多的区别(Funt和Finlayson,1995; Brown和Lowe,2002)。类似地,局部纹理量度似乎在人类视觉中起着重要作用,并且可以以比当前描述符所使用的单个空间频率更通用的形式并入特征描述符中。不变局部特征匹配方法的一个吸引人的方面是,无需选择一种特征类型,并且通过使用许多不同的特征可能会获得最佳结果,所有这些特征都可以提供有用的匹配并提高整体鲁棒性。
未来研究的另一个方向是单独学习适合识别特定对象类别的功能。这对于必须涵盖各种可能的外观的通用对象类尤其重要。Weber等人的研究。 (2000)和Fergus等。 (2003年)通过学习适合识别通用类对象的少量局部特征,展示了这种方法的潜力。从长远来看,特征集很可能既包含先验特征,又包含学习特征,这将根据可用于各种对象类别的训练数据量来使用。
致谢
我特别要感谢Matthew Brown,他建议对本文的内容和表示形式进行许多改进,并且他自己在特征本地化和不变性方面的工作为这种方法做出了贡献。此外,我还要感谢许多其他人的宝贵建议,包括Stephen Se,Jim Little,Krystian Mikolajczyk,Cordelia Schmid,Tony Lindeberg和Andrew Zisserman。这项研究得到了加拿大自然科学与工程研究委员会(NSERC)以及卓越中心机器人与智能系统研究所(IRIS)网络的支持。
参考文献
Arya, S. and Mount, D.M. 1993. Approximate nearest neighbor queries in fixed dimensions. In Fourth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA’93), pp. 271–280.
Arya, S., Mount, D.M., Netanyahu, N.S., Silverman, R., and Wu, A.Y. 1998.Anoptimal algorithm for approximate nearest neighbor searching. Journal of the ACM, 45:891–923.
Ballard, D.H. 1981. Generalizing the Hough transform to detect arbitrary patterns. Pattern Recognition, 13(2):111–122.
Basri, R. and Jacobs, D.W. 1997. Recognition using region correspondences. International Journal of Computer Vision, 25(2):145–166.
Baumberg, A. 2000. Reliable feature matching across widely separated views. In Conference on ComputerVision andPattern Recognition, Hilton Head, South Carolina, pp. 774–781.
Beis, J. and Lowe, D.G. 1997. Shape indexing using approximate nearest-neighbour search in high-dimensional spaces. In Conference on Computer Vision and Pattern Recognition, Puerto Rico, pp. 1000–1006.
Brown, M. and Lowe, D.G. 2002. Invariant features from interest point groups. In British Machine Vision Conference, Cardiff, Wales, pp. 656–665.
Carneiro, G. and Jepson, A.D. 2002. Phase-based local features. In European Conference on Computer Vision (ECCV), Copenhagen, Denmark, pp. 282–296.
Crowley, J.L. and Parker, A.C. 1984.Arepresentation for shape based on peaks and ridges in the difference of low-pass transform. IEEE Trans. on Pattern Analysis and Machine Intelligence, 6(2):156–170.
Edelman, S., Intrator, N., and Poggio, T. 1997. Complex cells and object recognition. Unpublished manuscript: http://kybele.psych.cornell.edu/∼edelman/archive.html
Fergus, R., Perona, P., and Zisserman, A. 2003. Object class recognition by unsupervised scale-invariant learning. In IEEE Conference on Computer Vision and Pattern Recognition, Madison, Wisconsin, pp. 264–271.
Friedman, J.H., Bentley, J.L., and Finkel, R.A. 1977. An algorithm for finding best matches in logarithmic expected time. ACMTransactions on Mathematical Software, 3(3):209–226.
Funt, B.V. and Finlayson, G.D. 1995. Color constant color indexing. IEEE Trans. on Pattern Analysis and Machine Intelligence, 17(5):522–529.
Grimson, E. 1990. Object Recognition by Computer: The Role of Geometric Constraints, The MIT Press: Cambridge, MA.
Harris, C. 1992. Geometry from visual motion. In Active Vision, A. Blake and A. Yuille (Eds.), MIT Press, pp. 263–284.
Harris, C. and Stephens, M. 1988.Acombined corner and edge detector. In Fourth Alvey Vision Conference, Manchester, UK, pp. 147–151.
Hartley, R. and Zisserman, A. 2000. Multiple view geometry in computer vision, Cambridge University Press: Cambridge, UK.
Hough, P.V.C. 1962. Method and means for recognizing complex patterns. U.S. Patent 3069654.
Koenderink, J.J. 1984. The structure of images. Biological Cybernetics, 50:363–396.
Lindeberg, T. 1993. Detecting salient blob-like image structures and their scales with a scale-space primal sketch: A method for focus-of-attention. International Journal of Computer Vision, 11(3):283–318.
Lindeberg, T. 1994. Scale-space theory: A basic tool for analysing structures at different scales. Journal of Applied Statistics, 21(2):224–270.
Lowe, D.G. 1991. Fitting parameterized three-dimensional models to images. IEEE Trans. on Pattern Analysis and Machine Intelligence, 13(5):441–450.
Lowe, D.G. 1999. Object recognition from local scale-invariant features. In International Conference on Computer Vision, Corfu, Greece, pp. 1150–1157.
Lowe, D.G. 2001. Local feature view clustering for 3D object recognition. IEEE Conference on Computer Vision and Pattern Recognition, Kauai, Hawaii, pp. 682–688.
Luong, Q.T. and Faugeras, O.D. 1996. The fundamental matrix: Theory, algorithms, and stability analysis. International Journal of Computer Vision, 17(1):43–76.
Matas, J., Chum, O., Urban, M., and Pajdla, T. 2002. Robust wide baseline stereo from maximally stable extremal regions.In British Machine Vision Conference, Cardiff, Wales, pp. 384–393.
Mikolajczyk, K. 2002. Detection of local features invariant to affine transformations, Ph.D. thesis, Institut National Polytechnique de Grenoble, France.
Mikolajczyk, K. and Schmid, C. 2002. An affine invariant interest point detector. In European Conference on Computer Vision (ECCV), Copenhagen, Denmark, pp. 128–142.
Mikolajczyk, K., Zisserman, A., and Schmid, C. 2003. Shape recognition with edge-based features. In Proceedings of the British Machine Vision Conference, Norwich, U.K.
Moravec, H. 1981. Rover visual obstacle avoidance. In International Joint Conference on Artificial Intelligence, Vancouver, Canada, pp. 785–790.
Nelson, R.C. and Selinger, A. 1998. Large-scale tests of a keyed, appearance-based 3-D object recognition system.Vision Research, 38(15):2469–2488.
Pope, A.R. and Lowe, D.G. 2000. Probabilistic models of appearance for 3-D object recognition. International Journal of Computer Vision, 40(2):149–167.
Pritchard, D. and Heidrich,W. 2003. Cloth motion capture. Computer Graphics Forum (Eurographics 2003), 22(3):263–271.
Schaffalitzky, F. and Zisserman, A. 2002. Multi-view matching for unordered image sets, or ‘How do I organize my holiday snaps?”’In European Conference on Computer Vision, Copenhagen, Denmark, pp. 414–431.
Schiele, B. and Crowley, J.L. 2000. Recognition without correspondence using multidimensional receptive field histograms. International Journal of Computer Vision, 36(1):31–50.
Schmid, C. and Mohr, R. 1997. Local grayvalue invariants for image retrieval. IEEE Trans. on Pattern Analysis and Machine Intelligence, 19(5):530–534.
Se, S., Lowe, D.G., and Little, J. 2001. Vision-based mobile robot localization and mapping using scale-invariant features. In International Conference on Robotics and Automation, Seoul, Korea, pp. 2051–2058.