【Paper Reading】FDML: A Collaborative Machine Learning Framework for Distributed Features
FDML: A Collaborative Machine Learning Framework for Distributed Features
原文来源:[Arxiv2019] FDML: A Collaborative Machine Learning Framework for Distributed Features
文章目录
- FDML: A Collaborative Machine Learning Framework for Distributed Features
-
- 1. Problem formulation
- 2. Asynchronous SGD for FDML
-
- 2.1 The Synchronous Algorithm
- 2.2 The Asynchronous Algorithm
- 3. Distribution Implementation
-
- 3.1 Implementation
- 3.2 Privacy
- 4. Experiments
- 5. Conclusion
欢迎大家访问我的GitHub博客
https://lunan0320.cn
1. Problem formulation
m 个不同的 parties,每个party有相同training samples
如图所示是n个samples
下图,代表了第i个sample的第j个party的features
下图代表第i个sample的所有features,是每个party的concatenation
p ( x , ξ ) p(x,\xi) p(x,ξ)是一个local model,输出是一个prediction
Feature Distributed Machine Learning (FDML) model:
(这里的 α j \alpha^j αj是一个sub-model,可以看作是一个local features 到 local prediction的映射)
( σ \sigma σ可以聚合local intermediate predictions, a j a_j aj是权重)
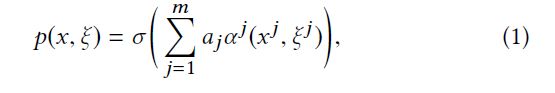
这里的model也是一个复合模型,每个sub-model都是可以不同的
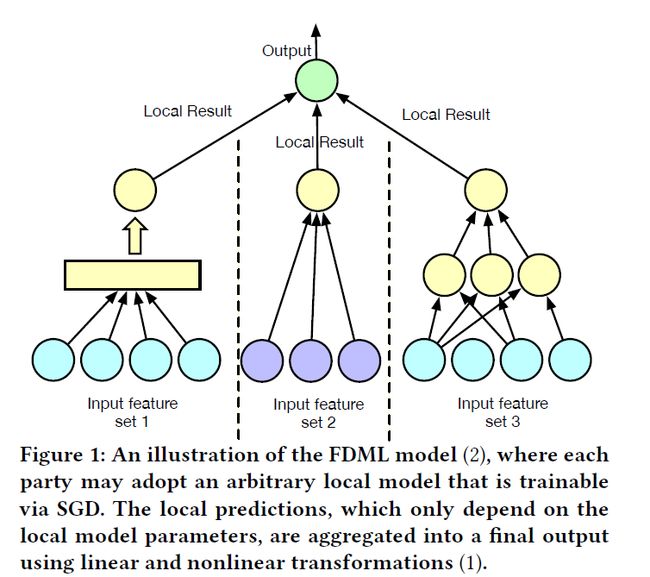
这里需要共享的只有 α j ( x j , ξ j ) \alpha^j(x^j,\xi^j) αj(xj,ξj),以此来得到final prediction
(raw data 和 sub-model parameters是不会泄露的)
目标函数:
L 是loss function, z ( x j ) z(x^j) z(xj)是sub-model x j x^j xj的正则项
2. Asynchronous SGD for FDML
i ( t ) i(t) i(t)是sample ξ i ( t ) \xi_{i(t)} ξi(t)在第 t iteration的 index
如下是在sample i ( t ) i(t) i(t),即 t iteration的objective function
整个training set的objective function:
(T是总的iteration number)
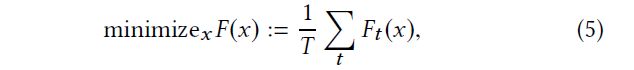
∇ F ( x ) ∈ R D \nabla F(x)\in R^D ∇F(x)∈RD是 F 的gradient, ∇ j F ( x ) ∈ R D j \nabla^jF(x)\in R^{D^j} ∇jF(x)∈RDj是 F对于sub-model 参数 x j x^j xj的partial gradient,即 ∇ j F ( x ) : = ∂ F ( x ) ∂ x j \nabla^jF(x):= \frac{\partial F(x)}{\partial x^j} ∇jF(x):=∂xj∂F(x),那么 ∇ F \nabla F ∇F就是所有的partial gradient 的concatenation
2.1 The Synchronous Algorithm
- 简单直接并行化SGD
第 t 个iteration,对于party j 的objective function的梯度:
这里用H来代表 ∑ k m α k ( x k , ξ i ( t ) k ) \sum_k^m\alpha^k(x^k,\xi_{i(t)}^{k}) ∑kmαk(xk,ξi(t)k)
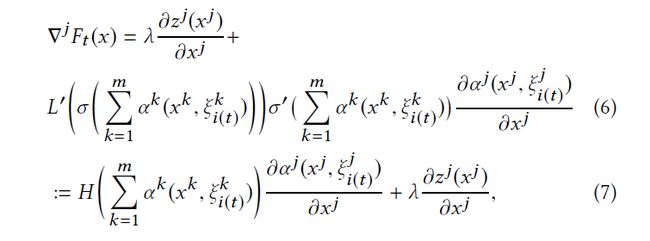
为了计算 ∇ j F \nabla^jF ∇jF,每个party只需要得到 ∑ k m α k ( x k , ξ i ( t ) k ) \sum_k^m\alpha^k(x^k,\xi_{i(t)}^{k}) ∑kmαk(xk,ξi(t)k),这就是在第 t 个iteration所有local prediction results 的聚合,剩余的项都可以用第 j 个party的local data计算得到。
2.2 The Asynchronous Algorithm
在异步情况下,每个party j 都会异步地更新自己的参数 x t j x_t^j xtj,任意的两个parties都可能是处于不同的iteration。
但是,这里假设不同的parties运行samples是go through in the same order
通常是随机生成sample index sequence,解决方案是:pseudo random number generator
local parameters update:
此时,很有可能 party 去quest local predictions 的 aggregation 时候,可能是 stale versions, x t − ι t j ( k ) x_{t-\iota_{t}^{j}(k)} xt−ιtj(k)
这里的 ι t j ( k ) \iota_{t}^{j}(k) ιtj(k),代表的是i从party j 到 party k 在 party j 的第 k 个 teration的 “ lag”
3. Distribution Implementation
3.1 Implementation
PS架构: workers 计算 gradients , server更新model
但是,在FDML中,server只要更新一个local prediction matrix A i , j A_{i,j} Ai,j (n行,m列)
用来hold 对于sample i 的最新的 m 个prediction
而且,worker在 FDML中是participating party,不仅需要计算 gradients,而且需要更新自己的 local model parameters
整个过程:
- a sample coordinator随机shuffle sample indices, 然后生成一个schedule i ( t ) i(t) i(t),每次都要找到 all features以及拥有sample对应的label。在算法开始之前每个party 就有: ξ i j , y i i = 1 n {{\xi_i^j,y_i}}_{i=1}^n ξij,yii=1n
- 每个party update 自己对sample i ( t ) i(t) i(t) 的 local prediction A i ( t ) , j A_{i(t),j} Ai(t),j

(Push request: 即 worker j 在iteration t,upload value c)
- party Pull 最新的的 ∑ k = 1 m A i ( t ) , k \sum_{k=1}^{m}A_{i(t),k} ∑k=1mAi(t),k
- party update x t j x_{t}^j xtj 到 x t + 1 j x_{t+1}^j xt+1j
a fully synchronous algorithm可以在最短的iterations 达到converge
但是,导致了更大的等待同步的时间
a asynchronous algorithm可以减少每轮的时间,但是需要更多的iterations达到converge
为了减少总的时间,需要最快iteration的party比最慢的iteration超出的不能超过bound ι \iota ι (加入bound 来保证 convergence)
SGD algorithm可以被更好的 mini-batch SGD替换

3.2 Privacy
不会泄露 weights 和 features 信息
共享的信息只是:local prediction (是对于 local weights 和 local features 的复合函数)
此外,也可加入扰动项,noise 对于local prediction
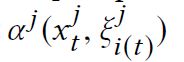
4. Experiments
an app recommendation task at Tencent MyApp
利用另外两个app中的信息达到 cross-domain的效果,提高准确性
Dataset:
- Tencent MyApp data : 5, 000, 000 labeled samples indicating whether a user will download an app or not
- a9a,: classical census dataset, where the prediction task is to determine whether a person makes over $50K a year.
Model:
-
logistic regression (LR)
-
a two layered fully connected neural network (NN)
Training schemes:
- Local: 7, 000 local feature or 67 features of a9a
- Centralized: collect all the 8, 700 features or using all the 124 features in a9a
- FDML: 8, 700 features distributed or a9a classification model on all 124 features from two different parties
如下Tables, FDML在保证local features的同时,优于 Local scheme,接近于Centralized的情况
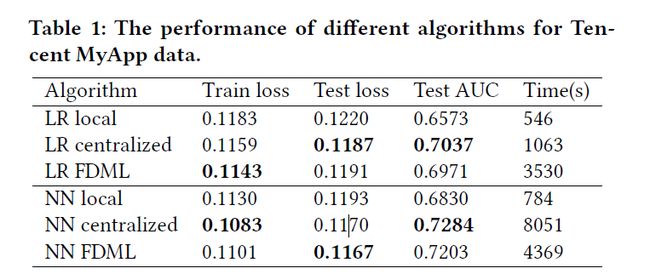
LR model:objective value,loss , AUC值 FDML与Centralized情况下都比较好
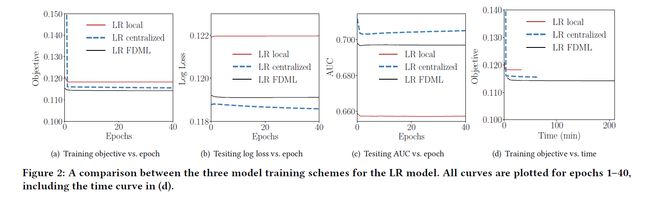
NN model: 两种机制下,local scheme都是最快的,没有communication 和 synchronous 的开销

DP 机制: 不同的noise level
5. Conclusion
motivation: 相同的 training sample 在不同的app 中有不同的features,但是一个app中的data必须对其他的app是confidential
convergence:达到与目前最快的data-parallel SGD in a stale synchronous parallel , O ( 1 / T ) O(1/\sqrt T) O(1/T), T是iteration number
results : FDML AUC、loss 效果接近于centralized training (后者model更复杂)
future work: add momentum and privacy