【Paper Reading】VAFL: a Method of Vertical Asynchronous Federated Learning
VAFL: a Method of Vertical Asynchronous Federated Learning
原文来源：[Arxiv2020] VAFL: a Method of Vertical Asynchronous Federated Learning
文章目录
- VAFL: a Method of Vertical Asynchronous Federated Learning
-
- 0. Abstract
- 1. Introduction
-
- 1.1 Prior part
-
- Federated Learning
- Privacy-preserving learning
- Asynchronous and parallel optimization
- 1.2 This work
- 2. Vertical federated learning
-
- 2.1 Problem statement
- 2.2 Asynchronous client updates
- 2.3 Types of flexible update rules
- 3. Convergence analysis
-
-
- Assumption 1
- Assumption 2
- Assumption 3
- 3.1 Convergence under bounded delay
-
- Assumption 4 (Uniformly bounded delay)
- Theorem 1
- Theorem 2
- 3.2 Convergence under stochastic unbounded delay
-
- Assumption 5 (Stochastic unbounded delay)
- Theorem 3
- Theorem 4
-
- 4. Perturbed local embedding: Enforcing differential privacy and smoothness
-
- 4.1 Local Perturbation
- 4.2 Enforcing smoothness
-
- Theorem 5
- 4.3. Enforcing differential privacy
-
- Theorem 6
- 5. Numerical tests and remarks
-
- 5.1 VAFL for federated logistic regression
- 5.2 VAFL for federated deep learning
欢迎大家访问我的GitHub博客
https://lunan0320.cn
0. Abstract
-
Horizontal Federated learning (HFL) ：多个client data之间共享相同的特征
-
vertical FL： 从不同的clients之间联合所有的features（两个数据集共享相同样本空间，但是特征空间不同）
VAFL: 每个client 在不需要于其他clients协商的情况下，运行随机梯度下降
new technique： Perturbed local embedding 来保护数据隐私和提高通信效率。
-
理论分析: strongly convex, nonconvex, nonsmooth objectives
-
实验验证：应用于各类图像和健康数据集
Result : 比较了中心化方法centralized 以及 同步 synchronous FL方法
1. Introduction
Federated Learning ：一个central server和多个clients协同训练一个机器学习模型
与已经存在的分布式机器学习范式相比，FL增加了同步clients、数据模型隐私保护的困难性
大多数已经存在的FL方法考虑的场景是HFL，即clients有一个不同的数据集，他们共享相同的特征
Horizontal FL: 可以协同训练从feature space 到 label space
相同的samples，每个client有独一无二的features
应用场景：电子商务、金融、健康医疗等
（电子商务公司从多个金融机构使用用户的交易来预测用户的信用）
（医疗机构使用一个病人在不同医院的临床诊疗数据来评估病人的健康水平）
场景中，数据拥有者有相同用户的不同的records。通过联合他们的特征，可以建立一个更加准确的模型——这就是feature-partitioned or vertical FL
-
HFL： 全局模型在一个server处完成对local model的聚合，local model是被每个client在本地使用local data更新完的
-
VFL: global model是local models的 concatenation，这是与loss function成对出现的。因此，更新一个client的local model是需要其他的clients的信息的。
这种强的模型依赖性，导致了在隐私保护以及通信效率方面的挑战。
1.1 Prior part
Federated Learning
HFL: large data 中划分给all clients, share the same feature space
communication efficiency是一大问题：
1）减少number of bits per communication round
2）节省number of communication rounds
Privacy-preserving learning
不同于在HFL中聚合梯度，在VFL中的 local gradients可能会involve raw data of other clients
Differentiable privacy：
1）是一种可量化的隐私措施
2）许多已经存在的学习算法通过简单调整可以实现DP
但是并不是为VFL而设计的
Asynchronous and parallel optimization
asynchronous 和 parallel优化方法是通常被用来解决asynchrony和delay的问题
对于feature-partitioned vertical FL，尤其与Block Coordinate Descent (BCD )方法有关
异步的BCD和随机变量已经应用于bounded delay
最新算法可以考虑unbounded delay在blockwise或者stochastic update的情况
最新的异步方法不能保证:
1）loss function在nonsmooth情况下的收敛性
2）local update的privacy
1.2 This work
-
A general optimization formulation
VFL包括一个global model和对于每个client的一个local embedding model
local embedding model(linear, nonlinear, nonsmooth) 可以将raw data 映射为紧凑的特征，从而减少与global model 通信的次数
-
Flexible federated learning algorithms
client间歇性的参与，非协同训练，以及DP、MPC
-
Rigorous convergence analysis
建立性能的下界和隐私的保护水平
2. Vertical federated learning
2.1 Problem statement
M个clients，N个samples，每个client与一个unique set的features相关
x n , m x_{n,m} xn,m
是第n个sample vector的第m个block
y n y_n yn
是第n个sample对应的label，存储在server中
每个client上的特征集是不同的，在第m个client上保存的特征 x n , m ∈ R p m x_{n,m}\in R^{pm} xn,m∈Rpm，Pm表示第m个client上数据的维度
每个client在本地learns 一个 local（linear or nonlinear）embedding function h m h_m hm, 把较高维度的x_n,m映射到一个低维度，即数据维度pm映射到公共维度 p ‾ m \overline pm pm
目标函数：
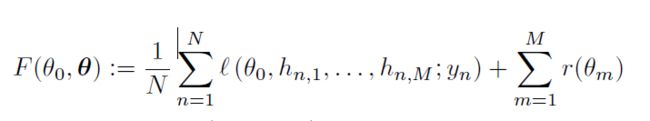$$ \theta_0是server的global\quad model的参数，\bold{\theta}是local\quad clients参数的串联\\ l是loss function,r是正则项 $$ client m的本地信息是embedding vector $h_n,m$
整个过程中传输的参数为： h n , m {h_{n,m}} hn,m 和 梯度
∇ h n , m l o s s \nabla h_{n,m}loss ∇hn,mloss
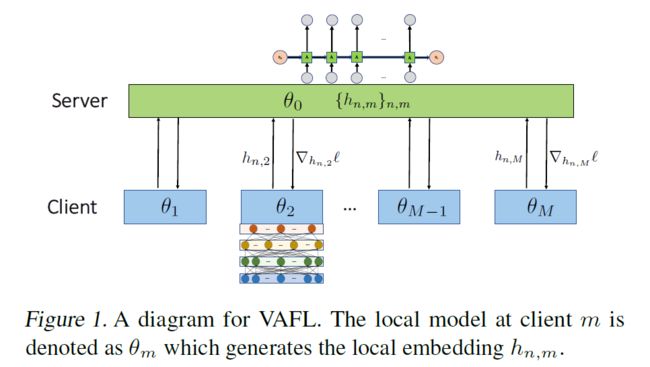
2.2 Asynchronous client updates
server接收来自active client m的：
1）a query：关于loss function的 gradient
2）a new embedding vector h n , m h_n,m hn,m : 使用更新的local model的参数来计算
对于query 1），server 使用当前的 {h_n,m} 为client m计算gradient
对于query 2），server计算新的梯度，使用当前收到的clients的updates，来更新global model的参数 θ 0 \theta_0 θ0
一次interaction：
client: active client m 随机选择data x n , m x_n,m xn,m，并向server query对应的梯度，之后上传更新后的embedding vector h n , m h_n,m hn,m，然后更新本地的参数 θ m \theta_m θm
server: 收到embedding vector h n , m h_n,m hn,m，计算gradient，更新server的参数 θ 0 \theta_0 θ0
k代表global counter or iteration
在第k个sample上随机梯度的 loss值:
1）server model
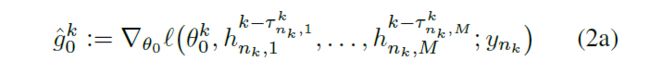
2）local model
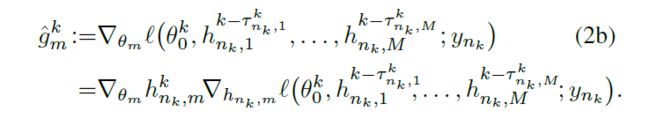
delay的定义:
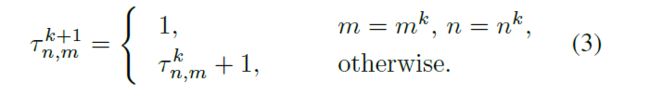
- server端的更新：
- activate local client端的更新：
- other clients的更新：
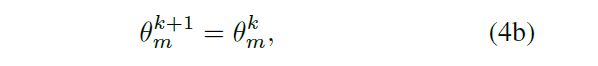
2.3 Types of flexible update rules
延迟delay是存在的，来自于异步通信和随机sampling
为了确保收敛，对于灵活更新协议上的设置：
- Uniformly bounded delay D.
在训练过程中，delay如果超过了D，server就会立刻重新query fresh的 h n , m h_n,m hn,m
- Stochastic unbounded delay.
每个client的activation是一个随机的过程，delay取决于随机过程的hitting times
因此，如果activation服从一个独立的Poison processes，delay就会服geometrically distributed
- t-synchronous update, t > 0.
全异步的update是most flexible，但是t-synchronous update也是通常采用的
sever直到收到t个client的 h n , m h_n,m hn,m才计算gradient，然后去更新server的model
实验表面，t-synchronous具有更加稳定的性能。
3. Convergence analysis
在nonconvex 和 strongly convex情况下展现收敛性情况
如下展示 fully synchronous version of VAFL 的收敛率
首先，是对sampling 和 smoothness的一些假设：
Assumption 1
（1）Sample index {n_k}是 i.i.d
（2）gradient的variance服从如下：
E [ ∣ ∣ g m k − ∇ θ m F ( θ 0 k , θ k ) ∣ ∣ 2 ] ≤ σ m 2 , g m k 是 在 没 有 d e l a y 下 的 g m k ^ E[||g_m^k - \nabla\theta_mF(\theta_0^k,\theta^k)||^2 ] \le\sigma_m^2,\quad g_m^k是在没有delay下的\hat{g_m^k} E[∣∣gmk−∇θmF(θ0k,θk)∣∣2]≤σm2,gmk是在没有delay下的gmk^
Assumption 2
optimal loss 是 有下界的
F ∗ > − ∞ ， ∇ F 是 L − L i p s c h i t z c o n t i n u o u s F^* > -∞，\nabla F是 L-Lipschitz\quad continuous F∗>−∞，∇F是L−Lipschitzcontinuous
Assumption 2 在 nonsmooth local embedding 函数下通常是无法满足的 (neural networks)
对此，使用 perturbed local embedding 可以增加smoothness
Assumption 3
activation of all clients满足 independent Poisson process
3.1 Convergence under bounded delay
Assumption 4 (Uniformly bounded delay)
在第k个iteration，delay是有界的
The convergence for the nonconvex case
Theorem 1
学习率满足
则有
在强convexity 的情况下，convergence rate得到提升
Theorem 2
额外的假设 F 是 u-strongly convex，第k轮的学习率满足：
则有：
3.2 Convergence under stochastic unbounded delay
Assumption 5 (Stochastic unbounded delay)
对于每个client m，delay是随机的无界的
Theorem 3
学习率满足
则有
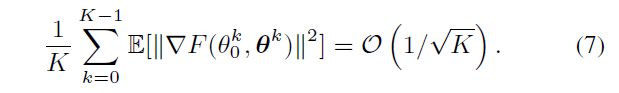
Theorem 4
假设 F 是 u-strongly convex，学习率满足：
则有
在有界和无界假设的情况下，但随机延迟的假设下，算法都能达到收敛
4. Perturbed local embedding: Enforcing differential privacy and smoothness
介绍一个 local perturbation technique,促进DP和smooth
4.1 Local Perturbation
h m h_m hm 是一个linear embedding时，可以看作：
$h_m $是一个nonlinear embedding时，例如 neural networks，可以看作：
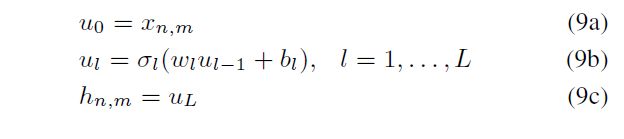
perturbe 过程：
在每个layer，加入一个random neuron的output Z l Z_l Zl来perturb local embedding function
perturbation distribution满足：
11a 是均值为0，方差为c 方的Gaussian distribution
11b 是uniform distribution
4.2 Enforcing smoothness
受到randomized smoothing启发，因此对random neuron的期望值，可以smooth objective function
通过适当的方式卷积，可以提高function的smoothness
通过增加random neuron Z_l, σ l \sigma_l σl将会被smoothed
通过进一步诱导，可以证明loss function 对local embedding vector h_m的平滑性
Theorem 5
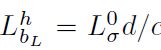
local model 的 smoothness constants满足：
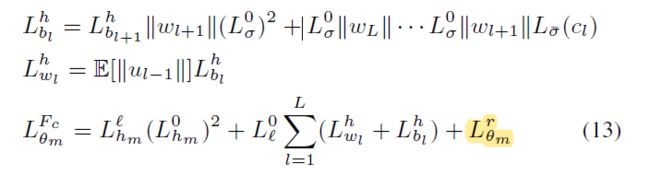$$ L_{\theta m}^{F_c} 是正则项的smoothness\quad constant\\ L_{bl}^{h}和L_wl^h是perturbed\quad local\quad embedding h \\的smoothness\quad constant $$ 
是均匀扰动下的第l层neuron的smoothness constant
对于local model来说，perturbed loss 是smooth，大的扰动（更大的c）会导致更小的平滑常数
4.3. Enforcing differential privacy
将perturbed local embedding technique与private information exchange联系
a trade-off between privacy and accuracy
Gaussian differential privacy (GDP)
u-GDP ：两个neighboring 数据集 S 和 S’ 满足：
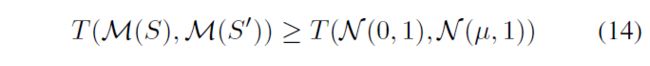
u越小，privacy loss越少
Theorem 6
设置在第L 层的Gaussian random neuron的variance为：
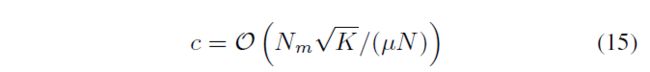
VAFL对于client m满足 u-GDP
为了提高privacy,可以decrease u，增加 random neurons 的 variance
但是在增大 variance of random neurons的同时，stochastic gradient也是在增加，可能会导致收敛效果变差
5. Numerical tests and remarks
测试
(1) fully asynchronous version VAFL (async)
(2) t-synchronous version VAFL (t- sync)
(3) private version via perturbed local embedding technique
5.1 VAFL for federated logistic regression
在MNIST、Fashion-MNIST、CIFAR 10 以及 Parkinson disease datasets上进行logistic regression
下面的图片依次是在这四个数据集上的ACC
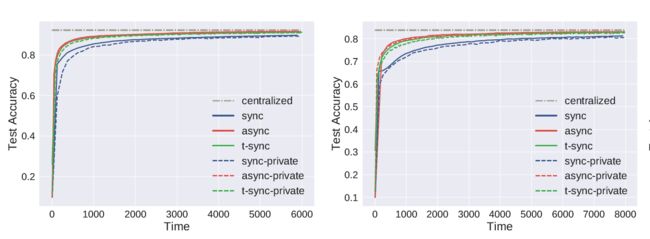
5.2 VAFL for federated deep learning
neural network是从MVCNN修改得到
client：使用7-layer CNN作为local embedding function
server：使用fully connected network来聚合local embedding vectors
测试在MIMIC-III数据集上VAFL的准确性（死亡率预测）
每个client使用LSTM作为embedding function
