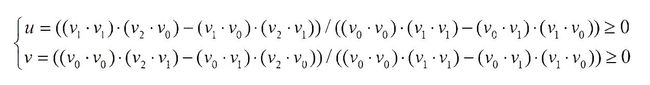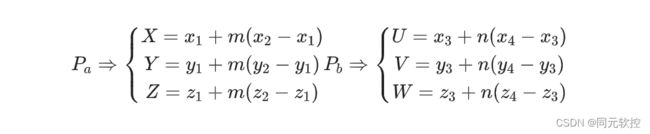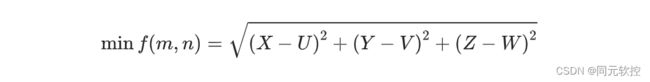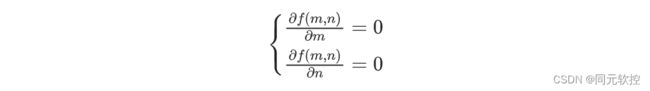技术干货|赌神摇骰子——基于MWORKS/Modelica的刚体动力学接触建模与仿真
发哥摇骰子的这个名场面想必大家都不陌生吧,今天我们就借着摇骰子这个名场面向大家分享一些多体接触模型开发的建模机理和思路。
摇骰子是多个物体之间相互碰撞接触的物理过程。从机理角度看,该过程涉及多体动力学、接触动力学及几何图形学。摇骰子动力学模型可基于MWORKS.Sysplorer软件,借助Modelica多体库构建。本篇文章关注的是如何应用接触动力学及几何图形学理论模拟摇骰子接触碰撞的物理过程。
1 基本概念描述
1.1 接触动力学实现机理
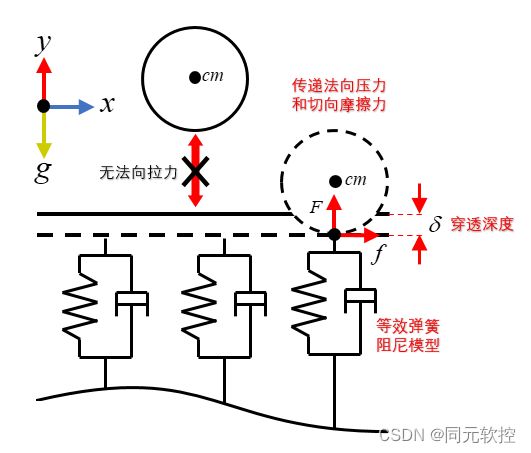
通常刚体间发生接触碰撞必然满足以下三个条件:
- 刚体之间不产生明显穿透;
- 刚体之间能够传递法向压力和切向摩擦力;
- 刚体之间不传递法向拉力。
当刚体间发生接触时,其间的接触力采用弹簧阻尼模型进行计算,该值与刚体间的穿透深度(产生刚力)和穿透速度(产生阻尼力)有关。
图1 二维点面接触等效示意图
1.2 几何图形学
几何图形,即从实物中抽象出的各种图形,可帮助人们有效的刻画错综复杂的世界。生活中到处都有几何图形,我们所看见的一切都是由点、线、面等基本几何图形组成的,所以几何模型间的接触问题实际上就是点、线、面三类几何元素之间的接触问题。我们可以通过这些几何元素的代数方程进行接触判断和处理。
图2 几何图形
2 模型构建
2.1 建模思路
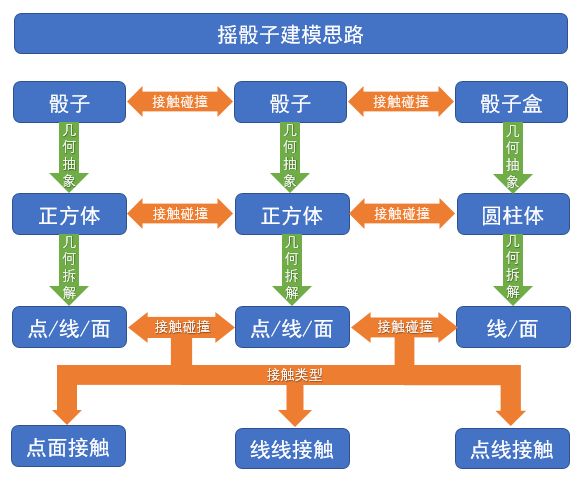
回到摇骰子的问题上来,摇骰子需要用到骰子盒和骰子。根据几何图形学思想,我们可以将骰子盒、骰子抽象为圆柱体、正方体几何图形。
图3 几何模型简化示意图
这样一来,摇骰子的接触碰撞问题就可以转换为圆柱体与正方体,正方体与正方体之间的接触碰撞问题了。本文摇骰子的建模思路具体如下:
图4 摇骰子建模思路
2.2 骰子与骰子的接触
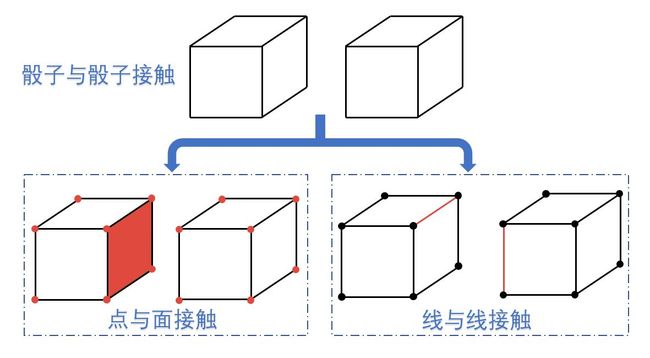
从示意图上可看出骰子与骰子的接触主要涉及到点面接触和线线接触。
图5 正方体几何元素接触类型
2.1.1 点面接触
在这里,主要通过点面接触模型来向大家详细介绍接触模型算法的本质。
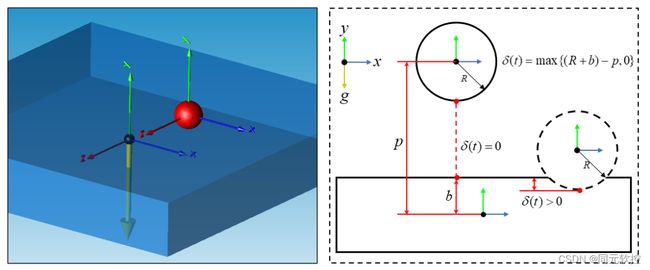
图6 点面接触二维示意图
从示意图上可知,当球与面的距离小于0时,也就是两刚体发生穿透时即判定为发生接触。这里我们用穿透深度δ(t)=max{(R+b)-p(t),0}来表征两刚体间的穿透程度,当δ(t)>0时判定发生接触,其值越大穿透现象越明显,从而产生的相互作用力也就越大。当刚体发生接触时,刚体之间接触产生的法向压力我们采用弹簧阻尼模型进行等效,其值与穿透深度δ(t)和面法向相对速度VV(t)有关。具体表达式如下:
接触弹力:
接触阻尼:
刚体间接触产生的摩擦力f可以根据库伦定律结合三次阶跃函数计算,其值与接触弹力F和切向相对速度Vt(t)有关。具体表达式如下:
摩擦力:
最终接触弹力F和摩擦力f的矢量和就是刚体间的相互作用力。
表1 接触及摩擦力参数定义
| 定义 | 描述 |
| n | 非线性指数 |
| δm | 求解的ODE问题穿透深度阈值 |
| K | 接触刚度 |
| Cm | 接触阻尼 |
| Vs | 最大静摩擦对应的滑移速度 |
| Cst | 静摩擦系数 |
| Vtr | 动摩擦对应的相对滑移速度 |
| Cdy | 动摩擦系数 |
根据上述公式,我们可以发现,相互作用力的值只与刚体间的速度矢量V(t)和穿透深度δ(t)有关。其中,速度矢量V(t)可以借助Modelica多体库很方便的获取,而我们只需要计算穿透深度值δ(t)即可。所以,接触算法的实质其实就是求穿透深度δ(t)的过程。
2.2.2 区域判断问题
接触算法代码虽然实现了,但是只适用于解决点与无限平面的接触问题,而实际我们要处理的是点与有限区域的面接触过程。所以判断接触点何时处于接触面区域内是开发几何体接触模型的前提。
图7 区域判断示意图
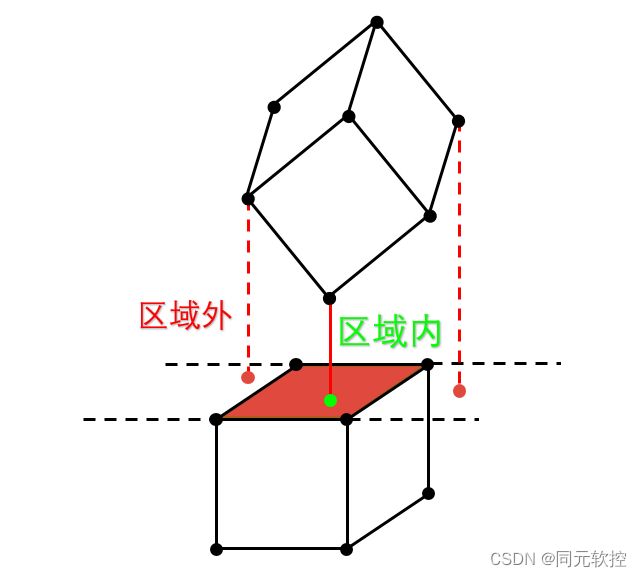
实际上任何一种多边形或曲面都可以用若干个三边形面拼接而成。因此只要解决点与三边形面区域判断问题,那么复杂几何体的区域判断问题也就迎刃而解,这里我们结合如下示意图,采用重心法来判断点是否在三边形面区域内。
图8 点与三边形区域判断示意图
点与三边形面区域判断算法:
当u,v≥0时接触点处于三边形面区域内,然后进行接触算法计算,否则不进行接触计算。对于点与矩形面区域的判断,这里将矩形面拆分成两个三边形面即可实现。
好了,点与面的接触算法就这样解决了,至于多点对多面这一情况,可以应用多体动力学理论进行实现,这里就不向大家啰嗦了。
在这里举一个四足机器人的应用案例向大家展示下点面接触的应用效果。
图9 点面接触应用案例
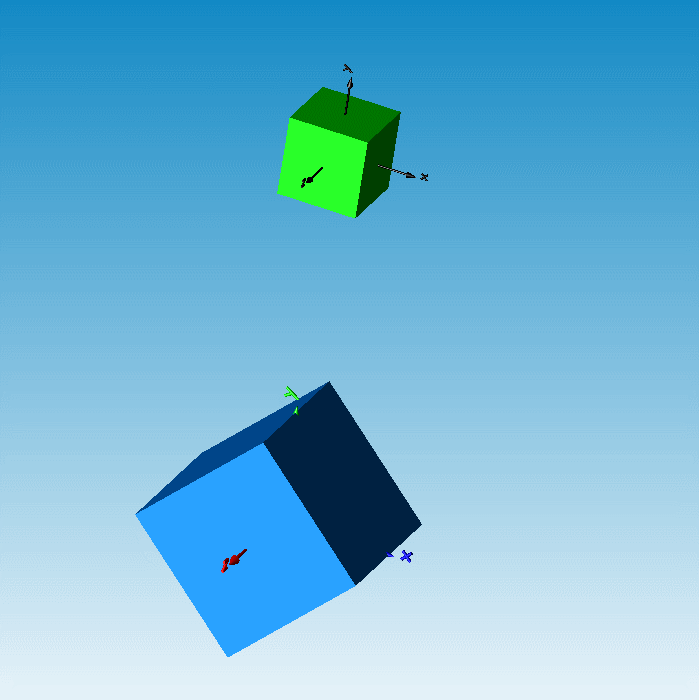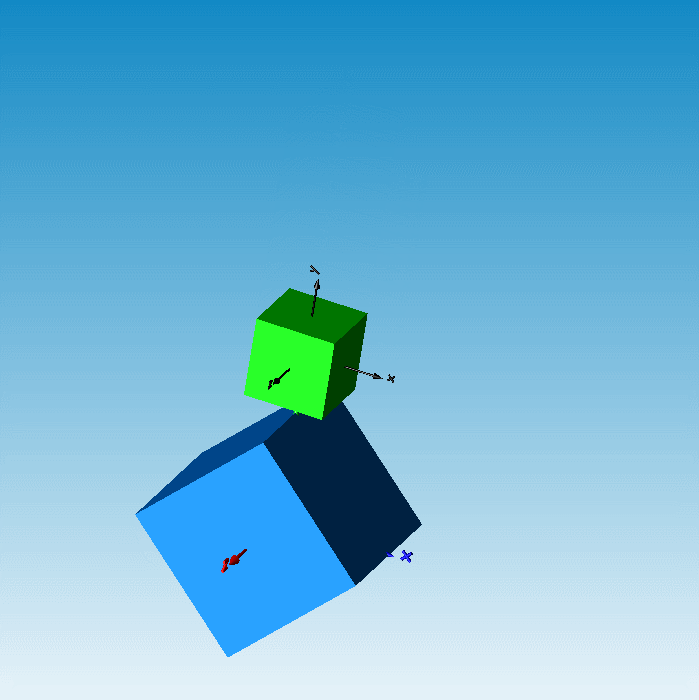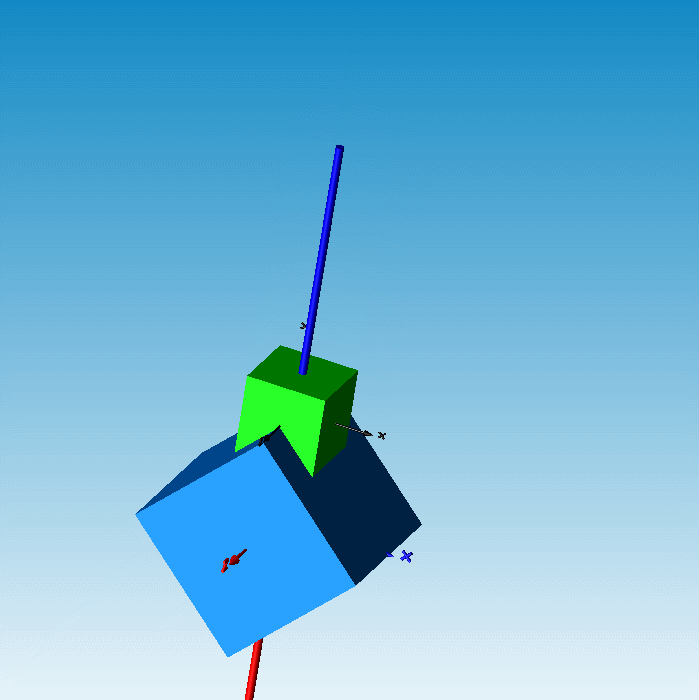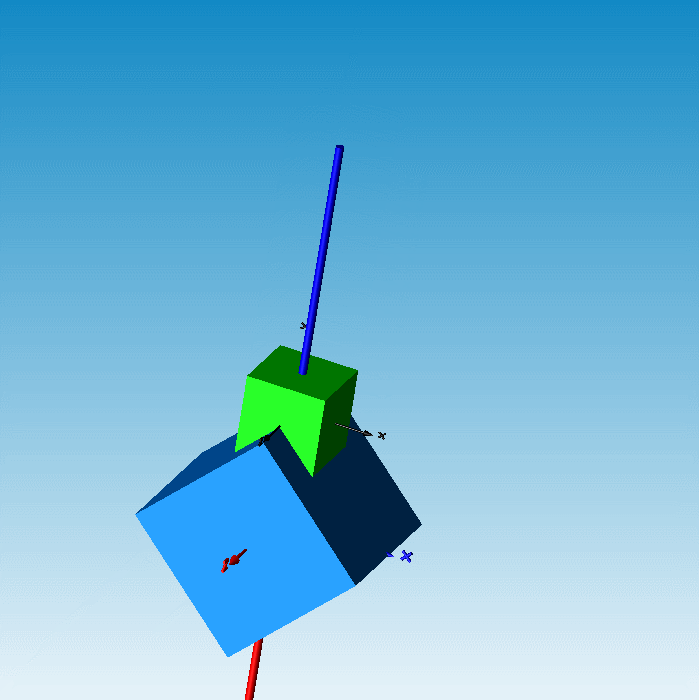
点面接触算法虽实现了,但正方体与正方体接触时只用到点面接触的话会出现下图所示的干涉问题。要想避免此现象,还需在几何体上选取无数个点单元进行与面的接触计算,但是几何点单元的数量会直接影响模型的求解效率和求解精度。故而在考虑求解效率和求解精度的前提下,我们选择对模型增加线线接触功能来避免所述干涉现象。
图10 正方体间存在的干涉现象
2.2.3 线线接触
关于线线接触模型,需要考虑两种情况:一是线段共面时的接触,另一种是不共面的情况。第一种情况我们可以通过点线接触的思路去实现(具体可参考本文2.2.1节内容)。
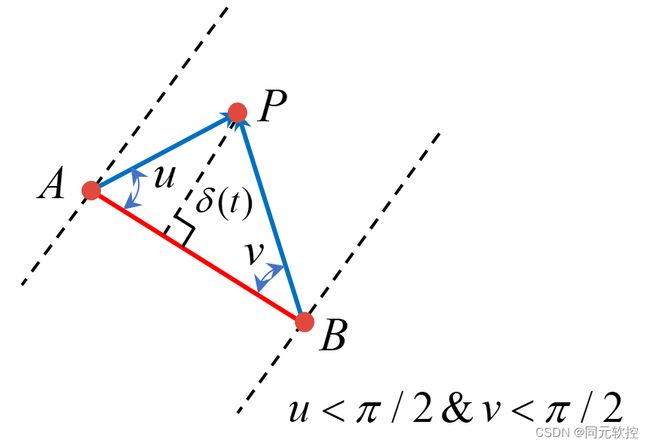
对于非共面线段,线段与线段的接触点是时刻变化的,那我们该如何去计算各个时刻接触点的位置信息呢?这里我们用到了公垂线理论,我们知道两条非共面的直线,有且仅存在一条直线使得其与两条直线均垂直,而两条线段发生接触时的接触点一定是公垂线与线段的交点,因此我们只要求出公垂线矢量信息,即可获取各个时刻下接触点之间的距离值,从而就可求出穿透深度δ(t)。
我们假设空间中有两条线段AB和CD,如上图所示,Pa和Pb分别为线段AB和CD与公垂线的交点,那么Pa和Pb的坐标值可以用以下方程描述。
当0≤m,n≤1时说明Pa和Pb点在线段AB和CD上。否则就是各自在线段延长线上的点。知道Pa和Pb的表达式后我们就可以求出两点之间的距离为:
求两线段的公垂线也就等效为求PaPb的最小值问题。
然后对函数f(m,n)求关于m,n的偏导,即可得到一个二元一次方程组:
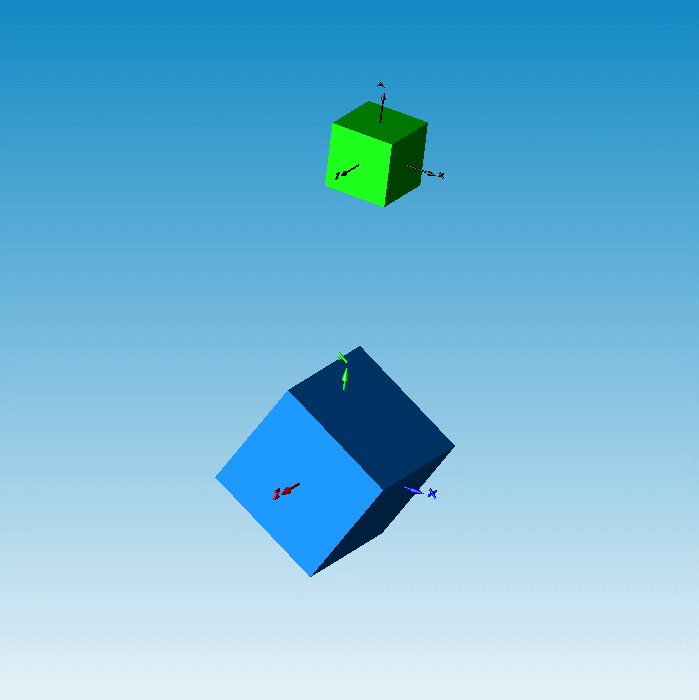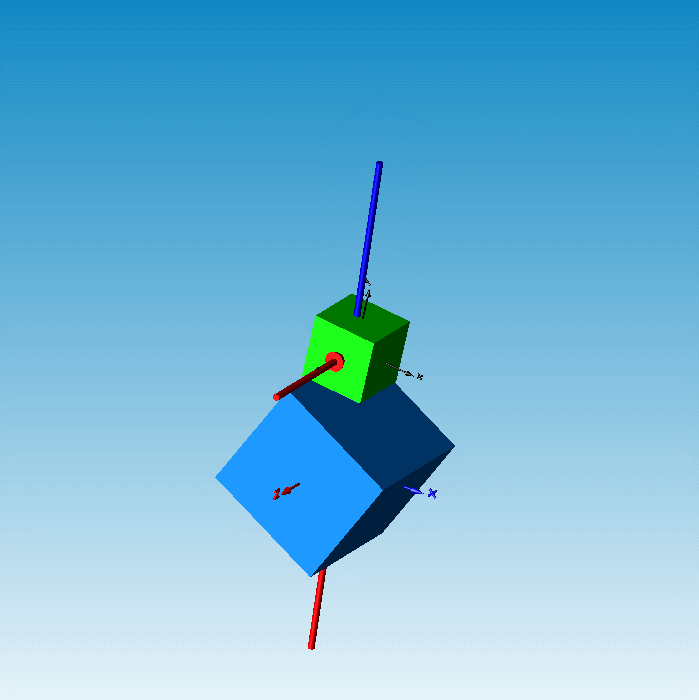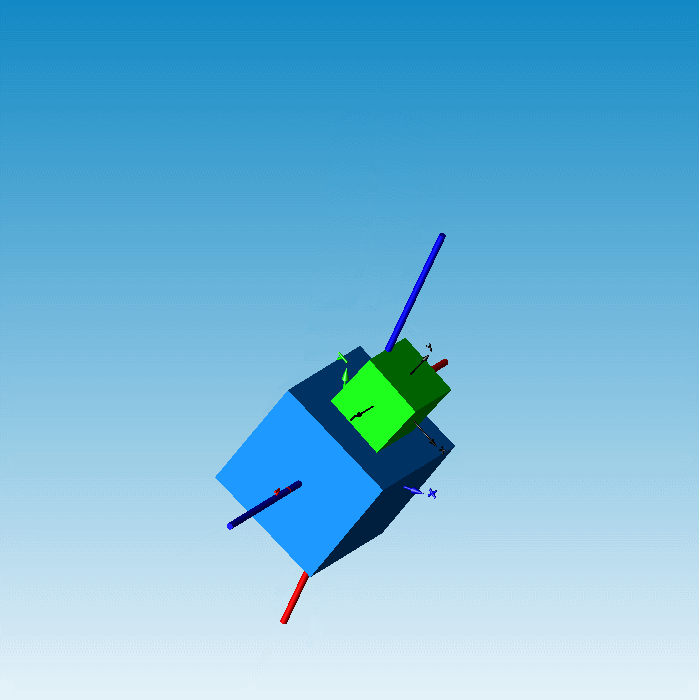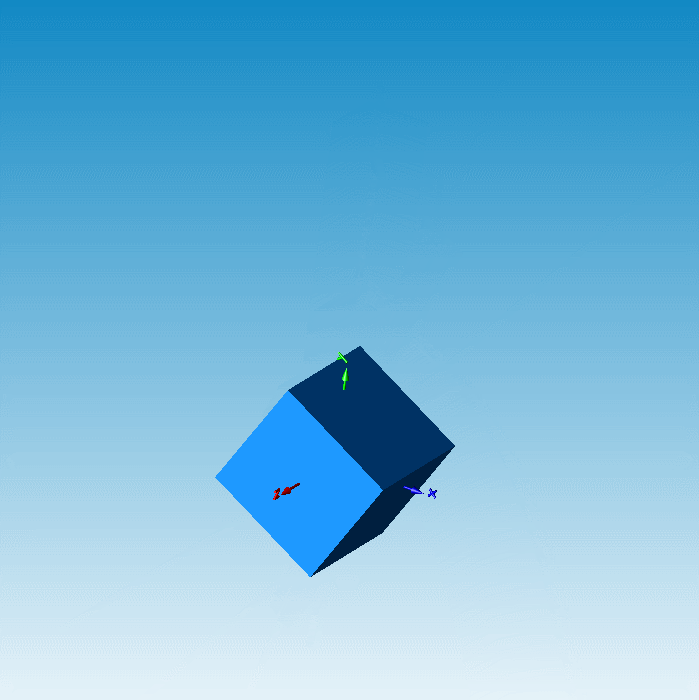
根据上述方程组即可求出m,n的值,从而可确定接触点之间的距离以及接触点位置矢量。根据这两个信息我们就可以套用接触算法公式来实现线线接触模型的开发了。在应用线线接触模型后的立方体接触仿真结果就不会出现上述的干涉问题了。
图12 应用线线接触后的应用效果
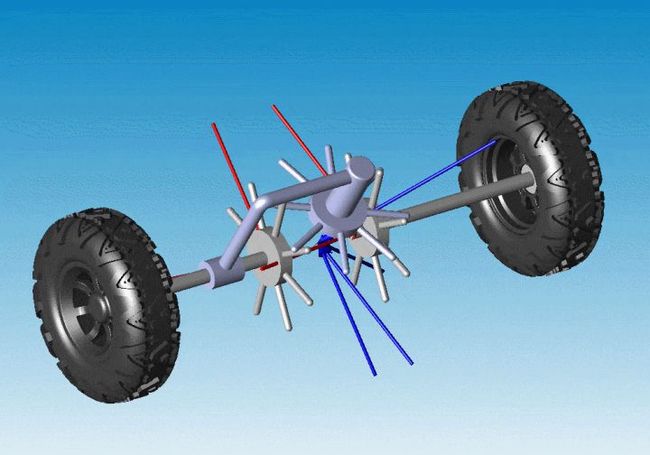
接下来我们再举一个汽车差速器经典教学案例来向大家展示下线线接触模型的应用效果。
图13 汽车差速器经典教学案例
以下是我们使用线线接触模型实现的效果。起初对两车轮施加同样的阻力矩,之后增大左车轮的阻力矩,此时的效果就和案例中的一致了。
图14 线线接触在差速器上的应用效果
图中单箭头是相互作用的力矢量,双箭头是相互作用的力矩矢量。
2.3 骰子与骰子盒的接触
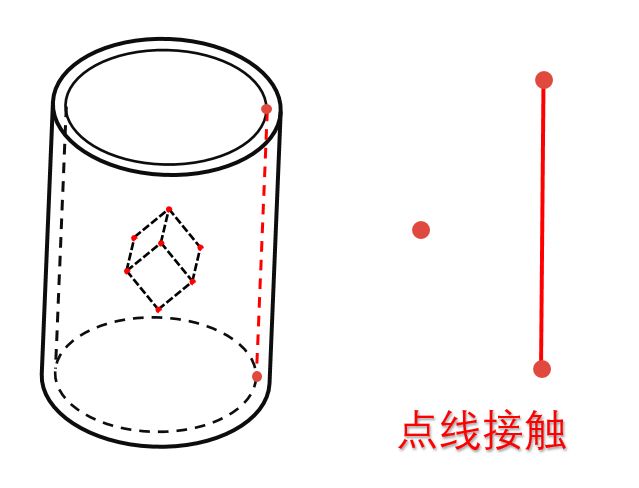
对于骰子与骰子盒的接触问题,我们将骰子盒抽象为圆柱体,然后把正方体与圆柱内面的接触转化为正方体的八个点元素与圆柱体中的无数根线段元素的接触过程。因此解决点与线段的接触问题是解决骰子在骰子盒内面的接触碰撞问题的前提。
图15 骰子与骰子盒接触等效示意图
2.2.1 点线接触
点与线接触主要涉及两个问题,一是点到直线距离的计算,另一个是点何时处于线段区域内。下图给出了点线区域判断的解决思路,比较简单,这里就不赘述了。
接下来就是判断几何点将要与圆柱面的哪根线段接触?这里大家可根据如下示意图进行理解。也就是根据当前点元素相对圆柱几何体坐标系的位置向量,结合圆柱半径求出线段元素端点相对圆柱几何坐标系的位置向量,这样我们就可以实时获取点元素即将要与哪条线段接触的空间几何信息。
图17 接触线段几何信息示意图
解决以上问题后,来看下实际的一个应用效果如何:
图18 点与圆柱接触应用案例
3 仿真模拟
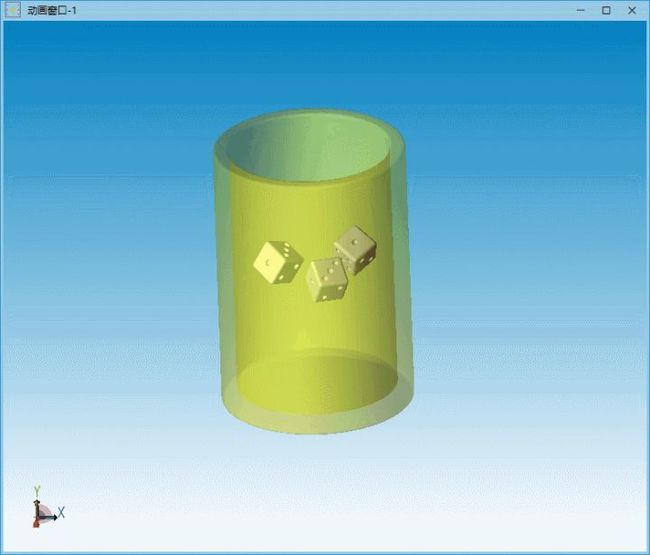
到此为止摇骰子所用到的接触模型基本已开发完成,接下来看看实际的应用效果吧。
图19 摇骰子仿真模拟
4 总结
摇骰子动力学仿真案例基本上涵盖了所有用到的接触类型,如点面接触,点线接触以及线线接触。实际上再复杂的几何体接触也都离不开这三种接触类型。以这三种接触类型为基础还可以扩展更多有意义的刚体动力学接触场景。比如本文还利用点线接触模型开发了简易凸轮机构模型以及样条曲线接触应用示例。
1) 简易凸轮机构案例
2) 样条曲线插值接触案例
以上聊到的内容只是刚体接触动力学领域的一部分,目前在接触模型开发工作上仍有许多内容需要持续探索优化。比如在面对复杂几何接触问题时接触搜索算法对模型求解效率的优化、不同接触力计算方法对模型求解效率及求解精度的影响分析以及几何单元间因接触过渡产生的接触力误差的消除等。