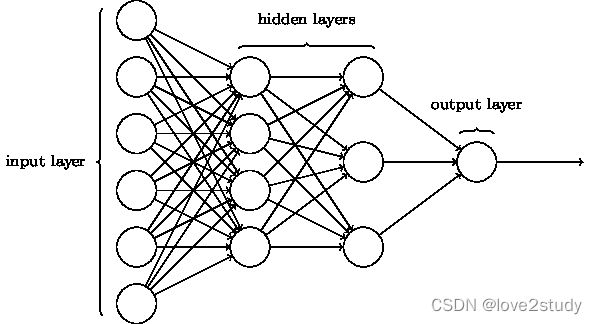
全连接神经网络 MLP
全连接神经网络–MLP
全连接神经网络,又叫多层感知机,是一种连接方式较为简单的人工神经网络,是前馈神经网络的一种。
MLP的神经网络架构
网络架构为:
通过输入层,隐藏层,输出层三个网络层组成,其中隐藏层可以有多层。
BP传播的原理
梯度下降法
正向传播,对网络层的输出进行传播,反向传播,对输入的梯度进行传播。
输出层:
- 偏置的梯度
- 权重的梯度
- 输入的梯度
中间层:
- 偏置的梯度
- 权重的梯度
- 输入的梯度
| 网络层 | 下表 | 神经元数量 |
|---|---|---|
| 输入层 | i | l |
| 中间层 | j | m |
| 输出层 | k | n |
输出层的梯度
相关函数
E = f 1 ( y k ) E=f_1(y_k) E=f1(yk)
y k = f 2 ( u k ) y_k=f_2(u_k) yk=f2(uk)
u k = ∑ q = 1 m ( y q w q k + b k ) u_k=\sum_{q=1}^{m}(y_qw_{qk}+b_k) uk=∑q=1m(yqwqk+bk)
E:损失值
f 1 f_1 f1:损失函数
y k y_k yk:输出结果
f 2 f_2 f2:激励函数
u k u_k uk:输入与权值乘积与偏置的求和
y j y_j yj: y j y_j yj为 y q y_q yq中的一个
定义
δ k = ∂ E ∂ u K = ∂ E ∂ y k ∂ y k ∂ u k \delta_k=\frac{∂E}{∂u_K}=\frac{\partial E}{\partial y_k}\frac{\partial y_k}{\partial u_k} δk=∂uK∂E=∂yk∂E∂uk∂yk
∂ E ∂ y k \frac{\partial E}{\partial y_k} ∂yk∂E损失函数对 y k y_k yk的偏微分
∂ y k ∂ u k \frac{\partial y_k}{\partial u_k} ∂uk∂yk激励函数对 u k u_k uk的偏微分
输出层权重的梯度
∂ w j k = ∂ E ∂ w j k \partial w_{jk} = \frac{\partial E}{\partial w_{jk}} ∂wjk=∂wjk∂E
根据微分连锁公式
∂ E ∂ w j k = ∂ E ∂ y k ∂ y k ∂ u k ∂ u k ∂ w j k \frac{\partial E}{\partial w_{jk}}=\frac{\partial E}{\partial y_k}\frac{\partial y_k}{\partial u_k}\frac{\partial u_k}{\partial w_{jk}} ∂wjk∂E=∂yk∂E∂uk∂yk∂wjk∂uk
∂ u k ∂ w j k = y j \frac{\partial u_k}{\partial w_{jk}}=y_j ∂wjk∂uk=yj : u k u_k uk对 w j k w_{jk} wjk的偏微分
∂ w j k = δ k y j \partial w_{jk} =\delta_ky_j ∂wjk=δkyj
输出层偏置的梯度
∂ b k = ∂ E ∂ b k \partial b_k = \frac{\partial E}{\partial b_k} ∂bk=∂bk∂E
根据微分连锁公式
∂ E ∂ b k = ∂ E ∂ y k ∂ y k ∂ u k ∂ u k ∂ b k \frac{\partial E}{\partial b_k}=\frac{\partial E}{\partial y_k}\frac{\partial y_k}{\partial u_k}\frac{\partial u_k}{\partial b_k} ∂bk∂E=∂yk∂E∂uk∂yk∂bk∂uk
∂ u k ∂ b k = 1 \frac{\partial u_k}{\partial b_k}=1 ∂bk∂uk=1 u k u_k uk对 b k b_k bk的偏微分
∂ b k = δ k \partial b_k =\delta_k ∂bk=δk
输出层的输入梯度
输出层的输入梯度=中间层的输出梯度
∂ y j = ∂ E ∂ y j \partial y_j= \frac{\partial E}{\partial y_j} ∂yj=∂yj∂E
根据微分连锁公式
∂ E ∂ y j = ∑ r = 1 n ∂ E ∂ y r ∂ y r ∂ u r ∂ u r ∂ y j \frac{\partial E}{\partial y_j}=\sum_{r=1}^{n}\frac{\partial E}{\partial y_r}\frac{\partial y_r}{\partial u_r}\frac{\partial u_r}{\partial y_j} ∂yj∂E=∑r=1n∂yr∂E∂ur∂yr∂yj∂ur
∂ u r ∂ y j = w j r \frac{\partial u_r}{\partial y_j}=w_{jr} ∂yj∂ur=wjr
∂ y j = ∑ r = 1 n δ r w j r \partial y_j=\sum_{r=1}^{n}\delta_rw_{jr} ∂yj=∑r=1nδrwjr
中间层的梯度
相关函数
y j = f ( u j ) y_j=f(u_j) yj=f(uj)
u j = w i j y i + b j u_j=w_{ij}y_i+b_j uj=wijyi+bj
y j y_j yj为中间层的输出值
f f f为激励函数
u j u_j uj输入值与权重的乘积与偏置的和
中间层权重的梯度
∂ w i j = ∂ E ∂ w i j = ∂ E ∂ u j ∂ u j ∂ w i j = ∂ E ∂ y j ∂ y j ∂ u j ∂ u j ∂ w i j ∂ w_{ij}=\frac{∂ E}{∂ w_{ij}}=\frac{∂ E}{∂ uj}\frac{∂{u_j}}{∂ w_{ij}}=\frac{∂ E}{∂ y_j}\frac{∂ y_j}{∂ u_j}\frac{∂ u_j}{∂ w_{ij}} ∂wij=∂wij∂E=∂uj∂E∂wij∂uj=∂yj∂E∂uj∂yj∂wij∂uj
∂ E ∂ y j \frac{∂ E}{∂ y_j} ∂yj∂E为中间层的输出梯度
∂ y j ∂ u j \frac{∂ y_j}{∂ u_j} ∂uj∂yj为激励函数的微分
∂ u j ∂ w i j = y i \frac{∂ u_j}{∂ w_{ij}}=y_i ∂wij∂uj=yi
定义 δ j = ∂ y i ∂ y j ∂ u j \delta_j=∂ y_i\frac{∂ y_j}{∂ u_j} δj=∂yi∂uj∂yj则 ∂ w i j = y i δ j ∂ w_{ij}=yi\delta_j ∂wij=yiδj
中间层偏置的梯度
∂ b j = ∂ E ∂ b j = ∂ E ∂ u j ∂ u j ∂ b j ∂ b_j=\frac{∂ E}{∂ b_j}=\frac{∂ E}{∂ uj}\frac{∂{u_j}}{∂ b_j} ∂bj=∂bj∂E=∂uj∂E∂bj∂uj
∂ u j ∂ b j = 1 \frac{∂{u_j}}{∂ b_j}=1 ∂bj∂uj=1
则 b j = δ j b_j=\delta_j bj=δj
若网络层不止三层,即隐藏层不止三层,则 ∂ y i = ∑ q = 1 m ∂ q w i q ∂ y_i=\sum_{q=1}^{m}∂_qw_{iq} ∂yi=∑q=1m∂qwiq
梯度计算公式总结
输出层
δ k = ∂ E ∂ u k = ∂ E ∂ y k ∂ y k ∂ u k \delta_k=\frac{\partial E}{\partial u_k}=\frac{\partial E}{\partial y_k}\frac{\partial y_k}{\partial u_k} δk=∂uk∂E=∂yk∂E∂uk∂yk
∂ w j k = y j δ k \partial w_{jk} =y_j\delta_k ∂wjk=yjδk
∂ b k = δ k \partial b_k =\delta_k ∂bk=δk
∂ y j = ∑ r = 1 n δ r w j r \partial y_j=\sum_{r=1}^{n}\delta_rw_{jr} ∂yj=∑r=1nδrwjr
关于 δ k \delta_k δk的求解,在使用不同的损失函数和激励函数组合时不同,其方法也是不同的, δ k \delta_k δk与输出层的神经元数量相同
中间层
δ j = ∂ E ∂ u j = ∂ y i ∂ y j ∂ u j \delta_j=\frac{∂ E}{∂ u_j}=∂ y_i\frac{∂ y_j}{∂ u_j} δj=∂uj∂E=∂yi∂uj∂yj
∂ w i j = y i δ j ∂ w_{ij}=y_i\delta_j ∂wij=yiδj
∂ b j = δ j ∂ b_j=\delta_j ∂bj=δj
∂ y i = ∑ q = 1 m δ q w i q ∂ y_i=\sum_{q=1}^{m}\delta_qw_{iq} ∂yi=∑q=1mδqwiq
MLP的建构
import torch
import torch.nn as nn
def self_MLP(nn.module):
def __init__(self):
super(self_MLP,self).__init__()
self.hidden = nn.Sequential(
nn.Linear(10,128); # 10个输入,第一层隐藏层为10个神经元
nn.ReLU(); # 激活函数为ReLU()函数
nn.Linear(128,64); # 第二个隐藏层为64个神经元
nn.ReLU();
nn.Linear(64,32); # 第三个隐藏层为32个神经元
nn.ReLU();
)
def forward(self,x):
x = self.hidden(x)
return x # 返回x