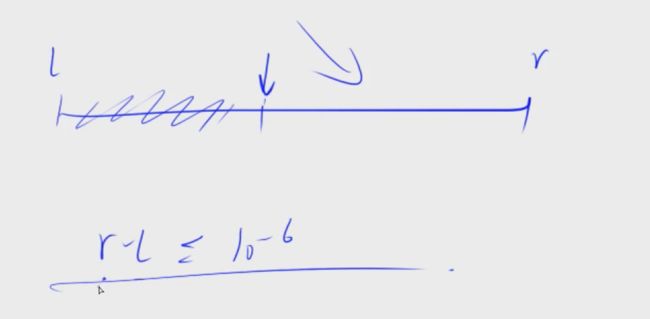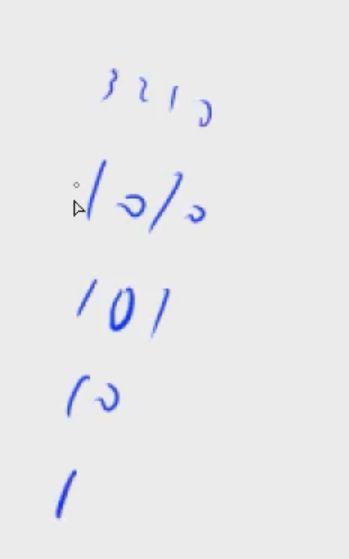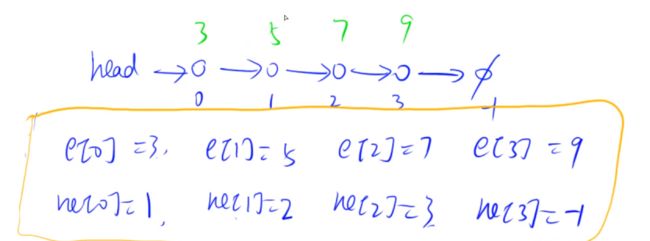算法基础课 acwing

算法基础课

本博客基于acwing算法基础课,所做笔记
目的在于方便复习
课程链接:https://www.acwing.com/activity/content/introduction/11/
主讲人:yxc

上课的时候理解算法的主要思想

课后把模板背过,并且调试题目,多重复,多敲

第一讲 基础算法

快速排序

调整区间的方法:

1、暴力，需要开辟两个数组

2、双指针

1、i往后面扫描，当i指向的数字小于等于x，就继续往后，当指向的数字大于x的时候停下

2、此时j往前面扫描，当j指向的数字大于x，就继续往前，当指向的数字小于x的时候，停下

3、此时i指向的大于x，j指向的小于x，那么这两个数字交换，并且两个指针都往中间移动一位，直到i和j穿过

可以发现，任何时候，i右边的数字都小于等于x，j左边的数字都大于x

模板：

void quick_sort(int q[],int l,int r){
	if(l >= r) return;				// 如果区间内只有一个或者没有数字，跳出循环
	
	int x = q[l + r >> 1],i = l -1,j = r + 1;
	
	while(i < j){
		do i++; while(q[i] < x);
		do j--; while(q[j] > x);
		if(i < j) swap(q[i],q[j]);
	}
	
	quick_sort(q,l,j);
	quick_sort(q,j+1,r);
}

快速排序

https://www.acwing.com/problem/content/787/

#include 

using namespace std;

const int N = 1e6 + 10;

int q[N];

void quick_sort(int q[],int l,int r){
	if(l >= r) return;	
	
	int x = q[l + r >> 1],i = l -1,j = r + 1;
	
	while(i < j){
		do i++; while(q[i] < x);
		do j--; while(q[j] > x);
		if(i < j) swap(q[i],q[j]);
	}
	
	quick_sort(q,l,j);
	quick_sort(q,j+1,r);
}

int main(){
	int n;
	scanf("%d",&n);
	for(int i = 0;i < n;i++) scanf("%d",&q[i]);
	
	quick_sort(q,0,n-1);
	
	for(int i = 0;i < n;i++) printf("%d ",q[i]);
	
	return 0;
}

第k个数

https://www.acwing.com/problem/content/788/

#include 

using namespace std;

const int N = 1e5 + 10;

int a[N],n,k;

int quick_sort(int l,int r,int k){
	if(l == r) return a[l];
	
	int i = l - 1,j = r + 1,x = a[(l+r) >> 1];
	while(i < j){
		while(a[++ i] < x);		// 这里只能是++i,不能是i-- 
		while(a[-- j] > x);
		if(i < j)  swap(a[i],a[j]);
	}
	int sl = j - l + 1;
	if(k <= sl) return quick_sort(l,j,k);
	else return quick_sort(j+1,r,k-sl);
}

int main(){
	scanf("%d%d",&n,&k);
	for(int i = 0 ;i < n;i++) scanf("%d",&a[i]);
	printf("%d\n",quick_sort(0,n-1,k));
	return 0;
}

快速选择算法

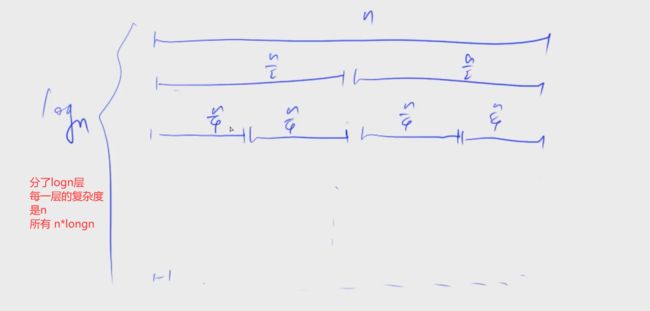
归并排序

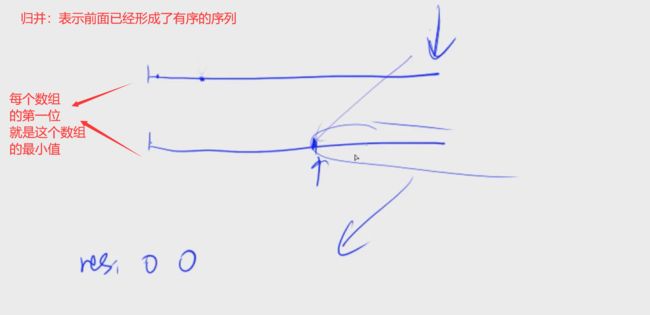
如何归并

双指针

归并的思路：

1、先递归，将序列一直分半，直到只剩一个元素

2、归并，归并采取双指针

模板：

void merge_sort(int q[],int l,int r){
	if(l >= r) return;				// 如果区间只有一个或者没有数字，不用递归了 
	
	int mid = (l + r) >> 1;			// mid是中间那个数字 
	
	merge_sort(q,l,mid);			// 归并排序先递归 
	merge_sort(q,mid+1,r);			// 分到最后就只剩一个数字了 
	
	int k = 0,i = l,j = mid + 1;	// 归并，使用双指针，i指向左半边的起点，j指向右半边的起点 
	while(i <= mid && j <= r){		
		if(q[i] <= q[j]) tmp[k++] = q[i++];
		else tmp[k++] = q[j++];
	}
	while(i <= mid) tmp[k++] = q[i++];
	while(j <= r) tmp[k++] = q[j++];
	
	for(i = l,j = 0;i <= r;i++,j++) q[i] = tmp[j];
}

归并排序

https://www.acwing.com/problem/content/789/

#include 

using namespace std;

const int N = 1e6 + 10;

int q[N],tmp[N],n;

void merge_sort(int q[],int l,int r){
	if(l >= r) return;				// 如果区间只有一个或者没有数字，不用递归了 
	
	int mid = (l + r) >> 1;			// mid是中间那个数字 
	
	merge_sort(q,l,mid);			// 归并排序先递归 
	merge_sort(q,mid+1,r);			// 分到最后就只剩一个数字了 
	
	int k = 0,i = l,j = mid + 1;	// 归并，使用双指针，i指向左半边的起点，j指向右半边的起点 
	while(i <= mid && j <= r){		
		if(q[i] <= q[j]) tmp[k++] = q[i++];
		else tmp[k++] = q[j++];
	}
	while(i <= mid) tmp[k++] = q[i++];
	while(j <= r) tmp[k++] = q[j++];
	
	for(i = l,j = 0;i <= r;i++,j++) q[i] = tmp[j];
}

int main(){
	scanf("%d",&n);
	for(int i = 0;i < n;i++) scanf("%d",&q[i]);
	
	merge_sort(q,0,n-1);
	
	for(int i = 0;i < n;i++) printf("%d ",q[i]);
	
	return 0;
}

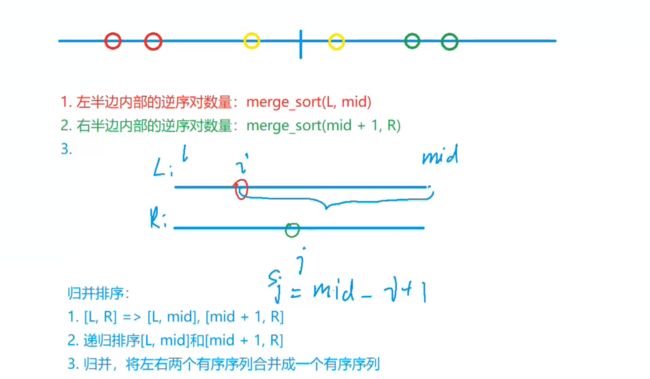
逆序对的数量

https://www.acwing.com/problem/content/790/

#include  

using namespace std;

const int N = 1e5 + 10;

int a[N],temp[N];

long long merge_sort(int l,int r){
	if(l >= r) return 0;
	
	int mid = (l + r) >> 1;
	long long res = merge_sort(l,mid) + merge_sort(mid+1,r);
	
	// 归并
	int k = 0,i = l,j = mid + 1;
	while(i <= mid && j <= r) {
		if(a[i] <= a[j]) temp[k++] = a[i++];
		else {
			temp[k++] = a[j++];
			res += mid - i + 1;
		}
	}
	
	while(i <= mid) temp[k++] = a[i++];
	while(j <= r) temp[k++] = a[j++];
	
	for(i = l,k = 0;i <= r;i++,k++) a[i] = temp[k];
	return res;
}

int main(){
	int n;
	scanf("%d",&n);
	for(int i = 0;i < n;i++) scanf("%d",&a[i]);
	printf("%lld\n",merge_sort(0,n-1));
	return 0;
}

二分

模板：https://www.acwing.com/blog/content/31/

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

数的范围

https://www.acwing.com/problem/content/791/

#include 

using namespace std;

const int N = 1e5 + 10;

int q[N],m,n;

int main(){
	scanf("%d %d",&n,&m);
	for(int i = 0;i < n;i++) scanf("%d",&q[i]);
	
	while(m--){
		int x;
		scanf("%d",&x);
		// 先不管check函数，先把l，r和while，mid写好 
		int l = 0,r = n - 1;
		while(l < r){
			int mid = (l + r) >> 1;
			if(q[mid] >= x) r = mid;
			else l = mid + 1;
		}
		if(q[l] != x) puts("-1 -1");
		else{
			printf("%d ",l);
			l = 0,r = n - 1;
			while(l < r){
				int mid = (l + r + 1) >> 1;
				if(q[mid] <= x) l = mid;
				else r = mid - 1;
			}
			printf("%d\n",l);
		}
	}
	return 0;
}

浮点数二分

开平方

#include 

using namespace std;

int main(){
	double x;
	cin >> x;
	
	double l = 0,r = x;
	while(r - l > 1e-6){
		double mid = (l + r) / 2;
		if(mid * mid >= x) r = mid;
		else l = mid;
	}
	printf("%lf\n",l);
	return 0;
}

数的三次方根

https://www.acwing.com/problem/content/792/

#include 

using namespace std;

int main(){
	double n;
	scanf("%lf",&n);
	double l = -10000,r = 10000;
	while(r-l > 1e-8){
		double mid = (l + r) / 2;
		if(mid * mid * mid > n) r = mid;
		else l = mid;
	}
	printf("%lf\n",l);
	return 0;
}

高精度

前缀和

一维前缀和

前缀和

https://www.acwing.com/problem/content/797/

预处理:O(n)

#include  

using namespace std;

const int N = 1e5 + 10;

int a[N],s[N];

int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i++) {
		scanf("%d",&a[i]);
		s[i] = s[i-1] + a[i];	// 前缀和数组的初始化
	}
	while(m--){
		int l,r;
		scanf("%d%d",&l,&r);
		printf("%d\n",s[r]-s[l-1]);
	}
	return 0;
}

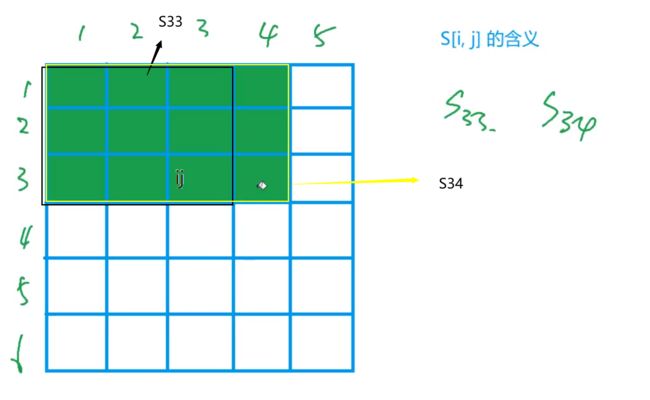
二维前缀和

S[i,j]的含义:这个格子左上角面积之和

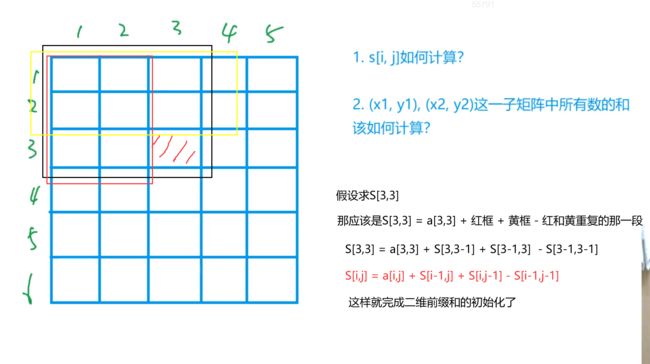
S[i,j]计算方法:

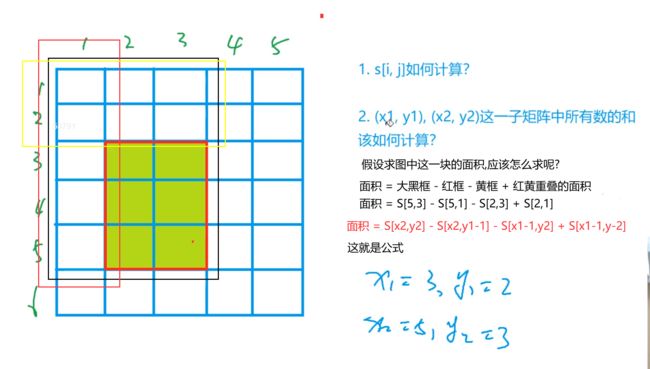
(x1,y1),(x2,y2)子矩阵中所有数之和怎么计算?

子矩阵的和

https://www.acwing.com/problem/content/798/

#include 

using namespace std;

const int N = 1e3 + 10;

int a[N][N],s[N][N];

int main(){
	int n,m,q;
	scanf("%d%d%d",&n,&m,&q);
	for(int i = 1;i <= n;i++){
		for(int j = 1;j <= m;j++){
			scanf("%d",&a[i][j]);
			// 初始化二维前缀和 	
			s[i][j] = a[i][j] + s[i-1][j] + s[i][j-1] - s[i-1][j-1];	
		}
	}
	while(q--){
		int x1,y1,x2,y2;
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		// 计算差 
		printf("%d\n",s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]);
	}
	return 0;
}

差分

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-z6zhrdDJ-1630933432550)(https://gitee.com/Crescent_P/picture-bed/raw/master/hh.png)]差分数组不需要构造

一维差分

https://www.acwing.com/problem/content/799/

#include  

using namespace std;

const int N = 1e5 + 10;

int a[N],b[N];

// 插入函数,使得b[l] + c,b[r+1] - c 
void insert(int l,int r,int c){
	b[l] += c;
	b[r + 1] -= c;
}

int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i++){
		scanf("%d",&a[i]);
		// 差分数组不需要构建,先假设a数组为全零,那么b数组也就为全零
        // [1,1]插入a[1],[2,2]插入a[2]
		// 就能构造出差分数组 
		insert(i,i,a[i]);
	}
	while(m--){
		int l,r,c;
		scanf("%d%d%d",&l,&r,&c);
		insert(l,r,c);
	}
	for(int i = 1;i <= n;i++) {
		a[i] = a[i-1] + b[i];
		printf("%d ",a[i]);
	}
}

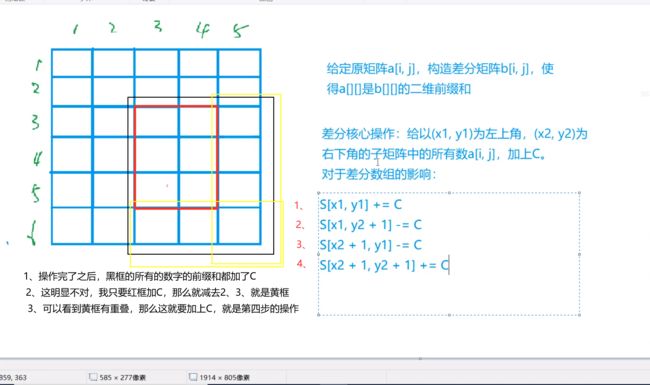
二维差分

差分矩阵

https://www.acwing.com/problem/content/800/

#include  

using namespace std;

const int N = 1e3 + 10;

int a[N][N],b[N][N];

// 插入公式
void insert(int x1,int y1,int x2,int y2,int c){
	b[x1][y1] += c;
	b[x1][y2+1] -= c;
	b[x2+1][y1] -= c;
	b[x2+1][y2+1] += c;
}

int main(){
	int n,m,q;
	scanf("%d%d%d",&n,&m,&q);
	for(int i = 1;i <= n;i++){
		for(int j = 1;j <= m;j++){
			scanf("%d",&a[i][j]);
            // 构建差分数组b
			insert(i,j,i,j,a[i][j]);
		}
	}
	while(q--){
		int x1,y1,x2,y2,c;
		scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
		insert(x1,y1,x2,y2,c);
	}
	for(int i = 1;i <= n;i++){
		for(int j = 1;j <= m;j++){
			a[i][j] = b[i][j] + a[i-1][j] + a[i][j-1]  - a[i-1][j-1];
			printf("%d ",a[i][j]);
		}
		printf("\n");
	}
	return 0;
}

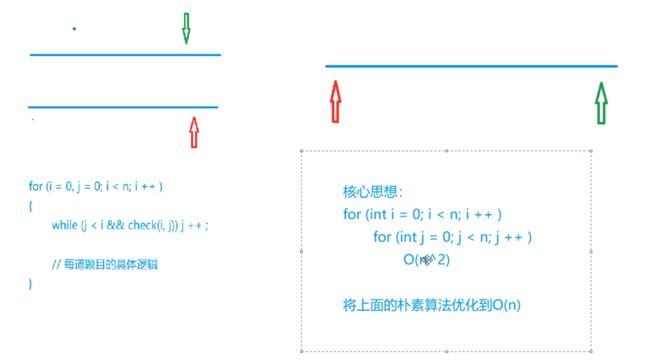
双指针算法

输出单词

#include  

using namespace std;

int main(){
	char str[1000];
	
	gets(str);
	
	int n = strlen(str);
	
	for(int i = 0;i < n;i++){
		int j = i;
		while(j < n && str[j] != ' ') j++;
		
		// 这道题的具体逻辑 
		for(int k = i;k < j;k++) printf("%c",str[k]);
		puts("");
		i = j;
	}
	return 0;
}

最长连续不重复子序列

https://www.acwing.com/problem/content/801/

暴力:O(n^2)

#include 

using namespace std;

const int N = 1e5 + 10;

int a[N],b[N];

int main(){
	int n;
	scanf("%d",&n);
	for(int i = 0;i < n;i++) scanf("%d",&a[i]);
	int ans = 0;
	for(int i = 0;i < n;i++){
		b[a[i]]++;
		for(int j = i+1;j < n;j++){
			if(b[a[j]] != 0) break;
			b[a[j]]++;
			ans = max(ans,j - i + 1);
		}
		b[a[i]]--;
		for(int i = 0;i < n;i++) b[i] = 0;
	}
	printf("%d\n",ans);
	return 0;
}

双指针:O(n)

#include  

using namespace std;

const int N = 1e5 + 10;

int a[N],b[N];

int main(){
	int n;
	scanf("%d",&n);
	for(int i = 0;i < n;i++) scanf("%d",&a[i]);
	int ans = 0;
	for(int i = 0,j = 0;i < n;i++){
		while(j < n && b[a[j]] == 0){
			ans = max(ans,j - i + 1);
			b[a[j++]]++;
		}
		b[a[i]]--;
	}
	printf("%d\n",ans);
	return 0;
}

数组元素的目标和

https://www.acwing.com/problem/content/802/

#include 

using namespace std;

const int N = 1e5 + 10;

int a[N],b[N],n,m,x;

int main(){
	scanf("%d%d%d",&n,&m,&x);
	for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
	for(int j = 1;j <= m;j++) scanf("%d",&b[j]);
	for(int i = 1,j = m;i <= n ;i++){
		while(j <= m && a[i] + b[j] > x) j--;
		if(a[i] + b[j] == x) {
			printf("%d %d",i-1,j-1);
			break;
		}
	}
	return 0;
}

判断子序列

https://www.acwing.com/problem/content/description/2818/

#include 

using namespace std;

const int N = 1e5 + 10;

int n,m;
int a[N],b[N];

int main(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
	for(int j = 1;j <= m;j++) scanf("%d",&b[j]);
	
	bool flag = true;
	for(int i = 1,j = 1;i <= m && flag;i++){
		while(j <= n && b[i] == a[j]) j++,i++;
		// 移动到最后一位后面了 
		if(j == n+1) flag = false;
	}
	if(flag) puts("No");
	else puts("Yes");
	
	return 0;
}

位运算

可以求出10的二进制表示

#include  

using namespace std;

int main(){
	int n = 10;
	
	for(int k = 3;k >= 0;k-- ) printf("%d",(n>>k)&1);
	
	return 0;
}

lowbit运算

二进制中1的个数

https://www.acwing.com/problem/content/803/

#include  

using namespace std;

int lowbit(int x){
	return x & -x;
}

int main(){
	int n;
	scanf("%d",&n);
	while(n--){
		int x;
		scanf("%d",&x);
		
		int res = 0;
		// 每次减去x的最后一位1 
		while(x) x -= lowbit(x), res++;
		printf("%d ",res);
	}
	return 0;
}

离散化

区间和

https://www.acwing.com/problem/content/804/

#include 

using namespace std;

typedef pair PII;

const int N = 3e5 + 10;


int n,m;
int a[N],s[N];

vector alls;
vector add,query;

// 通过x的值找到下标,将一个值序列,映射到从1开始的数组 
int find(int x){
	int l = 0,r = alls.size() - 1;
	while(l < r){
		int mid = (l + r) >> 1;
		if(alls[mid] >= x) r = mid;
		else l = mid + 1;
	}
	return r + 1;
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i = 0;i < n;i++){
		int x,c;
		scanf("%d%d",&x,&c);
		add.push_back({x,c});
		
		alls.push_back(x);
	}
	
	for(int i = 0;i < m;i++){
		int l,r;
		scanf("%d%d",&l,&r);
		query.push_back({l,r});
		
		alls.push_back(l);
		alls.push_back(r);
	}
	
	// 去重 
	sort(alls.begin(),alls.end());
	alls.erase(unique(alls.begin(),alls.end()),alls.end());
	// 上面操作完,是一个去重并且排序后的一个数组 
	// 处理插入 
	for(auto item: add)	{
		int x = find(item.first);
		// 上面x是通过值找到的下标,x是下标 
		a[x] += item.second;
	}
	
	// 预处理前缀和
	for(int i= 1;i <= alls.size();i++) s[i] = s[i-1] + a[i];
	
	// 处理询问 
	for(auto item : query) {
		int l = find(item.first);
		int r = find(item.second);
		printf("%d\n",s[r] - s[l-1]);
	}
	return 0;
}

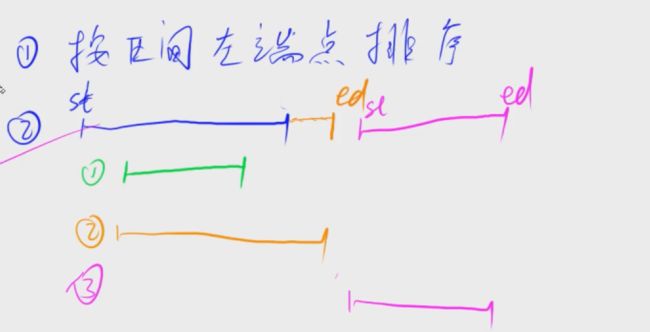
区间合并

区间合并

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2x7KVK5l-1630933432558)(算法基础课.assets/image-20210830163830687.png)]

https://www.acwing.com/problem/content/805/

#include 

using namespace std;

typedef pair PII;

const int N = 1e5 + 10;

int n;
vector segs;

void merge(vector &segs){
	vector res;
	
	// 以左端点排序 
	sort(segs.begin(),segs.end());
	
	int st = -2e9,ed = -2e9;
	
	for(auto seg : segs){
		// 没有交集 
		if(ed < seg.first){
			if(st != -2e9) res.push_back({st,ed});
			st = seg.first,ed = seg.second;
		}else ed = max(ed,seg.second);
	}
	
	// 最后一个 
	if(st != -2e9) res.push_back({st,ed});
	segs = res;
}

int main(){
	scanf("%d",&n);
	
	for(int i = 0;i < n;i++){
		int l,r;
		scanf("%d%d",&l,&r);
		segs.push_back({l,r});
	}
	
	merge(segs);
	
	printf("%d\n",segs.size());
	
	return 0;
}

第二讲 数据结构

单链表

用数组模拟链表

e数组存值,ne数组存next

单链表

https://www.acwing.com/problem/content/828/

#include 

using namespace std;

const int N = 1e5 + 10;

// head 表示头结点的下标
// e[i] 表示节点i的值
// ne[i] 表示节点i的next指针是多少
// 存储到当前用到了哪个点 
int head,inx,e[N],ne[N];

// 初始化 
void init(){
	// 初始化,链表为空,-1表示空集 
	head = -1;
	inx = 0; 
}

// 将x插到头结点,就是让x成为头结点 
void add_to_head(int x) {
	e[inx] = x;
	ne[inx] = head;
	// head 表示头结点的下标,head不是一个节点哦 
	head = inx;
	inx++;
}

// 将x插入到下标是k的节点的后面 
void add(int k,int x){
	e[inx] = x;
	ne[inx] = ne[k];
	ne[k] = inx;
	inx++;
}

// 将下标是k的点的后面的点删除 
void remove(int k){
	ne[k] = ne[ne[k]];
}

int main(){
    int M;
    scanf("%d",&M);
    init();
    while(M--){
        int k,x;
        char op;
        cin >> op;
        if(op == 'H'){
            scanf("%d",&x);
            add_to_head(x);
        }else if(op == 'D'){
            scanf("%d",&k);
            // 删除头结点,就是让head指向头结点的下一个
            if (!k) head = ne[head];
            else remove(k-1);
        }else{
            scanf("%d%d",&k,&x);
            add(k-1,x);
        }
    }
    for(int i = head;i != -1;i = ne[i]) printf("%d ",e[i]);
    return 0;
}

双链表

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jF276k9j-1630933432561)(算法基础课.assets/image-20210831153743826.png)]

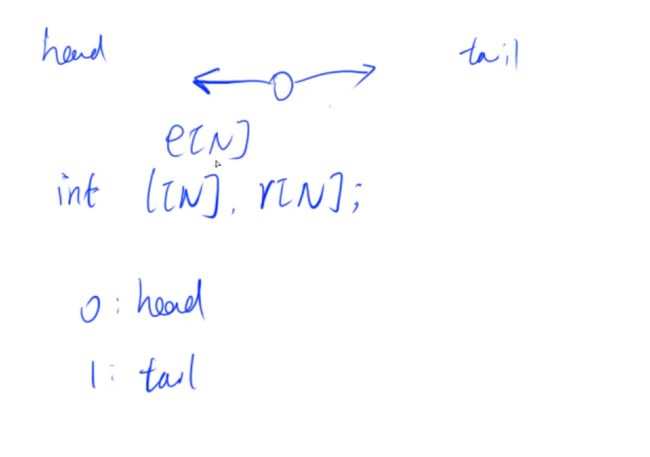
双链表

https://www.acwing.com/problem/content/829/

#include 

using namespace std;

const int N = 1e5 + 10;

int e[N],l[N],r[N],idx;

// 初始化 
void init(){
	// 0 表示右端点
	// 1 表示左端点
	r[0] = 1,l[1] = 0;
	idx = 2;
}

// 在下标是k的点的右边,插入x 
void add(int k,int x){
	e[idx] = x;
	l[idx] = k;
	r[idx] = r[k];
	r[k] = idx;
	l[r[idx]] = idx;
	idx++;
}

// 删除第k个点 
void remove(int k) {
	r[l[k]] = r[k];
	l[r[k]] = l[k];
}


int main(){
	int M;
	scanf("%d",&M);
	init();
	while(M--){
		int x,k;
		string op;
		cin >> op;
		if(op == "L"){
			scanf("%d",&x);
			add(0,x);
		}else if(op == "R"){
			scanf("%d",&x);
			add(l[1],x);
		}else if(op == "D"){
			scanf("%d",&k);
			// idx从2开始,第k个点的下标应该是k+1
			remove(k+1);
		}else if(op == "IL"){
			scanf("%d%d",&k,&x);
			add(l[k+1],x);
		}else{
			scanf("%d%d",&k,&x);
			add(k+1,x);
		}
	}
	
	for(int i = r[0];i != 1;i = r[i]) printf("%d ",e[i]);
	return 0;
}

栈

先进后出

模拟栈

https://www.acwing.com/problem/content/830/

#include  

using namespace std;

const int N = 1e5 + 10;

// tt 是栈顶坐标 
int stk[N],tt;

void push(int x) {
	stk[++tt] = x;
}

void pop(){
	tt--;
}

bool empty(){
	if(tt == 0) return true;
	else return false;
}

int query(){
	return stk[tt];
}

int main(){
	int M;
	scanf("%d",&M);
	while(M--){
		string op;
		int x;
		cin >>op;
		if(op == "push"){
			scanf("%d",&x);
			push(x);
		}else if(op == "pop"){
			pop();
		}else if(op == "query"){
			printf("%d\n",query());
		}else{
			if(empty()) printf("YES\n");
			else printf("NO\n");
		}
	}
	return 0;
}

队列

先进先出

模拟队列

https://www.acwing.com/problem/content/831/

#include 

using namespace std;

const int N = 1e5+10;

// 在队尾插入元素,在队头弹出原始 
int q[N],hh,tt = -1;

void push(int x) {
	q[++ tt] = x;
}

void pop(){
	hh++;
}

bool empty(){
	if(hh <= tt) return false;
	else return true;
}

int query(){
	return q[hh];
}

int main(){
	int M;
	scanf("%d",&M);
	while(M--){
		string op;
		int x;
		cin >> op;
		if(op == "push"){
			scanf("%d",&x);
			push(x);
		}else if(op == "pop"){
			pop();
		}else if(op == "query"){
			printf("%d\n",query());
		}else{
			if(empty()) printf("YES\n");
			else printf("NO\n");
		}
	}
	return 0;
}

单调栈

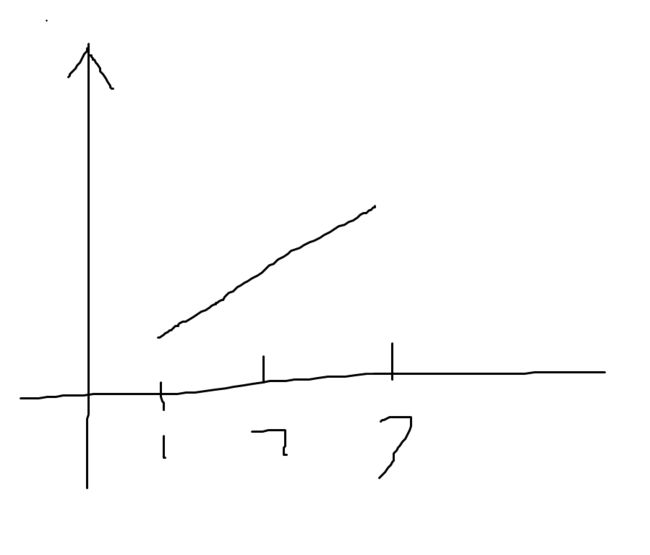
单调栈

常见模型：找出每个数左边离它最近的比它大/小的数

https://www.acwing.com/problem/content/description/832/

O(n)

#include 

using namespace std;

const int N = 1e5 + 10;

int n;
// tt一开始指向0,指向0表示没有元素 
int stk[N],tt;

int main(){
	scanf("%d",&n);
	for(int i = 0;i < n;i++){
		int x;
		scanf("%d",&x);
		// 如果栈不空,并且栈顶元素大于x,弹栈 
		while(tt && stk[tt] >= x) tt--;
		// 如果栈不空,输出栈顶 
		if(tt) printf("%d ",stk[tt]);
		else printf("-1 ");
		// 压栈,因为对于后面的元素而言,这个是离它最近,并且小的数了 
		stk[++tt] = x;
	}
	return 0; 
}

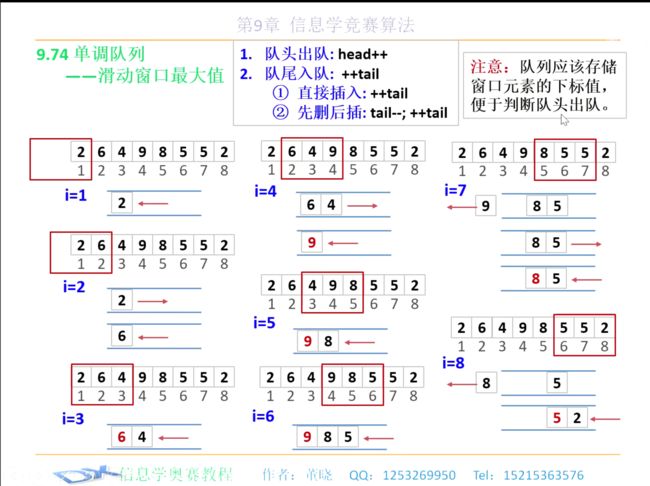
单调队列

常见模型：找出滑动窗口中的最大值/最小值

base on 董晓 : https://www.bilibili.com/video/BV1H5411j7o6

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-R3TivCQf-1630933432561)(https://gitee.com/Crescent_P/picture-bed/raw/master/image-20210901142939496.png)]

滑动窗口

https://www.acwing.com/problem/content/156/

#include  

using namespace std;

const int N = 1e6 + 10;

int a[N],q[N],hh,tt = -1;

int main(){
	int n,k;
	scanf("%d%d",&n,&k);
	for(int i = 0;i < n;i++) scanf("%d",&a[i]);
	for(int i = 0;i < n;i++){
		// q[hh] 不在[i-k+1,i],队头出队,就是判断队头是否已经滑出了窗口
		// 队列中存的是下标 
		if(hh <= tt && q[hh] < i-k+1) hh++;
		// 如果要进来的元素比队列中的元素小,那么队尾元素出队,保证队列的元素是由小到大
		// 因为较小的还用的上,大了的就用不上了 
		while(hh <= tt && a[q[tt]] >= a[i]) tt--;
		// 当前元素的下标入队 
		q[++tt]  = i; 
		// 保证窗口内的元素足够才开始输出
		// 队首存的是最小元素的下标 
		if(i >= k - 1) printf("%d ",a[q[hh]]);
	}
	puts("") ;
	hh = 0,tt = -1;
	for(int i = 0;i < n;i++){
		if(hh <= tt && i-k+1>q[hh]) hh++;
		while(hh <= tt && a[q[tt]] <= a[i]) tt--;
		q[++tt] = i;
		if(i >= k-1 ) printf("%d ",a[q[hh]]);
	}
	return 0;
}

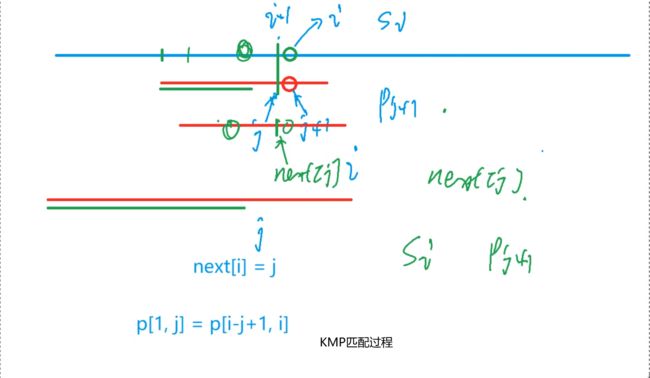
KMP

KMP字符串

https://www.acwing.com/problem/content/833/

#include 

using namespace std;

const int N = 1e4+10,M =  1e5+10;

int n,m;
char p[N],s[M];
int ne[N];

int main(){
	// 从第1位开始 
	cin >> n >> p+1 >> m >> s+1;
	
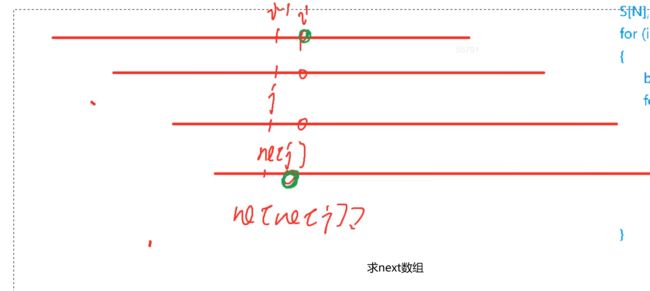
	// 求next数组 
	// next[1]=0,因为是j+1来匹配 
	for(int i = 2,j = 0;i <= n;i++) {
		// 如果匹配不成功 
		while(j && p[i]!=p[j+1]) j = ne[j];
		// 匹配成功 
		if(p[i] == p[j+1]) j++;
		ne[i] = j;
	}
	
	// kmp匹配过程
	for(int i = 1,j = 0;i <= m;i++) {
		while(j && s[i] != p[j+1]) j = ne[j];
		if(s[i] == p[j+1]) j++;
		// 匹配完了 
		if(j == n){
			// 下标从1开始的所以要减去1 ,应该是 i-n+1-1 
			printf("%d ",i-n);
			j = ne[j];	//
		}
	}
	return 0;
}

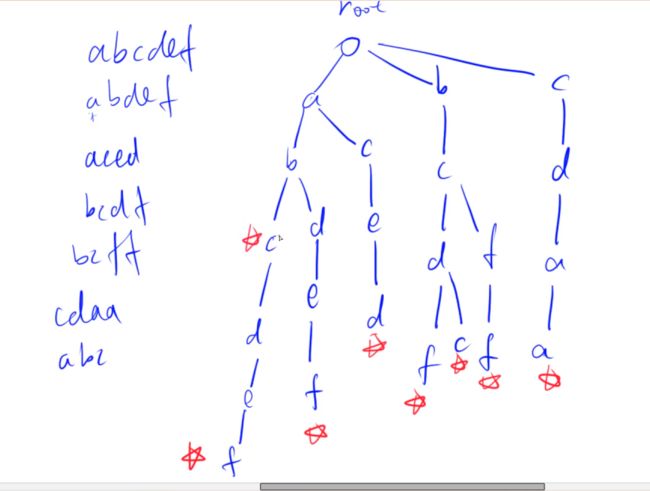
Trie

高效地存储和查找字符串集合的数据结构

要么全是大写,要么全是小写,要么全是数字,类型不会特别多

Trie字符串统计

https://www.acwing.com/problem/content/837/

#include  

using namespace std;

const int N = 1e5 + 10;

// 下标是0的点,既是根节点,又是空节点 
int son[N][26], cnt[N],idx;
char str[N];

void insert(char str[]){
	// 从根节点开始 
	int p = 0;
	// c++ 字符串以0结尾,就可以用这个来当条件 
	for(int i = 0;str[i];i++){
		// 将小写字母映射成数字 
		int u = str[i] - 'a';
		// 如果不存在这个子节点 
		if(!son[p][u]) son[p][u] = ++idx;
		p = son[p][u];
	}
	// 以这个点结尾的单词个数++ 
	cnt[p] ++;
}

int query(char str[]){
	int p = 0;
	for(int i = 0;str[i];i++){
		int u = str[i] - 'a';
		if(!son[p][u]) return 0;
		p = son[p][u];
	}
	return cnt[p];
}


int main(){
	int n;
	scanf("%d",&n);
	while(n--){
		char op[2];
		scanf("%s%s",&op,&str);
		if(op[0] == 'I') insert(str);
		else printf("%d\n",query(str));
	}
}

并查集

合并集合

https://www.acwing.com/problem/content/838/

#include 

using namespace std;

const int N = 1e5 + 10;

int n,m;
int p[N];

// 返回x祖宗节点 + 路径压缩 
int find(int x){
	// 如果不是根节点,就让他的父节点等于祖宗节点 
	if(p[x] != x) p[x] = find(p[x]);
	return p[x];
}

int main(){
	scanf("%d%d",&n,&m);
	
	for(int i = 1;i <= n;i++) p[i] = i;
	
	while(m--){
		char op[2];
		int a,b;
		scanf("%s%d%d",op,&a,&b);
		if(op[0] == 'M'){
			// a的祖宗节点的父节点 = b的祖宗节点 
			p[find(a)] = find(b);
		}else{
			if(find(a) == find(b)) puts("Yes");
			else puts("No");
		}
	}
	return 0;
} 

连通块中点的数量

https://www.acwing.com/problem/content/839/

#include 

using namespace std;

const int N = 1e5 + 10;

int n,m;
int p[N],size[N];

int find(int x){
	if(p[x] != x) p[x] = find(p[x]);
	return p[x];
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i++){
		p[i] = i;
		size[i] = 1;
	}
	while(m--){
		int a,b;
		char op[2];
		scanf("%s",op);
		if(op[0] == 'C'){
			scanf("%d%d",&a,&b);
			if(find(a) != find(b)) size[p[b]] += size[p[a]];
			p[find(a)] = find(b);
		}else if(op[1] == '1'){
			scanf("%d%d",&a,&b);
			if(find(a) == find(b)) puts("Yes");
			else puts("No");
		}else{
			scanf("%d",&a);
			printf("%d\n",size[find(a)]);
		}
	}
	return 0;
}

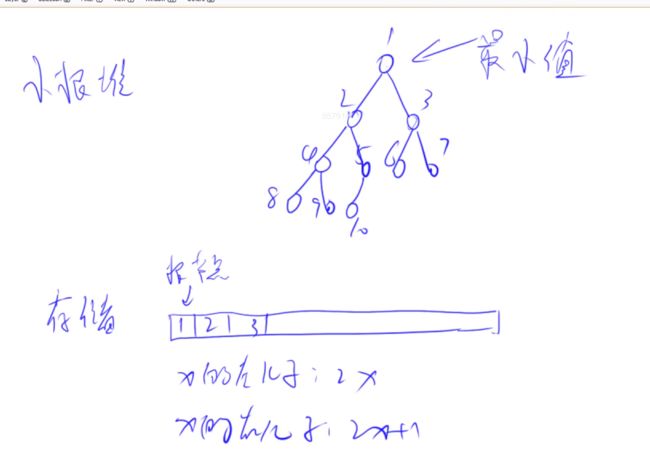
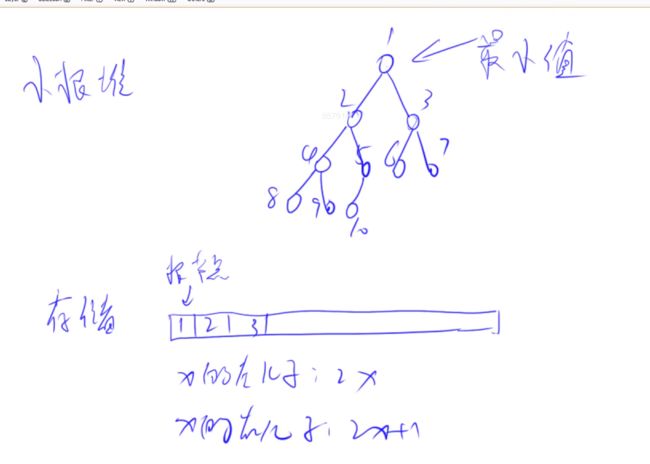
堆

哈希表

STL

/*
STL
vector						变长数组,倍增 
	size()	返回元素个数
	empty()	返回是否为空
	clear()	清空
	front()/back()
	push_back/pop_back()
	begin()/end()
	[]
	
pair 
	first 	第一个元素 
	second	第二个元素
	支持比较运算,按字典序,以first为第一关键字 
 
string						字符串(),substr,c_str() 
	size()/length()
	empty()
	clear()

queue		队列			
	push()		向队尾插入一个元素 
	front()		返回队头元素
	back()		返回队尾元素 
	pop() 		弹出队头元素
	 
priortity_queue 	优先队列,默认是大根堆 
	push()		插入一个元素 
	top()		返回堆顶元素 
	pop() 		弹出队头元素 

stack				栈	
	push() 		向栈顶插入元素 
	top()		返回栈顶元素 
	pop() 		弹出栈顶的元素 
	size()
	empty() 
deque			双端队列	 
	size()
	empty() 
	clear()
	front()
	back()
	push_back()/pop_back()
	push_front()/pop_front()
	begin()/end()
	[]
	 
set,map,multiset,multimap	基于平衡二叉树(红黑树),动态维护有序序列 
	size()
	empty()
	clear()
	begin()/end()	++,--	返回前驱和后继 
	
	set/multiset
		insert()	插入一个数 
		find()		查找一个数
		count()		返回一个数的个数
		erase()
			(1)	输入是一个数X,删除所有的X	O(k+logn) 
			(2) 输入是一个迭代器,删除这个迭代器 
		lower_bound/upper_bound()
			lower_bound(x)	 返回大于等于x的最小的数的迭代器 
			upper_bound(x) 	 返回大于x的最小的数的迭代器
			
	map/multimap
		insert()	插入的是一个pair 
		erase() 	输入的是pair或者迭代器
		find()
		[] 			O(logn)
		lower_bound/upper_bound()

// 无序的 
unordered_set,unordered_map,unordered_multiset,unordered_multimap 	哈希表 
	和上面类似,增删改查的时间复杂度是O(1) 
	不支持 lower_bound/upper_bound(),迭代器的++,-- 


bitset		压位 
	
	
*/ 

#include 

using namespace std;

int main() {
	// vector 
	// 定义vector 
	vector va;
	vector vb(10); 
	//长度为10,并且每个元素都是3 
	vector vc(10,3);
	for(int i = 0;i < 10;i++) va.push_back(i);
	// 三种遍历方式 
	for(int i = 0;i < 10;i++) printf("%d ",va[i]);
	puts("");
	for(vector::iterator i = va.begin();i != va.end();i++) printf("%d ",*i);
	puts("");
	for(auto x : va) printf("%d ",x);
	puts("");
	
	// pair
	pair  p;
	p = make_pair(1,"cp");
	p = {20,"cpcp"};
	
	// string
	string sa = "123";
	sa += "456";
	cout << sa << endl;
	
	// 子串,第一个参数起始地址,第二个参数长度 
	cout << sa.substr(2,4) << endl;
	// c_str(),字符串起始的长度 
	printf("%s\n",sa.c_str());
	
	// queue 队列 
	queue q;
	
//	q = queue;
	
	// 优先队列 
	priority_queue heap;							// 大根堆 
	
//	priority_queue> heap;	// 小根堆 
	
	// set
	
	// map
	map ma;
	ma["cp"]  = 1;
	printf("%d",ma["cp"]);
	
	return 0;
}

第三讲 搜索与图论

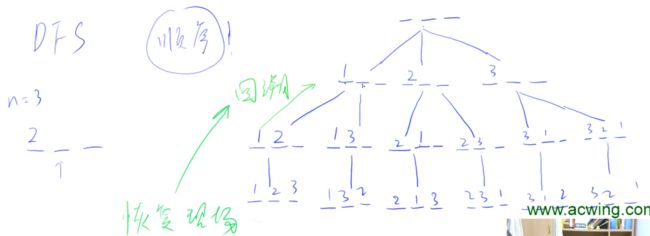
DFS

每个DFS都对应了一个搜索树

排列数字

https://www.acwing.com/problem/content/844/

#include  

using namespace std;

const int N = 10;

int n,path[N];
bool st[N];

void dfs(int u){
	if(u == n) {
	    for(int i = 0;i < n;i++) printf("%d ",path[i]);
	    puts("");
	    return;
	}
	for(int i = 1;i <=n;i++){
		if(!st[i]) {
			path[u] = i;
			st[i] = true;
			dfs(u+1);
			// 恢复现场 
			st[i] = false;
			path[u] = 0;
		}
	}
}

int main(){
	scanf("%d",&n);
	dfs(0);
	return 0;
}

BFS

走迷宫

https://www.acwing.com/problem/content/846/

#include 

using namespace std;

typedef pair PII;

const int N =110;

int n,m;
int g[N][N];
int d[N][N];
queue q;


int bfs(){
	q.push({0,0});
	memset(d,-1,sizeof d);
	d[0][0] = 0;
	int dx[4] = {1,0,-1,0},dy[4] = {0,1,0,-1};
	while(!q.empty()){
		auto t = q.front();
		q.pop();
		for(int i = 0;i < 4;i++){
			int x = t.first + dx[i];
			int y = t.second + dy[i];
			if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1){
				q.push({x,y});
				d[x][y] = d[t.first][t.second] + 1;
			}
		}
	}
	return d[n-1][m-1];
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i = 0;i < n;i++){
		for(int j = 0;j < m;j++) scanf("%d",&g[i][j]);
	}
	printf("%d\n",bfs());
	return 0;
}

树与图的深度优先遍历

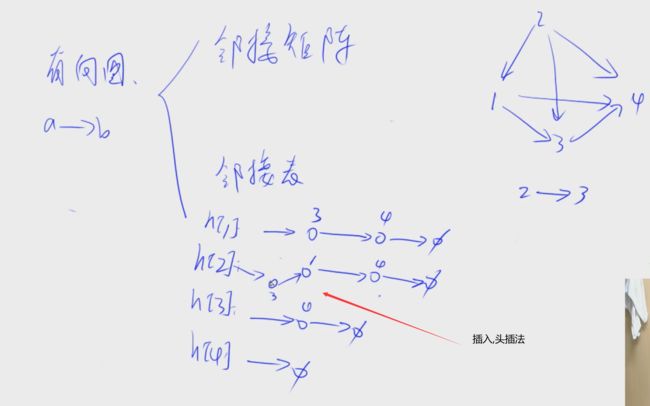
在算法题中,不管是有向图还是无向图,我们都视为有向图

如果是无向图,那么我们就设置一条a->b,再设置一条b->a的边就行了

图的深搜

#include 

using namespace std;

const int N = 1e5 + 10,M = N * 2;

int n,m;
int h[N],e[M],ne[M],idx;
bool st[N];

// 在a的链接表中,插入一个b 
void add(int a,int b){
	// 头插法 
	n[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}

// 深搜 
void dfs(int u){
	// 标记一下,已经被搜索过了 
	st[u] = true;
	// 遍历连接表 
	for(int i = h[u];i != -1;i = ne[i]){
		int j = e[i];
		if(!st[j]) dfs(j);
	}
}




int main(){
	// 都没有连接,-1表示尾节点 
	memset(h,-1,sizeof h);
}

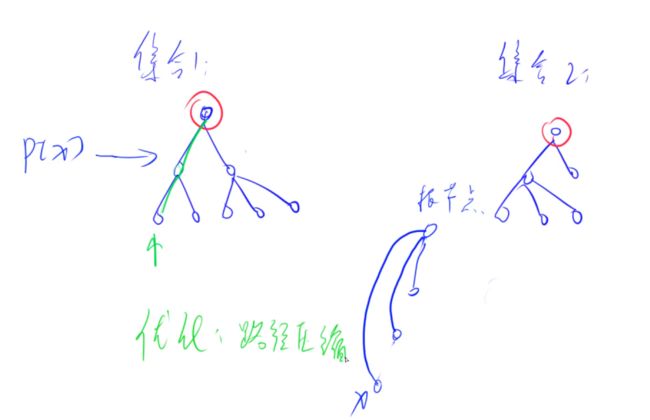
树的重心

https://www.acwing.com/problem/content/description/848/

#include 

using namespace std;

const int N = 1e5 + 10,M = N * 2;

int n,m;
// h[N]就是头节点,只是因为有多个链表,所以变为数组了 
int h[N],e[M],ne[M],idx;
bool st[N];
 
int ans = N; 

// 在a的链接表中,插入一个b 
void add(int a,int b){
	// 头插法 
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}

// 以u为根的子树中点的数量 
int dfs(int u){
	// 标记一下,已经被搜索过了 
	st[u] = true;
	// sum 当前子树的大小
	// res 每个连通块大小的最大值 
	int sum = 1,res = 0; 
	// 遍历连接表 
	for(int i = h[u];i != -1;i = ne[i]){
		// j 是相邻的点 
		int j = e[i];
		
		if(!st[j]) {
			// 与u相邻的点的子树的节点个数 
			int s = dfs(j);
			// 找出连通块的最大值 
			res = max(res,s);
			// 当前子树的大小,要加上当前点各个子节点为根的子树的大小
			sum += s;
		}
	}
	//  n - sum 是上面连通块的节点个数 
	res = max(res,n - sum);
	// res是连通块的最大值,我们要找到连通块最大的最小值 
	ans = min(res,ans);
	return sum;
}




int main(){
	cin >> n;
	// 都没有连接,-1表示尾节点 
	memset(h,-1,sizeof h);
	for(int i = 0;i < n;i++){
		int a,b;
		cin >> a >> b;
		add(a,b);
		add(b,a);
	}
	dfs(1);
	cout << ans << endl;
	return 0;
}

树与图的广度优先遍历

图中点的层次

https://www.acwing.com/problem/content/849/

#include  

using namespace std;

const int N = 1e5 + 10;

int n,m;
int h[N],e[N],ne[N],idx;
int d[N];
queue q;

void add(int a,int b){
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}

int bfs(){
	q.push(1);
	memset(d,-1,sizeof d);
	d[1] = 0;
	while(!q.empty()){
		int t = q.front();
		q.pop();
		for(int i = h[t];i != -1;i=ne[i]){
			int j = e[i];
			if(d[j] == -1){
				d[j] = d[t]+1;
				q.push(j);
			}
		}
	}
	return d[n];
}

int main(){
	cin >> n >> m;
	memset(h,-1,sizeof h);
	for(int i = 0;i < m;i++){
		int a,b;
		scanf("%d%d",&a,&b);
		add(a,b);
	}
	printf("%d\n",bfs());
	return 0;
}

拓扑排序

入度为零都可以作为起点

有向图的拓扑序列

https://www.acwing.com/problem/content/description/850/

#include 

using namespace std;

const int N = 1e5 + 10;

int n,m;

int h[N],e[N],ne[N],idx;

int q[N],d[N];

void add(int a,int b){
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}

bool topsort(){
    int hh = 0,tt =-1;
	for(int i = 1;i <= n;i++) {
		// 入度为0的点入队,队尾入队
		if(!d[i]) q[++tt] = i;
	}
	while(hh <= tt) {
	    // 队头出队
		int t = q[hh++];
		for(int i = h[t];i != -1;i = ne[i]){
			int j = e[i];
			// 删除i->j,就删除了j的入度
			d[j]--;
			// j 入队
			if(d[j] == 0) q[++tt]=j;
		}
	}
	// 队尾到n-1,表示全部加入,没有环 
	return tt == n -1;
}

int main(){
	cin >> n >> m;
	memset(h,-1,sizeof h);
	for(int i = 0;i < m;i++){
		int a,b;
		cin >> a >> b;
		add(a,b);
		// 入度 
		d[b]++;
	}
	if(topsort()){
		for(int i = 0;i < n;i++) {
			printf("%d ",q[i]);
		}
	}else puts("-1");
	
	return 0;
}

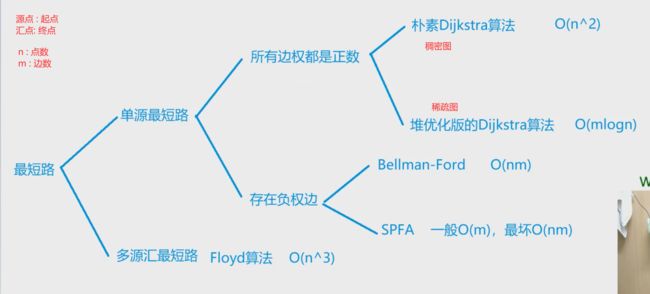
最短路问题

单源:只有一个起点

多源:有多个起点

稠密图:m~n^2 : 邻接矩阵,因为点多

稀疏图:m~n : 邻接表

朴素Dijkstra

Dijkstra求最短路 I

https://www.acwing.com/problem/content/851/

#include  

using namespace std;

const int N = 510;

int n,m;
// 稠密图,因为点多,用邻接矩阵 
int g[N][N];
int dist[N];
bool st[N];

int dijkstra(){
    // 初始化距离都为正无穷
	memset(dist,0x3f,sizeof dist);
	
	dist[1] = 0;
	
	// 迭代n次 
	for(int i = 0;i < n;i++){
		int t = -1;
		// 每次找S中距离最小的点 
		 for(int j = 1;j <= n;j++){
		 	//  t == -1 表示是第一个不在S中的点
			//  dist[t] > dist[j] 表示找到最小值 
		 	if(!st[j] && (t == -1 || dist[t] > dist[j])) t = j;
		}
		// t这个点用过了
	 	st[t] = true;
		 	
	 	for(int j = 1;j <= n;j++) {
	 		// g[t][j]	t到j的距离 
	 		// 更新距离
	 		dist[j] = min(dist[j],dist[t] + g[t][j]);
		}
	}
	if(dist[n] == 0x3f3f3f3f) return -1;
	return dist[n];
}

int main(){
	scanf("%d%d",&n,&m);
	
	// 初始化
	memset(g,0x3f,sizeof g);
	
	// 因为边的权值都是正的,所以存在自环也没关系,因为最短路不可能走自环 
	while(m--){
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		// 有重边,选最短的 
		g[a][b] = min(g[a][b],c);
	}
	
	int t = dijkstra();
	
	printf("%d\n",t);
	
	return 0;
}

堆优化Dijkstra

Dijkstra求最短路 II

https://www.acwing.com/problem/content/852/

#include 

using namespace std;

const int N = 2e5 + 10;

// 距离,编号 
typedef pair PII;

// 稀疏图,用邻接表,重边也无所谓,因为代码能保证选出最小的边 
int h[N],e[N],ne[N],w[N],idx;
int n,m;
int dist[N];
bool st[N];

void add(int a,int b,int c){ 
	e[idx] = b;
	ne[idx] = h[a];
	// 权重 
	w[idx] = c;
	h[a] = idx++;
}

int dijkstra(){
	memset(dist,0x3f,sizeof dist);
	dist[1] = 0;
	
	// 小根堆 
	priority_queue,greater> heap;
	heap.push({0,1});
	
	while(heap.size()){
		// 距离最小点 
		auto t = heap.top();
		heap.pop();
		
		// 编号 
		int ver = t.second;
		int distance = t.first;
		// 这个点之前出现过了 
		if(st[ver]) continue; 
		
		// 遍历ver的相邻的点 
		for(int i = h[ver];i != -1;i = ne[i]) {
			int j = e[i];
			// w[i]是j和ver之间的距离,插入就是这样插入的 
			// 如果通过ver的距离更小,就更新一下,虽然堆中会存在冗余 
			if(dist[j] > dist[ver] + w[i]) {
			    dist[j] = dist[ver] + w[i];
			    heap.push({dist[j],j});
			}
		}
		st[ver] = true;
	}
	if(dist[n] == 0x3f3f3f3f) return -1;
	else return dist[n];
}

int main(){
	scanf("%d%d",&n,&m);
	
	memset(h,-1,sizeof h);
	
	while(m--){
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
	}
	
	int t = dijkstra();
	
	printf("%d\n",t);
	
	return 0;
}

Bellman-Ford 算法

有边数限制的最短路

https://www.acwing.com/problem/content/description/855/

#include 

using namespace std;

const int N = 500 + 10,M = 10010;

int n,m;
int dist[N],backup[N];

struct Edge{
	int a,b,w;
}edges[N];

int bellman_ford(){
	memset(dist,0x3f;sizeof dist);
	// 不超过k条边,那么就只迭代k次 
	for(int i = 0;i < k;i++){
		// 可能会发生串联,那么需要备份
		// 这次迭代的结果影响了这次后面的迭代
		// 每次迭代的都使用上次跌带后的结果 
		memcpy(backup,dist,sizeof dist);
		// 遍历所有的边 
		for(int j = 0 ;j < m;++){
			int a = edges[j].a;
			int b = edges[j].b;
			int w = edges[j].w;
			// backup是上次迭代完之后的结果 
			dist[b] = min(dist[b],backup[a] + w);
		}
	}
	// 可能存在负权边 
	if(dist[n] > 0x3f3f3f3f/2) return -1;
	else return  dist[n];
}

int main(){
	scanf("%d%d%d",&a,&b,&c);
	
	for(int i = 0;i < m;i++){
		int a,b,w;
		scanf("%d%d%d",&a,&b,&w);
		// 存边 
		edges[i] = {a,b,w};
	}
	
	int t = bellman_ford();
	
	if(t == -1) puts("impossible");
	else printf("%d\n",t);
	
	return 0;
}

SPFA

Bellman-Ford算法优化:

dist[b] = min(dist[b],backup[a] + w);

只有a变小了,b才会变小,那么在这里进行BFS