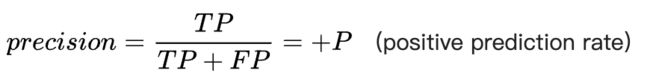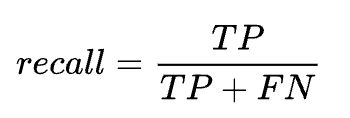一文读懂xgboost,lightgbm分类评价指标与阈值threshold的选取
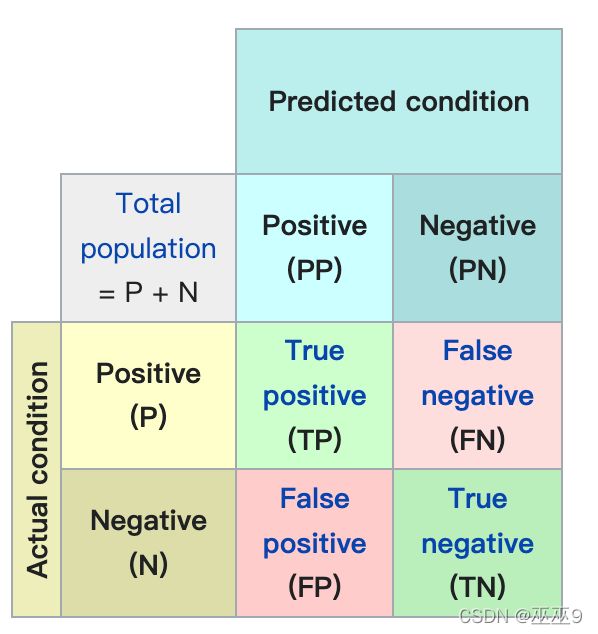
分类的评价指标主要有F-score(F-measure), recall, precision,ROC曲线,AUC曲线.其中涉及到混淆矩阵(confusion matrix), TN, TP, FN, FP.
事实上,这适用于所有的分类模型,并不局限于xgb,lgb。只是这两种模型分类效果尤为显著,因此本文以lgb作二分类为例,来应用这些评价指标,与展示threshold如何选取。
为了方便理解,我画了一张图:
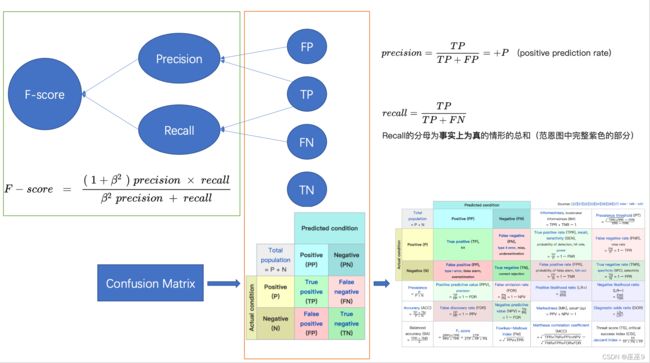
可以看出所有的指标,都是基于TP,FP,FN,TN计算公式的来。因此我们从底层开始理解,先需理解这四个就游刃有余了。(图中未提到的ROC曲线与AUC在后面。)
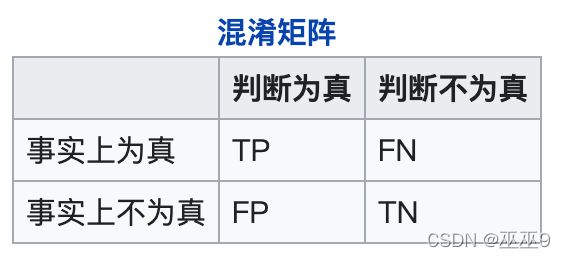
TP,FP,FN,TN & Confusion Matrix
前面的True/False修饰后面的Positive/Negative,后面的Positive/Negative是我们的方法的判断。
TP (true positive):我们的方法判断为真,这个判断是对的。即事实上为真,而且被我们的方法判断为真的情形。
FN (false negative):我们的方法判断为不真,这个判断是错的。即事实上为真,却未被我们的方法判断为不真的情形。
FP (false positive):我们的方法判断为真,这个判断是错的。即事实上不为真,却被我们的方法误判为真的情形。
TN (true negative):我们的方法判断为不真,这个判断是对的。即事实上不为真,而且被我们的方法判断成不为真的情形。
于此之外,还引申出许多其他的指标:
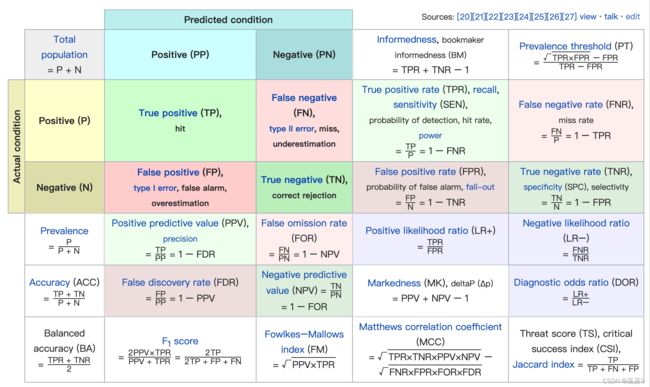
此处挑两个比较常用的(后面的ROC会用到)了解:
TPR & FPR
Precision & Recall
Precision,说白了,就是你的模型分类的准确性、精确度,即模型预测为真的里面,确实预测对的几个。
Precision的分母为两种判断为真的情形的总和。
解释:当辨识结果为FP的代价很高时,F-score应该着重此指标,亦即precision要很高。
例子:辨识电邮信箱里的垃圾邮件时,如果某封被误判成垃圾邮件(即FP)时,使用者可能就此错过重要的通知。
Recall,召回, 说白了,即 事实上是真的里面,模型预测对了几个
Recall的分母为事实上为真的情形的总和
解释:当辨识结果为FN的代价很高时,F-score应该着重此指标,亦即precall要很高。
举例:一个传染病诊断辨识系统中,如果某个传染病患者被误判成阴性(即FN),当地的社区的居民就落入被传染的高风险之中。
举例:真正犯罪的人当中,有多少比例的罪犯被抓到。或,一张照片当中,有多少人脸被侦测到。
通过以上的概念与解释,我们可以看出precision与recall是进行权衡的,F-而这种关系可以通过 β 调整更重视的部分。因此我们后面在选择threshold的时候,也需要根据实际的业务需求,通过更看重哪一部分,从而选择出需要的threshold.

以上面为例,那么如果警局倡导的是,尽量不要冤枉平民,那么就会青睐于选择下面严谨的做法;若是说了必须要多抓到犯人,那么肯定会选择上面雷厉风行的做法。
在实际业务中,threshold需根据产品、运营的拉齐,才可以决定。但同时也可以画出ROC曲线等,综合判断与折衷。
ROC曲线 & AUC 与代码实现
接收者操作特征曲线,或者叫ROC曲线(英语:Receiver operating characteristic curve),是一种坐标图式的分析工具,用于选择最佳的信号侦测模型、舍弃次佳的模型或者在同一模型中设置最佳阈值。
在做决策时,ROC分析能不受成本/效益的影响,给出客观中立的建议。(但实际业务中常常是有偏向性、指向性的)
ROC空间将伪阳性率(FPR)定义为 X 轴,真阳性率(TPR)定义为 Y 轴。给定一个二元分类模型和它的阈值,就能从所有样本的(阳性/阴性)真实值和预测值计算出一个 (X=FPR, Y=TPR) 坐标点。
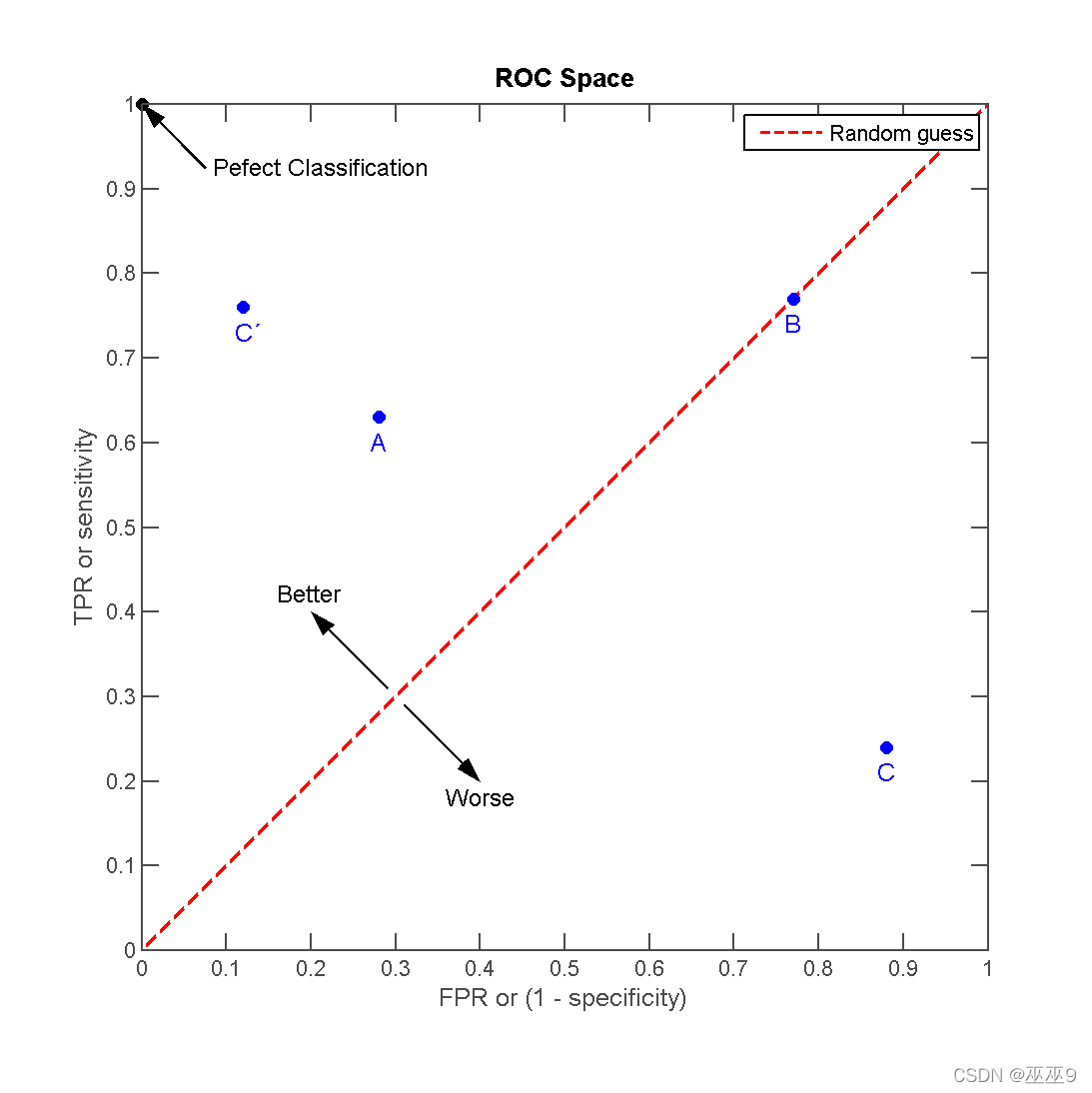
从 (0, 0) 到 (1,1) 的对角线将ROC空间划分为左上/右下两个区域,在这条线的以上的点代表了一个好的分类结果(胜过随机分类),而在这条线以下的点代表了差的分类结果(劣于随机分类)。
离左上角越近的点预测(诊断)准确率越高。
同一个二元分类模型的阈值可能设置为高或低,每种阈值的设置会得出不同的FPR和TPR。
将同一模型每个阈值 的 (FPR, TPR) 坐标都画在ROC空间里,就成为特定模型的ROC曲线。
代码实现:
from sklearn import metrics
import lightgbm as lgb
import matplotlib.pyplot as plt
import seaborn as sns
from numpy import sqrt, argmax
from sklearn import metrics
from matplotlib import pyplot
from sklearn.metrics import precision_recall_curve
fpr, tpr, thresholds = metrics.roc_curve(y_test, pred_test)
# calculate the g-mean for each threshold
gmeans = sqrt(tpr * (1-fpr))
# locate the index of the largest g-mean
ix = argmax(gmeans)
print('Best Threshold=%f, G-Mean=%.3f' % (thresholds[ix], gmeans[ix]))
# plot the roc curve for the model
pyplot.plot([0,1], [0,1], linestyle='--', label='No Skill')
pyplot.plot(fpr, tpr, marker='.', label='Lgbm')
pyplot.scatter(fpr[ix], tpr[ix], marker='o', color='black', label='Best')
# axis labels
pyplot.xlabel('False Positive Rate')
pyplot.ylabel('True Positive Rate')
pyplot.legend()
# show the plot
pyplot.show()
output: 图中小黑点是预测最佳的点(最靠近左上方)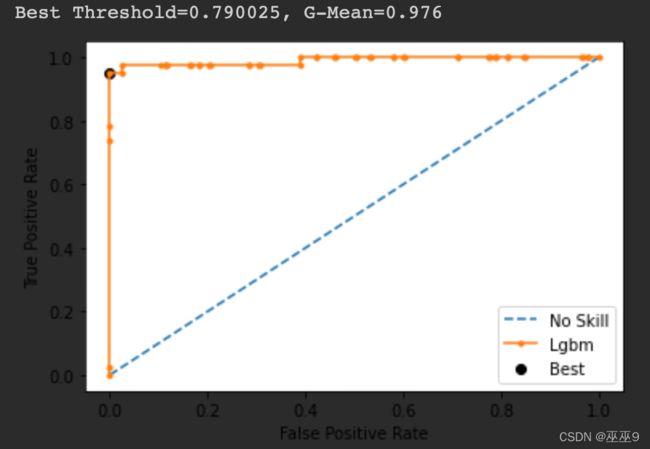

理解ROC曲线,AUC就迎刃而解了。
AUC就是ROC曲线下面的面积(Area under the Curve of ROC (AUC ROC))
AUC必在0~1之间,AUC值越大的分类器,正确率越高。
PR曲线与代码实现
from sklearn.metrics import precision_recall_curve
# calculate pr-curve
precision, recall, thresholds = precision_recall_curve(y_test, pred_test)
# convert to f score
fscore = (2 * precision * recall) / (precision + recall)
# locate the index of the largest f score
ix = argmax(fscore)
print('Best Threshold=%f, F-Score=%.3f' % (thresholds[ix], fscore[ix]))
# plot the roc curve for the model
no_skill = len(y_test[y_test==1]) / len(y_test)
pyplot.plot([0,1], [no_skill,no_skill], linestyle='--', label='No Skill')
pyplot.plot(recall, precision, marker='.', label='Lgbm')
pyplot.scatter(recall[ix], precision[ix], marker='o', color='black', label='Best')
# axis labels
pyplot.xlabel('Recall')
pyplot.ylabel('Precision')
pyplot.legend()
# show the plot
pyplot.show()
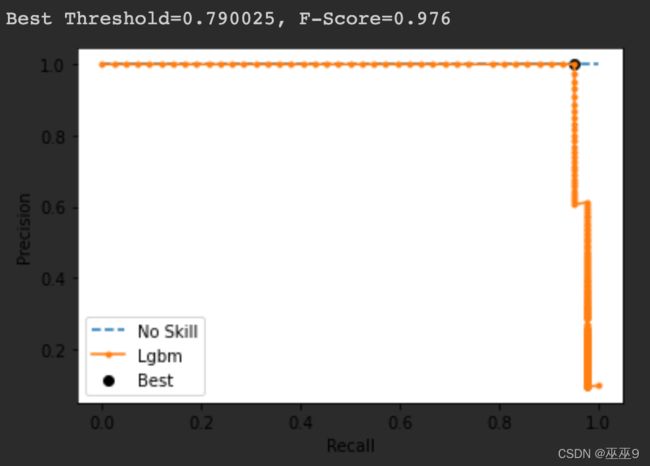
具体来说,threshold的选择还是需要参照PR曲线、ROC曲线、业务实际需求综合选择。
Reference:https://en.wikipedia.org/wiki/Confusion_matrixhttps://zh.wikipedia.org/wiki/F-scorehttps://zh.wikipedia.org/wiki/ROC%E6%9B%B2%E7%BA%BF