[论文阅读] Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts（MMoE模型）

[论文阅读] Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts

Abstract

基于神经网络的多任务学习在日常生活中应用广泛。但是，常用的多任务模型的预测质量对任务之间的关系很敏感。
本文提出的MMoE模型可以从数据中对任务关系进行建模，通过在所有任务共享专家子模型，使得专家混合结构适应多任务学习，同时优化每个任务的门控网络。

Introduction

背景：对于推荐系统，举个例子：当推荐给用户看的电影时，希望用户不仅可以购买和看这个电影，而且希望用户看完之后能够回来去看或者购买更多的电影。也就是说，要创建模型同时预测用户的购买和评级。

现在的问题：许多基于DNN的多任务学习模型对诸如任务之间的数据分布差异和关系等因素敏感 。来自任务差异的固有冲突实际上可能会损害至少某些任务的预测，尤其是当模型参数在所有任务之间广泛共享时。

前人的工作及问题1：之前的工作是为每个任务假设特定的数据生成过程以衡量任务之间的差异，然后提出不同的建议。但是，实际任务有着更复杂的数据模式，因此难以测量差异。

前人的工作及问题2：最近的工作提出了无需依靠显式的任务差异度量，但是这些技术通常涉及添加更多的模型参数，这可能会损害模型质量，在实际生产中消耗也很高。

MMoE：本文受到专家混合模型（MoE）的启发，显式地对任务关系建模，并学习特定于任务的功能以利用共享表示。它允许自动分配参数以捕获共享的任务信息或特定于任务的信息，从而避免了每个任务添加许多新参数的需要。
MMoE的主干建立在最常用的共享底部多任务深度神经网络结构上 ，共享底部模型如下图所示。其中在输入层之后的几个底层在所有任务中共享，然后每个任务在底部表示的顶部都有一个单独的网络 “塔”。

如下图所示，该模型没有一个底层网络被所有任务共享，而是有一组底层网络，每个底层网络被称为专家。本文中每个专家都是一个前馈网络。然后引入门控网络，采用输入功能并输出softmax门，以不同的权重组装专家，从而使不同的任务以不同的方式利用专家。然后将组装的专家的结果传递到特定于任务的塔式网络中。这样，针对不同任务的门控网络可以学习专家组装的不同混合模式，从而捕获任务关系。

实验设计：使用皮尔逊相关性来测量和控制任务相关性。我们使用两个合成回归任务，并使用正弦函数作为数据生成机制来引入非线性。优于基线方法，尤其在任务相关性比较低的情况下。实验中还发现MMoE更易于训练，这与最近的发现有关，即调制和门控机制可以提高训练非凸深度神经网络的训练能力。
贡献：

1. 提出了一种新颖的多门专家混合模型，该模型对任务关系进行了显式建模。通过调制和门控网络，我们的模型会自动调整建模共享信息与建模特定于任务的信息之间的参数化。
2. 使用合成数据进行控制实验。我们报告了任务相关性如何影响多任务学习中的训练动态，以及MMoE如何提高模型表达力和可训练性。
3. 在基准数据和现实环境中进行了实验，表明了有效性。

Related Work

Multi-task Learning in DNNs

多任务模型可以学习不同任务之间的共性和差异。这样可以提高每个任务的效率和模型质量。Caruana提出了一种多任务模型，该模型具有共享底部模型结构，并且是跨任务共享。这种结构降低了过拟合风险，但可能会造成优化冲突。

任务相关性如何影响模型质量？先前的工作使用了合成数据生成并操纵了不同类型的任务相关性，以评估多任务模型的有效性。

现在的工作主要是想办法具有更多的特定于任务的参数（相比于共享底层模型），导致任务差异导致更新参数发生冲突时有更好的性能。更多的任务意味着更多的参数，这不太好，并且在大规模模型中可能不太有效。

Ensemble of Subnets & Mixture of Experts

将一些最新发现（参数调制和集成方法）用于多任务学习的任务关系建模中。

Eigen 和Shazeer等人将专家混合模型转换为基本构建块 (MoE层)，并将它们堆叠在DNN中。MoE层根据层在训练时间和服务时间的输入选择子网 (专家)。因此，该模型不仅在建模方面更强大，而且通过将稀疏性引入门控网络来降低计算成本。

Multi-task Learning Applications

在多语言机器翻译任务上，在共享模型参数的情况下，通过与训练数据量大的任务联合学习，可以改善训练数据有限的翻译任务 。

多任务学习有助于提供上下文感知的推荐。

PRELIMINARY

Shared-bottom Multi-task Model

如图（a）所示，给定K个任务，该模型由一个共享底部网络（表示为$f$）和K个塔网络$h^k$组成。共享底部网络接输入层，塔网络接共享底部网络。对于任务K，模型课表示为：

Synthetic Data Generation

多任务学习模型的性能在很大程度上取决于数据中固有的任务相关性。然而，研究实际应用中的数据相关性很难，因为不能轻易改变相关性。因此，首先使用合成数据来进行研究。
生成两个回归任务，并使用两个任务的Person相关性作为量化指标。由于是DNN，因此将回归模型设置为正弦函数的组合。数据如下：

1. 给定输入特征维数d，我们生成两个正交的单位向量$u_1,u_2\in R^d$
   
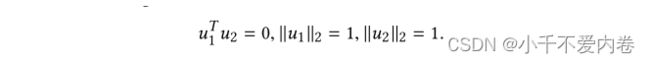
2. 给定比例常数c和相关分数−1≤p≤1，生成两个权重向量$w_1，w_2$使得
   
3. 从N (0,1) 随机采样一个输入数据点x ∈ Rd及其每个元素。
4. 为两个回归任务生成两个labels。$y_1，y_2$如下:
   
5. 重复 (3) 和 (4)，直到产生足够的数据。

生成具有给定标签Person相关性并不容易。相反，通过操纵权重向量$w_1，w_2$的余弦相似性，然后测量标签的Person相关性。
在线性条件下，$y_1，y_2$的相关性正好为p。非线性情况下也是呈正相关的。

Impact of Task Relatedness

为了验证低任务相关性会损害基线多任务模型设置中的模型质量，进行了如下控制实验。

1. 给定任务相关分数列表，为每个分数生成合成数据集；
2. 分别在每个数据集上训练一个共享底部多任务模型，同时控制所有模型和训练超参数保持不变；
3. 用独立生成的数据集重复步骤 (1) 和 (2) 数百次，但控制任务相关分数的列表和超参数相同；
4. 计算每个任务相关分数的模型的平均性能。

结果：

任务之间的相关性越高，效果越好；相关性越低，效果越差。
思考：为什么会出现这种情况？因为多任务网络是共享底层网络的，如果任务相似，则底层网络的参数可以更好的适应这些任务；如果任务不相似，则底层网络的参数在优化过程中可能会更大概率上产生冲突，导致不能够更好适应这些任务，导致结果变差。

MODELING APPROACHES

Mixture-of-Experts

最初的MoE模型可以表述为：

其中${\sum }_{i=1}^{n}g(x{)}_i=1$，输出的第i个g (x) 表示专家$f_i$的概率

在这里，$f_i$，i = 1，…，n是n个专家网络，而 g 代表一个门控网络，它集合了所有专家的结果。更具体地，门控网络g基于输入在n个专家上产生分布，并且最终输出是所有专家的输出的加权和。
MoELayer：MoE层具有与MoE模型相同的结构，但接受前一层的输出作为输入并输出到连续层。然后以端到端的方式训练整个模型。目的是实现条件计算，在每个示例的基础上只有部分网络是活动的。对于每个输入示例，模型只能通过以输入为条件的门控网络选择专家的子集。

Multi-gate Mixture-of-Experts

本文的模型的核心思想是将共享底部网络$f$替换为刚刚说的MoE层。而且为每个任务k添加一个单独的门控网络$g^k$。任务K的输出为：

我们的实现由具有ReLU激活的相同多层感知器组成。门控网络只是具有softmax层的输入的线性转换:

其中，$W_{gk}\in R^{n\times d}$是一个可训练的矩阵，n为专家系统的个数，d是输入数据维度。

每个门控网络选择自己所需要的专家子集。这使得参数共享更灵活。MMoE能够通过确定由不同门产生的分离如何彼此重叠来以复杂的方式对任务关系进行建模。多门是有用的，为了对比，搞了一个一个门的MoE模型，如下图。

MMOE ON SYNTHETIC DATA

MMoE是否确实可以更好处理任务相关性较小的情况。同样使用合成数据进行实验。并证明了MMoE更容易被训练。

Performance on Data with Different Task Correlations

使用MMoE模型和两个基线模型重复之前的实验：共享底部模型和OMoE模型。
结果：

1. 对于所有的模型，相关性较高的数据上的性能好于相关性低的数据的性能。
2. MMoE模型在具有不同相关性的数据上的性能之间的差距比OMoE模型和共享底部模型要小得多。

Trainability

可训练性：模型在超参数设置和模型初始化范围内的鲁棒性。

方法：在每个设置下重复实验多次。每次从相同的分布但是不同的随机种子生成数据时，模型的初始化也不同。

注意，MMoE和OMoE之间的唯一区别在于是否存在多门结构。这验证了多门结构在解决由任务差异冲突引起的不良局部最小值方面的有用性。

REAL DATA EXPERIMENTS

在真实数据集上进行实验，以验证方法的有效性。

Baseline Methods

除了共享底部模型，还与几种最先进的多任务深度神经网络模型对比。

L2-Constrained：此方法是针对具有两个任务的跨语言问题而设计的。在这种方法中，用于不同任务的参数由L2约束软共享。给定$y_k$作为任务k的地面真值标签，k ∈ 1,2，任务k的预测表示为
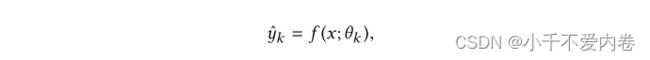目标函数：

α 是超参数，该方法以 α 的大小对任务相关性进行建模

Cross-Stitch：该方法通过引入 “十字绣” 单元在两个任务之间共享知识。十字绣单元从任务1和2中获取分离的隐藏层x1和x2的输入，并通过以下公式分别输出〜xi 1和〜xi 2:

Tensor-Factorization：权重被建模为张量，张量分解方法用于跨任务的参数共享。给定输入隐藏层大小m，输出隐藏层大小n和任务数k，权重W (即m × n × k张量) 由下式导出:

Hyper-Parameter Tuning

使用了超参数调节器，在数据集中搜索最佳超参数。

Census-income Data

公开数据集上的实验结果：

Large-scale Content Recommendation

具体地，给定用户当前消费物品的行为，该推荐系统的目标是向用户显示接下来要消费的相关物品的列表。

CONCLUSION

提出了一种新颖的多任务学习方法，多门MoE (MMoE)，该方法可以明确地学习从数据中建模任务关系。我们通过对合成数据的控制实验表明，所提出的方法可以更好地处理任务相关性较小的情况。与基线方法相比，MMoE更容易训练。通过在基准数据集和实际的大规模推荐系统上进行的实验，我们证明了所提出的方法在几种最先进的基线多任务学习模型上的成功。

实际机器学习生产系统中的另一个主要设计考虑因素是计算效率。。但是，由于门控网络通常重量轻并且专家网络在所有任务中共享，因此MMoE模型在很大程度上保留了计算优势。（MMoE的门控网络是轻量级的）