论文阅读：Colorful Image Colorization
目录
Contributions
Method
1、Objective Function
2、Class rebalancing
3、Class Probabilities to Point Estimates
Code
Results
1、Colorization results on 10k images in the ImageNet validation set
2、Colorization Turing Test.
3、Cross-Channel Encoding as Self-Supervised Feature Learning
论文名称：Colorful Image Colorization（2016 ECCV）
论文作者：Richard Zhang, Phillip Isola, Alexei A. Efros
下载地址：https://arxiv.org/pdf/1603.08511.pdf
论文网站（code）：http://richzhang.github.io/colorization/
参考理解：https://blog.csdn.net/Limonor/article/details/109078294
Contributions
Given a grayscale photograph as input, this paper attacks the problem of automatic image colorization. First, we embrace the underlying uncertainty of the problem by posing it as a classification task and use class-rebalancing at training time to increase the diversity of colors in the result. Second, we evaluate our algorithm using a “colorization Turing test”, asking human participants to choose between a generated and ground truth color image, which is potentially applicable to other image synthesis tasks. Moreover, we show that colorization can be a powerful pretext task for self-supervised feature learning, acting as a cross-channel encoder. This approach results in state-of-the-art performance on several feature learning benchmarks.
Method
We train a CNN to map from a grayscale input to a distribution over quantized color value outputs. Each conv layer refers to a block of 2 or 3 repeated conv and ReLU layers, followed by a BatchNorm layer. The net has no pool layers. All changes in resolution are achieved through spatial downsampling or upsampling between conv blocks.
1、Objective Function
Given an input lightness (L) channel 
, our objective is to learn a mapping 
to the two associated color channels (a, b) 
, where H,W are image dimensions.
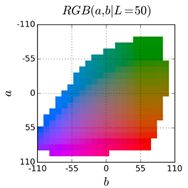
Then, we treat the problem as multinomial classification. We quantize the ab output space into bins with grid size 10 and keep the Q=313 values which are in-gamut, as shown in Figure. For a given input X, we learn a mapping 
to a probability distribution over possible color
, where Q is the number of quantized ab values.
To compare predicted 
against ground truth, we define function 
which converts ground truth color Y to vector Z, using a soft-encoding scheme. We then use multinomial cross entropy loss Lcl(⋅,⋅), defined as:
where v(⋅) is a weighting term that can be used to rebalance the loss based on color-class rarity. Finally, we map probability distribution 
to color values 
with function 
.
2、Class rebalancing
The distribution of ab values in natural images is strongly biased towards values with low ab values, due to the appearance of backgrounds such as clouds, pavement, dirt, and walls. We account for the class-imbalance problem by reweighting the loss of each pixel at train time based on the pixel color rarity.
3、Class Probabilities to Point Estimates
Finally, we define 
, which maps the predicted distribution 
to point estimate 
in ab space. We interpolate by re-adjusting the temperature T of the softmax distribution, and taking the mean of the result. We draw inspiration from the simulated annealing technique [33], and thus refer to the operation as taking the annealed-mean of the distribution:
Our final system 
is the composition of CNN 
, which produces a predicted distribution over all pixels, and the annealed-mean operation 
, which produces a final prediction. The system is not quite end-to-end trainable, but note that the mapping 
operates on each pixel independently, with a single parameter, and can be implemented as part of a feed-forward pass of the CNN.
Code
class ECCVGenerator(BaseColor):
def __init__(self, norm_layer=nn.BatchNorm2d):
super(ECCVGenerator, self).__init__()
model1=[nn.Conv2d(1, 64, kernel_size=3, stride=1, padding=1, bias=True),]
model1+=[nn.ReLU(True),]
model1+=[nn.Conv2d(64, 64, kernel_size=3, stride=2, padding=1, bias=True),]
model1+=[nn.ReLU(True),]
model1+=[norm_layer(64),]
model2=[nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1, bias=True),]
model2+=[nn.ReLU(True),]
model2+=[nn.Conv2d(128, 128, kernel_size=3, stride=2, padding=1, bias=True),]
model2+=[nn.ReLU(True),]
model2+=[norm_layer(128),]
model3=[nn.Conv2d(128, 256, kernel_size=3, stride=1, padding=1, bias=True),]
model3+=[nn.ReLU(True),]
model3+=[nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1, bias=True),]
model3+=[nn.ReLU(True),]
model3+=[nn.Conv2d(256, 256, kernel_size=3, stride=2, padding=1, bias=True),]
model3+=[nn.ReLU(True),]
model3+=[norm_layer(256),]
model4=[nn.Conv2d(256, 512, kernel_size=3, stride=1, padding=1, bias=True),]
model4+=[nn.ReLU(True),]
model4+=[nn.Conv2d(512, 512, kernel_size=3, stride=1, padding=1, bias=True),]
model4+=[nn.ReLU(True),]
model4+=[nn.Conv2d(512, 512, kernel_size=3, stride=1, padding=1, bias=True),]
model4+=[nn.ReLU(True),]
model4+=[norm_layer(512),]
model5=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
model5+=[nn.ReLU(True),]
model5+=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
model5+=[nn.ReLU(True),]
model5+=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
model5+=[nn.ReLU(True),]
model5+=[norm_layer(512),]
model6=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
model6+=[nn.ReLU(True),]
model6+=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
model6+=[nn.ReLU(True),]
model6+=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
model6+=[nn.ReLU(True),]
model6+=[norm_layer(512),]
model7=[nn.Conv2d(512, 512, kernel_size=3, stride=1, padding=1, bias=True),]
model7+=[nn.ReLU(True),]
model7+=[nn.Conv2d(512, 512, kernel_size=3, stride=1, padding=1, bias=True),]
model7+=[nn.ReLU(True),]
model7+=[nn.Conv2d(512, 512, kernel_size=3, stride=1, padding=1, bias=True),]
model7+=[nn.ReLU(True),]
model7+=[norm_layer(512),]
model8=[nn.ConvTranspose2d(512, 256, kernel_size=4, stride=2, padding=1, bias=True),]
model8+=[nn.ReLU(True),]
model8+=[nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1, bias=True),]
model8+=[nn.ReLU(True),]
model8+=[nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1, bias=True),]
model8+=[nn.ReLU(True),]
model8+=[nn.Conv2d(256, 313, kernel_size=1, stride=1, padding=0, bias=True),]
self.model1 = nn.Sequential(*model1)
self.model2 = nn.Sequential(*model2)
self.model3 = nn.Sequential(*model3)
self.model4 = nn.Sequential(*model4)
self.model5 = nn.Sequential(*model5)
self.model6 = nn.Sequential(*model6)
self.model7 = nn.Sequential(*model7)
self.model8 = nn.Sequential(*model8)
self.softmax = nn.Softmax(dim=1)
self.model_out = nn.Conv2d(313, 2, kernel_size=1, padding=0, dilation=1, stride=1, bias=False)
self.upsample4 = nn.Upsample(scale_factor=4, mode='bilinear')
def forward(self, input_l):
conv1_2 = self.model1(self.normalize_l(input_l))
conv2_2 = self.model2(conv1_2)
conv3_3 = self.model3(conv2_2)
conv4_3 = self.model4(conv3_3)
conv5_3 = self.model5(conv4_3)
conv6_3 = self.model6(conv5_3)
conv7_3 = self.model7(conv6_3)
conv8_3 = self.model8(conv7_3)
out_reg = self.model_out(self.softmax(conv8_3))
return self.unnormalize_ab(self.upsample4(out_reg))
Results
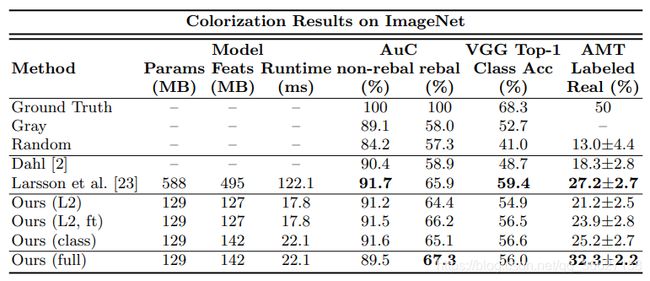
1、Colorization results on 10k images in the ImageNet validation set
2、Colorization Turing Test.
Images sorted by how often AMT participants chose our algorithm’s colorization over the ground truth.
3、Cross-Channel Encoding as Self-Supervised Feature Learning
