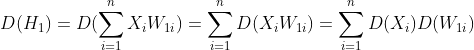给深层网络做参数初始化的门道及其原理
1 前言
神经网络的参数学习是一个非凸优化问题,当使用梯度下降法优化网络参数时,参数初始值的选取十分关键。如果参数的初始值不恰当,轻则影响网络的优化效率和泛化能力,重则导致梯度爆炸或消失。
参数初始化的方式通常有三种:预训练初始化、随机初始化、固定值初始化。预训练初始化是指用已经训练好的模型参数来初始化待训练网络的参数。固定值初始化是指用一个固定值来初始化参数。随机初始化是指用一个随机值来初始化参数。这个随机值可以没有规律,也可以让其服从某个分布。
实践中,随机初始化是较常用的权值初始化方法。现有的深度学习理论中提出了不少随机初始化方法。然而,如果采用不恰当的随机初始化方法,网络训练时可能会出现梯度爆炸或消失。那么,面对诸多的随机初始化方法,该如何选择呢。本文将对随机初始化方法的底层逻辑进行深入剖析,以便能在理解的基础上灵活运用随机初始化方法。
2 权值初始化不当导致梯度爆炸或消失的原因分析
首先用一个全连接网络的代码实例来看看,当用标准正态分布随机初始化各层参数时,各层输出数据标准差的变化。
class MLP(nn.Module):
def __init__(self, neural_num, layers):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.neural_num = neural_num
def forward(self, x):
for (i, linear) in enumerate(self.linears):
x = linear(x)
print("layer:{}, std:{}".format(i, x.std()))
if torch.isnan(x.std()):
print("output is nan in {} layers".format(i))
break
return x
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
nn.init.normal_(m.weight.data)if __name__ == '__main__':
layer_nums = 50
neural_nums = 256
batch_size = 16
net = MLP(neural_nums, layer_nums)
net.initialize()
inputs = torch.randn((batch_size, neural_nums))
output = net(inputs)
print(output)上面代码构建了一个50层的全连接网络,每层有256个神经元。为了简化问题,没有使用激活函数。MLP类中的Forward方法中加了条件判断语句,如果隐层的标准差为nan,则打印输出所在层号,并退出循环。程序运行结果如下图所示。
上图显示,网络第30层输出的标准差超出精度可表示范围。我们还发现,标准差的值逐层指数级增大。
为什么隐层数据的标准差会逐层增大?标准差增大是否会导致梯度爆炸?对于这两个问题,还必须从公式推导中来分析。
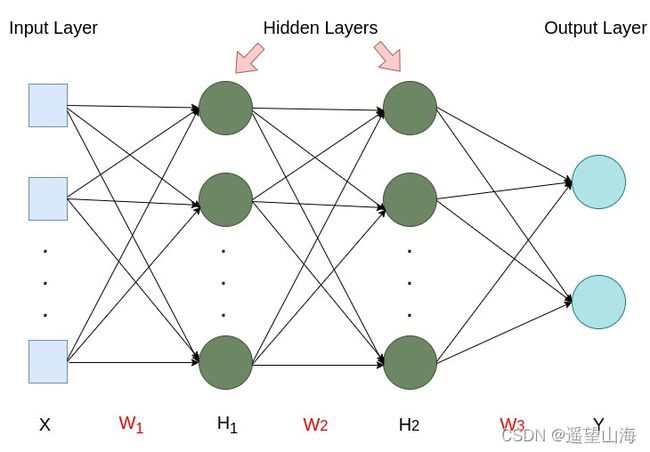
上图为四层全连接网络,由输入层、两个隐藏层和输出层组成。其中![]() 为输入样本,
为输入样本,![]() 、
、![]() 、
、![]() 为权值参数,
为权值参数,![]() 、
、![]() 为隐层,
为隐层,![]() 为网络输出。为简化问题,先不使用激活函数。
为网络输出。为简化问题,先不使用激活函数。
下面从公式推导中分析一下标准差逐层变大的原因。设每层神经元的个数均为![]() ,
,![]() 为第一个隐层第一个神经元
为第一个隐层第一个神经元![]() 的方差,则
的方差,则
设![]() 与
与![]() 相互独立、
相互独立、![]() 与
与![]() 相互独立,且
相互独立,且![]() 与
与![]() ,
,![]() ,
,![]() ,则有,
,则有,
设随机变量的期望为0,方差为1,即![]() ,
,![]() ,代入公式(1)得,
,代入公式(1)得,
所以,
![]()
其中,![]() 表示
表示![]() 的标准差. 同理可推得
的标准差. 同理可推得![]() 的方差和标准差,如下方公式所示。
的方差和标准差,如下方公式所示。
![]()
由上述推导可知,各层数据的标准差逐层增大![]() 倍。
倍。
下面我们来分析一下,标准差变大导致梯度爆炸的原因。
设损失函数为![]() ,则由链式求导法则,梯度
,则由链式求导法则,梯度![]() 可由下式表示,
可由下式表示,
将![]() 代入公式(4)得,
代入公式(4)得,
由公式(5)可知,当![]() 时,
时,![]() 。当
。当![]() 时,
时,![]() 。也就是说,当隐层数据尺度波动很大时,梯度也会随之有很大的波动。
。也就是说,当隐层数据尺度波动很大时,梯度也会随之有很大的波动。
3 如何避免梯度爆炸
由公式(2)、公式(3)可知,当![]() 时,隐层数据的方差逐层增大
时,隐层数据的方差逐层增大![]() 倍。而隐层数据方差增大是导致梯度爆炸的主要原因。为了避免这种情况发生,我们希望能将每个隐层的方差始终保持在1附近,即令
倍。而隐层数据方差增大是导致梯度爆炸的主要原因。为了避免这种情况发生,我们希望能将每个隐层的方差始终保持在1附近,即令![]() . 我们不妨令
. 我们不妨令![]() ,则有
,则有
所以,
由公式(7)可知,如果要让每个隐层![]() 的方差始终保持为1,就要使每层权值
的方差始终保持为1,就要使每层权值![]() 的方差为
的方差为![]() 。
。
也就是说,当我们用标准差为![]() 对每层权值参数进行随机初始化时,可以避免隐层标准差逐层增大的情况发生,从而避免由此带来的梯度爆炸。
对每层权值参数进行随机初始化时,可以避免隐层标准差逐层增大的情况发生,从而避免由此带来的梯度爆炸。
4 Xavier初始化方法与Kaiming初始化方法
- Xavier初始化方法
上述推导过程是在不考虑激活函数的情况下进行的。那么,如果我们使用激活函数,按照上述方法对权值参数以![]() 的方差进行随机初始化,经过激活函数后,方差还会始终保持为1吗?
的方差进行随机初始化,经过激活函数后,方差还会始终保持为1吗?
本人为此采用tanh激活函数进行了代码实验,发现各层输出的标准差不再保持不变,而是逐层递减。也就是说,前一层的标准差是后一层标准差的![]() 倍,
倍,![]() 。这里的
。这里的![]() 可以理解为tanh的增益。它是指当前层的标准差与当上一层标准差之比,可用下方公式表示,
可以理解为tanh的增益。它是指当前层的标准差与当上一层标准差之比,可用下方公式表示,
在pytorch中,可以使用torch.nn.init.calculate_gain()函数来获得激活函数的增益。
针对sigmoid、tanh这样的饱和激活函数,Xavier等人在论文Understanding the difficulty of training deep feedforward neural networks中,提出了有效的权值初始化方法,以使每层输出的标准差尺度保持一致。
以均匀分布为例,![]() ,Xavier初始化方法大致可分两个步骤:1) 求分布中的参数
,Xavier初始化方法大致可分两个步骤:1) 求分布中的参数![]() ;2) 用激活函数的增益gain乘以
;2) 用激活函数的增益gain乘以![]() ,得到在使用激活函数后,均匀分布
,得到在使用激活函数后,均匀分布![]() 中的参数
中的参数![]() ,
,![]() ,
,![]() .
.
(Ⅰ) 求![]()
根据Xavier论文中的推导,在不考虑激活函数的情况下,要使各层输出的标准差保持在1附近,权值参数![]() 的方差必须满足下式,
的方差必须满足下式,
![]() 表示输入神经个数,
表示输入神经个数,![]() 表示输出神经元个数。
表示输出神经元个数。
又,![]() ,所以
,所以
由公式(8)和公式(9)可得,
(Ⅱ) 求![]()
求出![]() 后,就可以用pytorch中的均匀分布函数来对权值参数进行初始化:
后,就可以用pytorch中的均匀分布函数来对权值参数进行初始化:
torch.nn.init.uniform_(weight, -a, a)
上述步骤是通过手动求![]() 的方式来实现X
的方式来实现Xavier初始化方法,其实pytorch有提供均匀分布的Xavier初始化函数:
torch.nn.init.xavier_uniform_(tensor, gain=1.0)
pytorch还提供了正态分布的Xavier初始化函数:
torch.nn.init.xavier_normal_(tensor, gain=1.0)
在网络模型中,如果激活函数使用的是sigmoid或tanh,不妨可以采用Xavier方法来初始化权值参数。
- Kaiming初始化方法
当采用ReLU激活函数时,Xavier初始化方法失效了。为了解决此问题,He等人在论文Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification中提出了一种方法,其推导结论如下,
其中![]() 为输入层神经元个数,
为输入层神经元个数,![]() 为LeakyReLU负半轴斜率。
为LeakyReLU负半轴斜率。
Kaiming初始化方法中,最终标准差的计算不再需要乘以ReLU激活函数的增益,直接根据ReLU的类型,用上述公式求方差即可。如果用的是ReLU,用公式(10)求方差。如果用的是LeakyReLU,则用公式(11)求方差。
例如,在网络模型中采用LeakyReLU激活函数,想用Kaiming方法初始化权重参数![]() ,使得
,使得![]() 服从正态分布,那么只要使正态分布中的方差等于公式(11),期望为0,就可以让各层输出的标准差尺度基本保持不变,
服从正态分布,那么只要使正态分布中的方差等于公式(11),期望为0,就可以让各层输出的标准差尺度基本保持不变,![]() 的分布如下方公式所示。
的分布如下方公式所示。
我们可以用pytorch中的正态分布函数实现上述的初始化:
torch.nn.init.normal_(mean=0, std=![]() )
)
不过,可以不用手动实现Kaiming初始化方法,在pytorch中有提供Kaiming初始化函数。
pytorch提供了均匀分布的Kaiming初始化函数和正态分布的Kaiming初始化函数:
torch.nn.init.kaiming_uniform_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
torch.nn.init.kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
在网络模型中,如果激活函数使用的是ReLU或LeakyReLU,不妨可以采用Kaiming初始化方法。
5 总结
避免梯度爆炸和梯度消失的基本思路是让每层输出的标准差始终保持为1。上述方法的基本思路是通过改变权值参数的标准差来使得每层输出标准差保持为1。
在公式(6)的推导中,还有一个前提条件是![]() ,它是指当前层输入的方差等于1。这可以通过把每层的输出都归一化为标准正态分布来实现。
,它是指当前层输入的方差等于1。这可以通过把每层的输出都归一化为标准正态分布来实现。
Xavier方法与Kaiming方法都是基于方差缩放的参数初始方法。在深度学习理论中,还有许多其它方法,在构建深层网络模型时,可根据激活函数的特性来选择合适的权值初始化方法。
[参考文献]
[1] Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks[C]//Proceedings of the thirteenth international conference on artificial intelligence and statistics. JMLR Workshop and Conference Proceedings, 2010: 249-256.
[2] He K, Zhang X, Ren S, et al. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification[C]//Proceedings of the IEEE international conference on computer vision. 2015: 1026-1034.
[3] 邱锡鹏. 神经网络与深度学习[M]. 北京: 机械工业出版社, 2021.


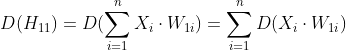
![=\sum_{i=1}^{n}[D(X_{i})\cdot D(W_{1i})+D(X_{i})\cdot E^{2}(W_{1i})+D(W_{1i})\cdot E^{2}(X_{i})]](http://img.e-com-net.com/image/info8/fcd24bdb3a384abe9e9d9b6b3d343125.gif)
![D(H_{11})=\sum_{i=1}^{n}[D(X_{i})\cdot D(W_{1i})+D(X_{i})\cdot 0+D(W_{1i})\cdot 0]](http://img.e-com-net.com/image/info8/c17b33fee54947f2b45d57283e91ea7f.gif)
![=\sum_{i=1}^{n}[1\cdot 1]=n\cdot 1\cdot 1=n](http://img.e-com-net.com/image/info8/7d41936b6d524caa966de50210118f11.gif)