python线性回归实现(简易版+原理版)
线性回归模型样例:
假设1:影响房价的关键因素是卧室个数和居住面积等因素,即为x1, x2, x3
假设2:成交价的关键因素的加权和
y=w1x1 + w2x2 +w3x3 +b
这里我们通常将w理解为权重,b理解为偏差量(标量)
我们可以简单的把线性模型理解为一个单层的网络模型,如下图所示

接下来我们直接在python上演示
原理版实现
首先按照给定要求生成(y = Xw + b +n) [X为数据,w为权重,b为偏差,n为噪声]
给定 w = [2,-3.4], b=4.2
# 根据带有噪声的线性模型构造一个人造数据集。我们使用线性模型参数
# w , b 和噪声d生成数据集及其标签
def synthetic_data(w, b, num_examples):
X = torch.normal(0,1,(num_examples, len(w))) ###生成mean=0, std=1, size=(num_examples, len(w)) 的向量
y = torch.matmul(X,w) + b
y += torch.normal(0, 0.01, y.shape)
return X, y.reshape((-1,1)) ### 将Y 转换为列向量
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
print('features:', features[0], '\nlabel:', labels[0])
plt.figure()
plt.scatter(features[:, 1].detach().numpy(),
labels.detach().numpy(),1)
plt.show()
torch.normal(mean,std,size) #生成高斯分布的数据
torch.matmul(x,y) #x*y注意最后生成的y必须转换成列向量(表示每一个数值)
定义好数据生成函数后,我们将X,与y定义为features,与labels
我们可以查看一下生成的数据图,我们可以发现数据分布满足线性
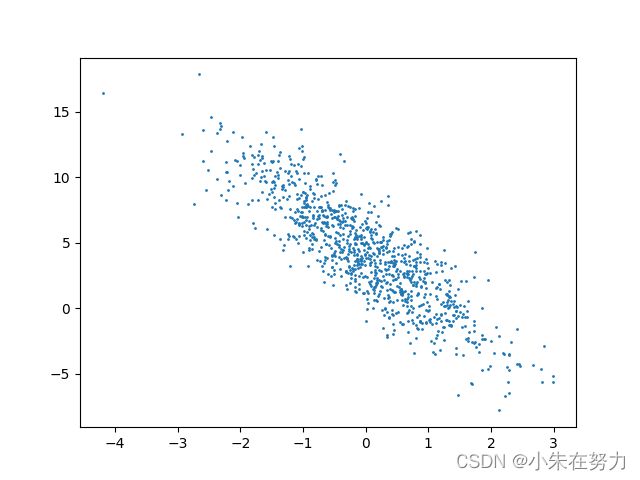
定义好数据后,我们需要定义接受数据的函数,其中包含batch_size批次量,特征features,标签labels
代码如下图所示
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) ## 打乱下标
for i in range(0, num_examples, batch_size):
batch_indices = torch.tensor(
indices[i:min(i + batch_size, num_examples)])
yield features[batch_indices], labels[batch_indices]
batch_size = 10
for X, y in data_iter(batch_size,features, labels):
print(X, '\n',y )
break
需要注意的是,因为数据要参加训练所以必须打乱,即random.shuffle,这里我们打印我们读取到的数据
可以得到数据格式为 (10,2)
tensor([[-0.9799, -0.5394],
[-0.1818, 0.4705],
[-1.0967, -2.5218],
[-1.4719, 0.4218],
[-0.7889, -1.4477],
[-0.2622, -0.1918],
[-1.1138, -0.8647],
[-0.5958, -0.3762],
[-1.6837, -2.3087],
[-1.5623, -0.2522]])
tensor([[ 4.0597],
[ 2.2267],
[10.5830],
[-0.1603],
[ 7.5412],
[ 4.3141],
[ 4.9181],
[ 4.2847],
[ 8.6720],
[ 1.9464]])
在读取完数据后我们就可以进入训练阶段(以后为训练前所需要做的步骤)
1.初始化权重w,因为w是需要参与计算的梯度的
2.初始化偏差标量b
3.定义模型linreg
4.定义损失函数
4.定义梯度优化函数
###定义初始化模型参数 w 与b
w = torch.normal (0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(size=(1,1), requires_grad=True) ## 因为偏差是个标量 所以size为1*1
def linreg(X, w, b):
'''线性回归模型'''
return torch.matmul(X, w) + b
def squared_loss(y_hat, y):
''''均方损失'''
return (y_hat-y.reshape(y_hat.shape))**2 / 2 ###向量大小可能不一样,所以统一reshape 成size(y_hat)
def sgd(params, lr, batch_size): ##
'''
1. params :给定所有参数
2. lr:学习率
3. batch_size: 输入的批次量大小
小批量随机梯度下降
'''
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_() ##torch不会自动将梯度重新设置为0,这里需手动设置
接下来我们就可以进入训练阶段了(设置好lr(学习率),epoch(迭代次数))
lr = 0.03
num_epochs = 20
net = linreg
loss = squared_loss
for epoch in range (num_epochs):
for X,y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y)
l.sum().backward()
sgd([w,b], lr, batch_size)
with torch.no_grad():
train_1 = loss(net(features, w, b), labels)
print(f'epoch{epoch + 1}, loss{float(train_1.mean()):f}')
## 人工数据集 可以手动查看误差
print(f'w的估计误差:{true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差:{true_b - b}') ## b 是个标量 不需要resize
简易版实现
import torch
from torch.utils import data
from torch import nn
'''
1.构造数据集(需要定义好特征向量和标签向量)
2.构造迭代器 每次训练随机从样本里面选取
3.定义网络函数
4.训练 计算误差
'''
def synthetic_data(w, b, num_examples):
X = torch.normal(0, 0.01,(num_examples, len(w)))
y = torch.matmul(X, w) +b
y += torch.normal(0, 0.01, y.shape)
return X, y.reshape(-1,1)
true_w = torch.tensor([2,-3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 100)
def load_array(data_arrays, batch_size, is_Train=True):
'''构造一个PyTorch数据迭代器'''
dataset = data.TensorDataset(*data_arrays) ## 生成一个datasets的向量
return data.DataLoader(dataset, batch_size, shuffle=is_Train)
batch_size = 10
data_iter = load_array((features,labels), batch_size) ## 用TensorDataset读取 features 和lables 输入
next(iter(data_iter))
## 定义模型
net = nn.Sequential(nn.Linear(2,1))
# net[0].weight.data.normal_(0,0.01) # 重新设置网络层的数据
# net[0].bias.data.fill_(0)
loss = nn.MSELoss() ## 均方误差
trainer = torch.optim.SGD(net.parameters(), 0.03)
num_epochs = 20
for epoch in range (num_epochs):
for X,y in data_iter:
l = loss(net(X),y)
trainer.zero_grad() ## 优化器梯度清零
l.backward() #torch已经帮我们实现了sum
trainer.step()
l = loss(net(features), labels)
print(f'epoch {epoch + 1}, loss {l:f}')
麻雀虽小五脏俱全,希望在今后的学习里能对以下步骤有更深的理解而不仅仅是停留在表面
编写数据------>读取数据------->定义模型-------->设置损失函数------->定义训练模型参数------->打印结果