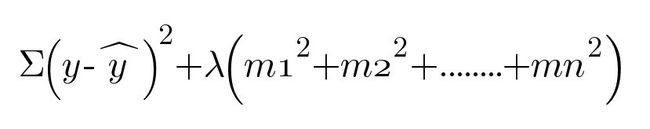l1正则化和l2正则化
I have read many articles on the topic to find out which is better out of two and what should I use for my model. I wasn’t satisfied with any of them and that left my brain confused which one should I use? After having done so many experiments, I have finally found out all answers to Which Regularization technique to use and when? Let’s get to it using a regression example.
我已经阅读了很多关于该主题的文章,以找出其中最好的两个,以及我应该在模型中使用什么。 我对它们中的任何一个都不满意,这让我的大脑感到困惑,我应该使用哪个? 经过大量的实验之后,我终于找到了使用哪种正则化技术以及何时使用的所有答案。 让我们使用一个回归示例。
Let’s suppose we have a regression model for predicting y-axis values based on the x-axis value.
假设我们有一个基于x轴值预测y轴值的回归模型。
Cost Function 成本函数While training the model, we always try to find the cost function. Here, y is the actual output variable and ŷ is the predicted output. So, for the training data, our cost function will almost be zero as our prediction line passes perfectly from the data points.
在训练模型时,我们总是尝试找到成本函数。 此处,y是实际输出变量,而ŷ是预测输出。 因此,对于训练数据,当我们的预测线完美地从数据点经过时,我们的成本函数将几乎为零。
Now, suppose our test dataset looks like as follows
现在,假设我们的测试数据集如下所示
Model on the test dataset 在测试数据集上建模Here, clearly our prediction is somewhere else and the prediction line is directed elsewhere. This leads to overfitting. Overfitting says that with respect to training dataset you are getting a low error, but with respect to test dataset, you are getting high error.
在这里,显然我们的预测在其他地方,而预测线则在其他地方。 这导致过度拟合。 过拟合表示,相对于训练数据集,您得到的误差很小,但是相对于测试数据集,则得到的误差很高。
Remember, when we need to create any model let it be regression, classification etc. It should be generalized.
记住,当我们需要创建任何模型时,让它为回归,分类等。应该对其进行概括。
We can use L1 and L2 regularization to make this overfit condition which is basically high variance to low variance. A generalized model should always have low bias and low variance.
我们可以使用L1和L2正则化来制作这种过拟合条件,该条件基本上是高方差到低方差。 广义模型应始终具有低偏差和低方差。
Let’s try to understand now how L1 and L2 regularization help reduce this condition.
现在让我们尝试了解L1和L2正则化如何帮助减少这种情况。
We know the equation of a line is y=mx+c.
我们知道一条线的方程是y = mx + c。
For multiple variables this line will transform to y = m1x1 + m2x2 + …….. + mn xn.
对于多个变量,此行将转换为y = m1x1 + m2x2 +…….. + mn xn。
Where m1, m2, …., mn are slopes for respective variables, and x1, x2, ...., xn are the variables.
其中,m1,m2,……,mn是各个变量的斜率,x1,x2,……,xn是变量。
When the coefficients (i.e. slopes) of variables are large any model will go to overfitting condition. why does this happen? The reason is very simple, the higher the coefficient the higher the weight of that particular variable in the prediction model. And we know not every variable have a significant contribution. Regularization works by penalizing large weights. Thus enabling highly correlated variables have high weights and less correlated variables having a lower weight.
当变量的系数(即斜率)较大时,任何模型都将过拟合。 为什么会这样? 原因非常简单,系数越高,预测模型中该特定变量的权重就越高。 而且我们知道并非每个变量都有重大贡献。 正则化通过惩罚较大的权重而起作用。 因此,使高度相关的变量具有较高的权重,而较少相关的变量具有较低的权重。
The regularization method is a hyperparameter as well, which means it can be tuned through cross-validation.
正则化方法也是一个超参数,这意味着可以通过交叉验证对其进行调整。
L1正则化或套索回归 (L1 Regularization or Lasso Regression)
A regression model that uses the L1 regularization technique is called Lasso Regression
使用L1正则化技术的回归模型称为套索回归
The L1 regularization works by using the error function as follows —
L1正则化通过使用以下误差函数来工作:
For tuning our model we always want to reduce this error function. λ parameter will tell us how much we want to penalize the coefficients.
为了调整我们的模型,我们总是想减少这个误差函数。 λ参数将告诉我们要罚多少系数。
0 < λ< ∞ (0 < λ < ∞)
If λ is large, we penalize a lot. If λ is small, we penalize less. λ is selected using cross-validation.
如果λ大,我们将受到很多惩罚。 如果λ小,我们将减少惩罚。 使用交叉验证选择λ 。
How our model is tuned by this error function?
这个误差函数如何调整我们的模型?
Earlier our error function (or cost function ∑ (y -ŷ )²) was solely based on our prediction variable ŷ. But now we have λ(|m1|+|m2|+ . . . . + |mn|) as an additional term.
先前我们的误差函数(或成本函数∑(y-ŷ)² )仅基于我们的预测变量prediction。 但是现在我们有了λ(| m1 | + | m2 | + .... + + mn |)作为附加项。
Earlier the cost function ∑ (y -ŷ )²) = 0 since our line was passing perfectly through training data points.
由于我们的直线完美地通过了训练数据点,因此成本函数∑(y-ŷ)² ) = 0较早。
let λ = 1 and |m1|+|m2|+ . . . . + |mn| = 2.8
令λ= 1且| m1 | + | m2 | +。 。 。 。 + | mn | = 2.8
Error function = ∑ (y -ŷ )²) + λ(|m1|+|m2|+ . . . . + |mn|) = 0 + 1*2.8 = 2.8
误差函数= ∑(y-ŷ)² ) + λ(| m1 | + | m2 | +。。。+ | mn |)= 0 + 1 * 2.8 = 2.8
While tuning, our model will now try to reduce this error of 2.8. lets say now value of ∑ (y -ŷ )²) = 0.6, λ = 1 and |m1|+|m2|+ . . . . + |mn| = 1.1
在调整时,我们的模型现在将尝试减少2.8的误差。 假设现在的值∑(y-ŷ)² )= 0.6,λ= 1并且| m1 | + | m2 | +。 。 。 。 + | mn | = 1.1
Now, the new value of Error function will be
现在,错误函数的新值将是
Error function = ∑ (y -ŷ )²) + λ(|m1|+|m2|+ . . . . + |mn|) = 0.6 + 1*1.1 = 1.7
误差函数= ∑(y-ŷ)² ) + λ(| m1 | + | m2 | +。。。+ | mn |)= 0.6 + 1 * 1.1 = 1.7
This will iterate multiple times. For reducing the error function our slopes will decrease simultaneously. Here we will see the slopes will get less and less steep.
这将重复多次。 为了减小误差函数,我们的斜率将同时减小。 在这里,我们将看到坡度越来越小。
As the λ value will get higher, it’ll penalize the coefficients more and the slope of the line will go more towards zero.
随着λ值变高,它将对系数造成更多的惩罚,并且直线的斜率将更趋于零。
In case of L1 regularization due to taking |slope| in the formula, the smaller weights will eventually die out and become 0. That means L1 regularization help select features which are important and turn the rest into zeros. It’ll create sparse vectors of weights as a result like (0, 1, 1, 0, 1). So, this works well for feature selection in case we have a huge number of features.
如果由于| slope |而导致L1正则化在公式中,较小的权重最终将消失并变为0。这意味着L1正则化有助于选择重要的特征,并将其余特征变为零。 结果将创建权重的稀疏向量,例如(0,1,1,0,1)。 因此,在我们拥有大量功能的情况下,这对于选择功能非常有效。
L2正则化或岭回归 (L2 Regularization or Ridge Regression)
A regression model that uses L2 regularization technique is called Ridge Regression.
使用L2正则化技术的回归模型称为Ridge回归。
The L2 regularization works by using the following error function
L2正则化通过使用以下误差函数来工作
Error function for L2 regularization L2正则化的误差函数L2 regularization works similar to the way how L1 works as explained above. The only difference comes into play with the slopes. In L1 regularization we were taking |slope| while here we are taking slope².
L2正则化的工作方式与上述L1的工作方式相似。 唯一的区别在于坡度。 在L1正则化中,我们采用| slope |。 而在这里,我们采取坡度² 。
This will work similarly it’ll penalize the coefficients and the slope of the line will go more towards zero, but will never equal zero.
这将类似地起作用,它将惩罚系数,并且直线的斜率将更趋向于零,但永远不会等于零。
Why is it so?
为什么会这样呢?
This is because of us using slope² in the formula. This method will create sparsity of weights in the form of (0.5, 0.3, -0.2, 0.4, 0.1). Let’s understand this sparsity by an example.
这是因为我们在公式中使用了斜率²。 此方法将创建( 0.5,0.3,-0.2,0.4,0.1)形式的权重稀疏性。 让我们通过一个例子来理解这种稀疏性。
consider the weights (0 , 1) and (0.5, 0.5)
考虑权重(0,1)和(0.5,0.5)
For the weights (0, 1) L2 : 0² + 1² = 1
对于砝码(0,1)L2:0²+1²= 1
For the weights (0.5, 0.5) L2 : 0.5² + 0.5² = 0.5
对于砝码(0.5,0.5)L2:0.5²+0.5²= 0.5
Thus, L2 regularization will prefer the vector point (0.5, 0.5) over the vector (1, 1) since this produces a smaller sum of squares and in turn a smaller error function.
因此,L2正则化将优先选择矢量点(0.5、0.5),而不是矢量(1、1),因为这会产生较小的平方和,进而产生较小的误差函数。
Let’s connect on LinkedIn. You may also reach out to me via [email protected].
让我们在LinkedIn上连接。 您也可以通过[email protected]与我联系。
翻译自: https://levelup.gitconnected.com/l1-vs-l2-regularization-and-when-to-use-which-cd3382008774
l1正则化和l2正则化