PR曲线以及ROC曲线的简单理解

首先，了解一下混淆矩阵，如下表：

 

其中TP+FP+TN+FN = 样例总数 

查准率P：P=TP/(TP+FP)

查全率R：R=TP/(TP+FN)

TP：把正例正确的分类为正例

FN：把正例错误的分类为反例

TN：把反例错误的分类为正例

FP：把反例正确的分类为反例

真正率TPR：预测为正例且实际为正例的样本占所有正例样本（真实结果为正例样本）的比例

TPR = TP/(TP+PN)

假正率FPR：预测为正例但实际为负例的样本占所有负例样本（真是结果为负例样本）的比例

FPR = FP/(FP+TN)

举个例子

编号	Label	预测指标	预测结果	是否正确
1	真	0.99	正例	是
2	真	0.96	正例	是
3	真	0.94	正例	是
4	真	0.88	正例	是
5	假	0.73	正例	否
6	真	0.70	反例	否
7	假	0.65	反例	是
8	假	0.55	反例	是
9	假	0.13	反例	是
10	假	0.01	反例	是

此时的混淆矩阵为

真实情况	预测结果
	正例	反例
正例	4	1
反例	1	4

此时查准率P和查全率R为

P=TP/(TP+FP)=4/(4+1)=0.8

R=TP/(TP+FN)=4/(4+1)=0.8

PR曲线

PR曲线中的P代表的是查准率（precision），R代表的是查全率（recall），PR图直观地显示出学习器在样本总体上的查全率、查准率。

在很多情形下，我们可根据学习器的预测结果对样例进行排序，排在前面的是学习器认为“最可能”是正例的样本。按此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、查准率。以查准率为纵轴、查全率为横轴作图，就得到了查准率—查全率曲线，简称“P- R曲线”，显示该曲线的图称为“P—R图”

​​​​​​​​​​​​​​ 

在众多学习器的P- R曲线被另一个学习器的曲线完全“保住”，则可断言后者的性能优于前者，例如图2.3中学习器A的性能优于学习器C；但是A和B发生交叉，那性能应该如何判断？

引入一个综合考虑查准率和查全率的性能度量：平衡点（BEP），它是“查准率=查全率是的取值（斜率为1），例如学习器C的BEP是0.64，而基于PEB的比较可认为学习器A优于B。

但BEP还是过于简化了些，更常用的是F1度量：

F1=2*P*R/(P+R)=2*TP/(样例总数+TP-TN）

PC曲线的绘制

参考博客http://t.csdn.cn/azin2

需要导入第三方库matplotlib、numpy及sklearn。

#coding:utf-8
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
from sklearn.utils.fixes import signature
plt.figure("P-R Curve")
plt.title('Precision/Recall Curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
#y_true为样本实际的类别，y_scores为样本为正例的概率
y_true = np.array([1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0])
y_scores = np.array([0.9, 0.75, 0.86, 0.47, 0.55, 0.56, 0.74, 0.62, 0.5, 0.86, 0.8, 0.47, 0.44, 0.67, 0.43, 0.4, 0.52, 0.4, 0.35, 0.1])
precision, recall, thresholds = precision_recall_curve(y_true, y_scores)
#print(precision)
#print(recall)
#print(thresholds)
plt.plot(recall,precision)
plt.show()

ROC曲线

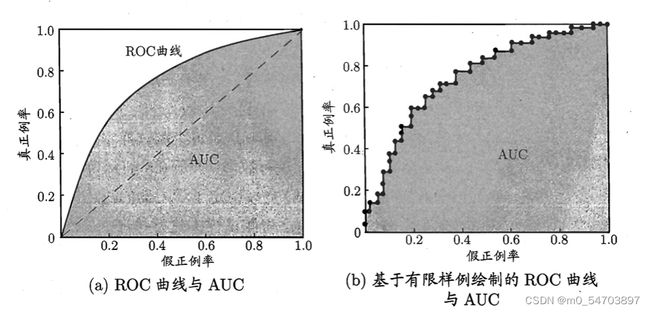
与P- R曲线相似，我们根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值以“真正例率”为纵轴，“假正例率”为横轴作图，就得到ROC曲线。

进行机器学习的比较时，与P- R图相似，若一个机器学习的ROC曲线被另一个机器学习的曲线完全“包住”，则可以断言后者的性能优于前者；若两个学习器的ROC曲线发生交叉，则难以一般性地断言两者孰优孰劣。AUC是ROC曲线下的面积，介于0.1和1之间，作为数值能够直观的评价分类器的好坏，值越大越好。