python scatter参数详解_python数据可视化seaborn（二）—— 分布数据可视化

这篇文章是Python可视化seaborn系列的第二篇文章，本文将详解seaborn如何探索数据的分布。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
% matplotlib inline

sns.set(context='notebook',font='simhei',style='whitegrid')
# 设置风格尺度和显示中文

import warnings
warnings.filterwarnings('ignore')  # 不发出警告

单变量

直方图 displot

seaborn.distplot(a, bins=None, hist=True, kde=True, rug=False, fit=None, hist_kws=None, kde_kws=None, rug_kws=None, fit_kws=None, color=None, vertical=False, norm_hist=False, axlabel=None, label=None, ax=None)

• bins → 箱数
• hist、ked、rug → bool,是否显示箱/密度曲线/数据分布
• norm_hist → 直方图是否按照密度来显示，如果为False,显示计数
• {hist，kde，rug，fit} _kws：字典，对应部分的各种参数。
• vertical → 是否水平显示
• fit → 可结合scipy库在图像上做拟合
• label → 图例
• axlabel → x轴标注

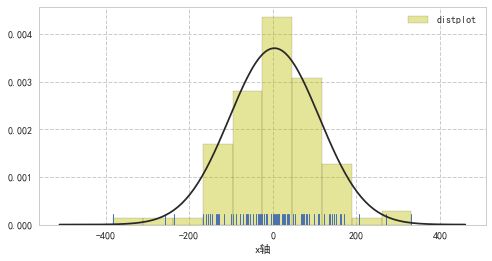
# 直方图
from scipy.stats import norm #使用直方图和最大似然高斯分布拟合绘制分布

rs = np.random.RandomState(50)  # 设置随机数种子
s = pd.Series(rs.randn(100)*100)

plt.figure(figsize=(8,4))
sns.distplot(s, bins=10, hist=True, kde=False, norm_hist=False,
            rug=True, vertical=False,label='distplot',
            axlabel='x轴',hist_kws={'color':'y','edgecolor':'k'},
            fit=norm)
# 用标准正态分布拟合
plt.legend()
plt.grid(linestyle='--')
plt.show()

plt.figure(figsize=(8,4))
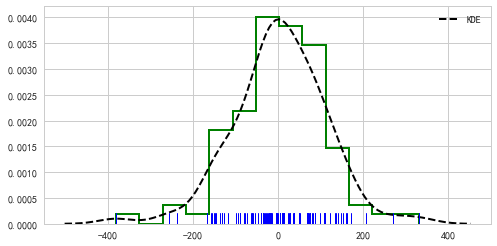
sns.distplot(s,rug = True,
            rug_kws = {'color':'b'} ,
            # 设置数据频率分布颜色
            kde_kws={"color": "k", "lw": 2, "label": "KDE",'linestyle':'--'},
            # 设置密度曲线颜色，线宽，标注、线形
            hist_kws={"histtype": "step", "linewidth": 2,"alpha": 1, "color": "g"})  
            # 设置箱子的风格、线宽、透明度、颜色
            # 风格包括：'bar', 'barstacked', 'step', 'stepfilled'
plt.show()

核密度估计图 kdeplot

核密度估计的步骤：

• 每一个观测附近用一个正态分布曲线近似
• 叠加所有观测的正态分布曲线
• 归一化

seaborn.kdeplot（data，data2 = None，shade = False，vertical = False，kernel ='gau'，bw ='scott'，gridsize = 100，cut = 3，clip = None，legend = True，cumulative = False，shade_lowest = True，cbar = False，cbar_ax =无，cbar_kws =无，ax =无， kwargs ）

• shade: 如果为True，则用颜色填充KDE曲线下方的区域（或者在数据为双变量时用颜色填充的轮廓）
• kernel: {‘gau’|‘cos’|‘biw’|‘epa’|‘tri’|‘triw’} 用于拟合的核，双变量值能用高斯核（gau）
• bw: {'scott'|'silverman'|标量|一对标量} 确定核的大小，近似理解为拟合程度，bw越大，曲线越平缓。
• gridsize：int, 网格中的离散点数
• cumulative ：是否绘制累积分布
• cbar：参数若为True，则会添加一个颜色条(颜色条在双变量kde图像中才有)

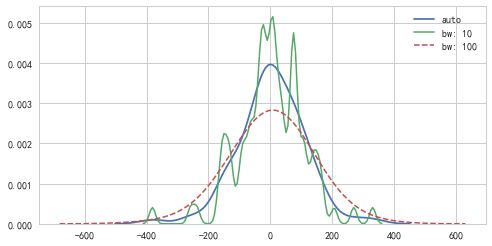
# 单个样本数据密度分布图
plt.figure(figsize=(8,4))

sns.kdeplot(s,label='auto')
sns.kdeplot(s,bw=10, label="bw: 10",linewidth = 1.5)
sns.kdeplot(s,bw=100, label="bw: 100",linestyle = '--',linewidth = 1.5)
# bw → 也可以类似看做直方图的箱数，数越大，箱子越多，刻画的越精确。
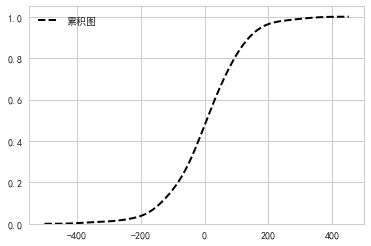
plt.show()

sns.kdeplot(s, label="累积图",color='k',cumulative=True,
            linestyle = '--',linewidth = 2)
plt.show()

核密度分布图不但能绘制单个变量的，也能绘制双变量！！！

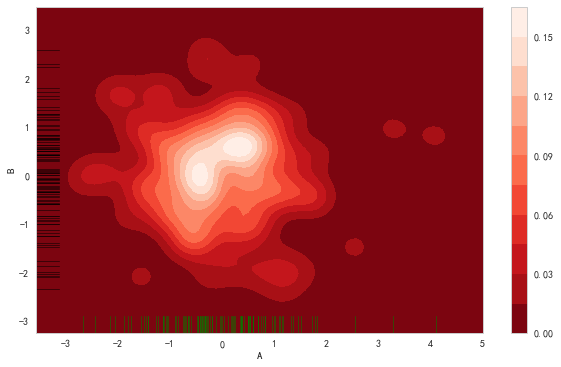
# 2、密度图 - kdeplot()
# 两个样本数据密度分布图

rs = np.random.RandomState(2)  # 设定随机数种子
df = pd.DataFrame(rs.randn(100,2),
                 columns = ['A','B'])

fig = plt.figure(figsize=(10,6))
sns.kdeplot(df['A'],df['B'],
           cbar = True,    # 是否显示颜色图例
           shade = True,   # 是否填充
           cmap = 'Reds_r',  # 设置调色盘
           shade_lowest=True,  # 最外围颜色是否显示
           n_levels = 10,   # 曲线个数（越大，越密集）
           bw = .3
           )
# 两个维度数据生成曲线密度图，以颜色作为密度衰减显示

sns.rugplot(df['A'], color="g", axis='x',alpha = 0.5)
sns.rugplot(df['B'], color="k", axis='y',alpha = 0.5)
# 注意设置x，y轴

双变量

jointplot

seaborn.jointplot（x，y，data = None，kind ='scatter'，color = None，height= 6，ratio = 5，space = 0.2，dropna = True，xlim = None，ylim = None，joint_kws = None，marginal_kws =None，annot_kws =None， kwargs ）

该函数是JoinGrid类的一个轻量级界面，如果想更加灵活的绘制，可以使用JoinGrid函数

• kind: 设置类型：“scatter”、“reg”、“resid”、“kde”、“hex”
• height: int, 图像大小（图像自动调整为正方形）
• radio: int, 主图与边缘图的高度比
• space: # 设置主图和边缘图的间距
• {x，y} lim ：在绘图之前设置轴限制
• {joint，marginal，annot} _kws：dicts 绘图组件的其他关键字参数

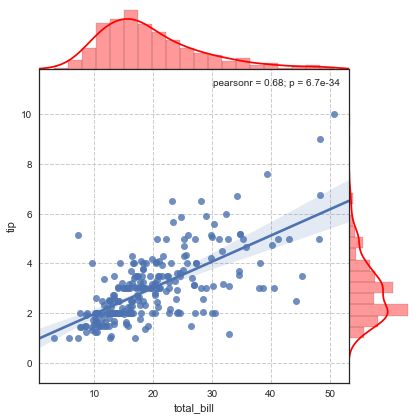
# 散点图 + 边缘直方图

tips = sns.load_dataset("tips")

sns.jointplot(x='total_bill', y='tip',  # 设置xy轴，显示columns名称
              data=tips,   # 设置数据
              color = 'k',   # 设置颜色
              s = 50, edgecolor="w",linewidth=1,
              # 设置散点大小、边缘线颜色及宽度(只针对scatter）
              kind = 'scatter',
              space = 0.2,  # 设置散点图和布局图的间距
              height= 7, ratio = 5,  # 散点图与布局图高度比，整型
              marginal_kws=dict(bins=20, rug=True)  # 设置柱状图箱数，是否设置rug
              )
plt.show()

seaborn会直接给出变量的皮尔逊相关系数和P值
pearson相关系数计算：

https://zh.wikipedia.org/w/index.php?title=%E7%9A%AE%E5%B0%94%E9%80%8A%E7%A7%AF%E7%9F%A9%E7%9B%B8%E5%85%B3%E7%B3%BB%E6%95%B0&oldid=51962622​zh.wikipedia.org

• p：样本间的差异由抽样误差所致的概率小于p.

p-value - Wikipedia​en.wikipedia.org

# 回归图 + 边缘直方图

with sns.axes_style("ticks"):
    sns.jointplot(x='total_bill', y='tip',data = tips,
                  kind="hex", color="r",   # 主图为六角箱图
                  height=6,space=0.1,
                  joint_kws=dict(gridsize=20,edgecolor='w'),  # 主图参数设置
                  marginal_kws=dict(bins=20,color='g',
                                    hist_kws={'edgecolor':'k'}),   # 边缘图设置
                  annot_kws=dict(stat='r',fontsize=15))  # 修改统计注释

# 密度图

rs = np.random.RandomState(15)
df = pd.DataFrame(rs.randn(300,2),columns = ['A','B'])
# 创建数据
with sns.axes_style("white"):# 设置当前图的样式
    g = sns.jointplot(x=df['A'], y=df['B'],data = df,
                  kind="kde", color="k",shade_lowest=False)
# 创建密度图

    g.plot_joint(plt.scatter,c="r", s=30, linewidth=1, marker="+")
# 添加散点图

JointGrid

前面讲过jointplot其实是JoinGrid的一个封装，要想有更灵活的设置，可以使用JoinGrid类

• __init__（x，y，data = None，height= 6，ratio = 5，space = 0.2，dropna = True，xlim = None，ylim = None）
  方法：
• plot（joint_func，marginal_func ,annot_func)→ 绘制完整的图形
• plot_joint（func，** kwargs）→ 绘制双变量图形
• plot_marginals（func，** kwargs）→ 绘制边缘单变量图形
• savefig（ args，* kwargs）→ 保存
• set_axis_labels（[xlabel，ylabel]）→ 在双变量轴上设置轴标签。

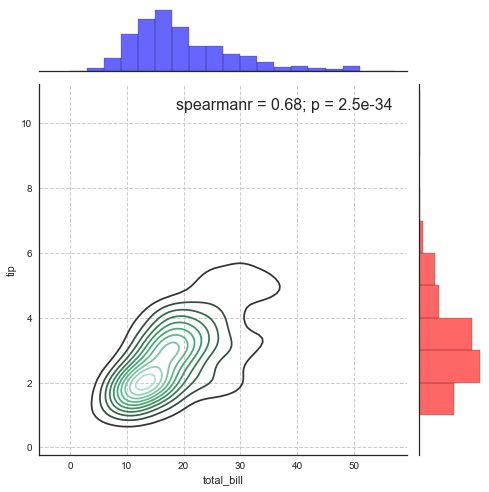
# 可拆分绘制的散点图
# plot_joint() + ax_marg_x.hist() + ax_marg_y.hist()

sns.set_style("white")
# 设置风格

g = sns.JointGrid(x="total_bill", y="tip", data=tips, height=7)
# 创建一个绘图表格区域，设置好x、y对应数据

g.plot_joint(sns.kdeplot, color ='m', edgecolor = 'white')  # 设置框内图表，scatter
g.ax_marg_x.hist(tips["total_bill"], color="b", alpha=.6,
                 edgecolor='k',bins=np.arange(0, 60, 3))
# 设置x轴直方图，注意bins是数组
g.ax_marg_y.hist(tips["tip"], color="r", alpha=.6,
                 orientation="horizontal",edgecolor='k',
                 bins=np.arange(0, 12, 1))
# 设置y轴直方图，注意需要orientation参数

from scipy import stats
g.annotate(stats.spearmanr , fontsize=16, loc='best')

# 设置标注，可以为pearsonr，spearmanr，或者是自定义的函数

plt.grid(linestyle = '--')

# 可拆分绘制的散点图
# plot_joint() + plot_marginals()

g = sns.JointGrid(x="total_bill", y="tip", data=tips,height=6.5,ratio=6)
# 创建一个绘图表格区域，设置好x、y对应数据

g = g.plot_joint(plt.scatter,color="g", s=50, edgecolor="white")   # 绘制散点图
plt.grid(linestyle = '--')  # 设置网格线
g.plot_marginals(sns.distplot, kde=True, hist_kws={'color':'g','edgecolor':'k'})  # 设置边缘图

rsquare = lambda a, b: stats.pearsonr(a, b)[0] ** 2   # 自定义统计函数
g = g.annotate(rsquare, template="{stat}: {val:.2f}",
               stat="$R^2$", loc="upper left", fontsize=16)  # 设置注释

# 1、综合散点图 - JointGrid()
# 可拆分绘制的散点图
# plot_joint() + plot_marginals()
# kde - 密度图

g = sns.JointGrid(x="total_bill", y="tip", data=tips,space=0)
# 创建一个绘图表格区域，设置好x、y对应数据

g = g.plot_joint(sns.regplot)     # 绘制密度图
plt.grid(linestyle = '--')
g.plot_marginals(sns.distplot, color="r",bins=20,hist_kws={'edgecolor':'k'})  # 绘制x，y轴密度图
g.annotate(stats.pearsonr)

探索两两变量之间的关系

通常我们的数据并不是只有一个或者两个变量，那么对于多个变量，我们常需要探索两两变量之间的分布及关系这是我们就需要使用pairplot函数 或者是PairGrid类

pairplot

seaborn.pairplot（data，hue = None，hue_order = None，palette = None，vars = None，x_vars = None，y_vars = None，kind ='scatter'，diag_kind ='auto'，markers = None，s = 2.5，aspect = 1，dropna = True，plot_kws = None，diag_kws = None，grid_kws = None）

• hue: string(变量名) ： 颜色将按照指定的变量分类
• hue_order ： list 设置调色板色调变量级别
• palette ： 调色板
• vars : list 变量名称列表，否则使用所有数值型变量的列
• markers: 点样式

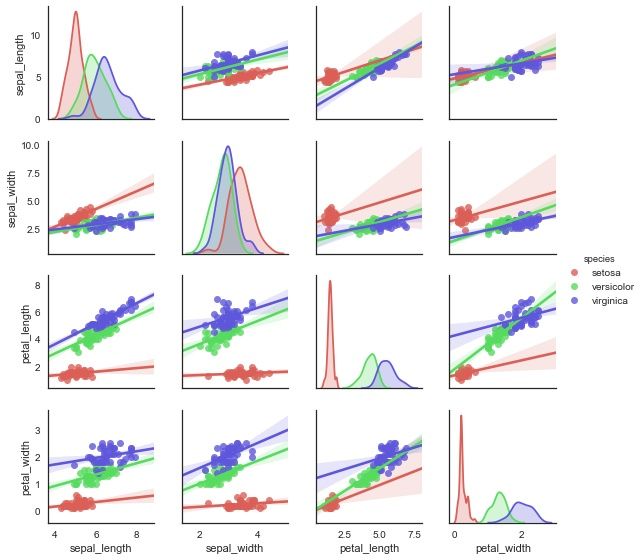
# 2、矩阵散点图 - pairplot()

# sns.set_style("white")
# 设置风格

iris = sns.load_dataset("iris")
print(iris.head())
# 读取鸢尾花数据

sns.pairplot(iris,
            kind = 'scatter',  # 散点图/回归分布图 {‘scatter’, ‘reg’}  
            diag_kind="hist",  # 设置对角线图直方图/密度图 {‘hist’, ‘kde’}
            hue="species",   # 按照某一字段进行分类
            palette="husl",  # 设置调色板
            markers=["o", "s", "D"],  # 设置不同系列的点样式（这里根据参考分类个数）
            height= 2,   # 图表大小
            plot_kws={'s':20},    # 设置点大小
            diag_kws={'edgecolor':'w'})  # 设置对角线直方图样式
plt.show()

sepal_length sepal_width petal_length petal_width species
5.1 3.5 1.4 0.2 setosa
4.9 3.0 1.4 0.2 setosa
4.7 3.2 1.3 0.2 setosa
4.6 3.1 1.5 0.2 setosa
5.0 3.6 1.4 0.2 setosa

# 2、矩阵散点图 - pairplot()
# 其他参数设置

sns.pairplot(iris, kind="reg",hue='species', # 设置回归图形
             diag_kind='kde',palette='hls',  # 设置对角线图类型及调色盘
             diag_kws=dict(shade=True),height=2)

PairGrid

相当于jointplot 和 JointGrid的关系，PairGrid 对矩阵散点图有着更为灵活的控制

• __init__（data，hue = None，hue_order = None，palette = None，hue_kws = None，vars = None，x_vars = None，y_vars = None，diag_sharey = True，height= 2.5，aspect = 1，despine = True，dropna = True）
  方法：
• add_legend（[legend_data，title，label_order]）绘制一个图例，可能将其放在轴外并调整图形大小。
• map_diag（func，** kwargs）：在每个对角线子图上绘制具有单变量函数的图。
• map_lower（func，** kwargs）：在下对角线子图上绘制具有双变量函数的图。
• map_upper（func，** kwargs）：在上对角线子图上绘制具有双变量函数的图
• map_offdiag（func，** kwargs）：在非对角线子图上绘制具有双变量函数的图。
• set（** kwargs）：在每个子图集Axes上设置属性。

# 2、矩阵散点图 - PairGrid()
# 可拆分绘制的散点图
# map_diag() + map_offdiag()

g = sns.PairGrid(iris,hue="species",palette = 'hls',height=2,
                vars = ['sepal_length','sepal_width','petal_length','petal_width'],  # 可筛选
                )
# 创建一个绘图表格区域，设置好x、y对应数据，按照species分类

g.map_diag(plt.hist,
           histtype = 'barstacked',   # 可选：'bar', 'barstacked', 'step', 'stepfilled'
           linewidth = 1, edgecolor = 'w')
# 对角线图表，plt.hist/sns.kdeplot

g.map_offdiag(plt.scatter,
              edgecolor="w", s=40,linewidth = 1   # 设置点颜色、大小、描边宽度
                )
# 其他图表，plt.scatter/plt.bar...

g.add_legend()
# 添加图例
# 2、矩阵散点图 - PairGrid()
# 可拆分绘制的散点图
# map_diag() + map_lower() + map_upper()

g = sns.PairGrid(iris[iris['species']=='versicolor'])
g.map_diag(sns.kdeplot, lw=3)   # 设置对角线图表
g.map_upper(sns.regplot, color = 'b')     # 设置对角线上端图表
g.map_lower(sns.kdeplot, cmap="Blues_d")      # 设置对角线下端图表

看再多次，都不如自己亲自动手写一次，只有在实际应用中不断练习，思考，调整。才能理解掌握数据可视化的技能。

下篇文章，我会介绍seaborn如何探索数据间的关系。