共指消解评测方法详解与python实现

0. 简介

在共指消解任务中，如何去评价一个结果的好坏，是一件非常值得讨论的事情，不管是实体共指还是事件共指，都绕不开这个话题。例如现在有这样一个场景，正确的实体共指结果应该是$a_1,a_2,a_3$为一个实体$b_1,b_2,b_3$为另一个实体，共指系统1将结果预测成了$a_1,a_2$，$b_1,b_2$，以及$a_3,b_3$这三个实体，而共指系统2将结果预测成了$a_1,a_2,a_3$，$b_1$，$b_2$，以及$b_3$这四个实体，很明显，这两个共指结果都是错的，可是怎样量化的去评价系统1和系统2谁的结果更好呢？这就是共指消解评测指标所研究的内容。

然而，限于篇幅，近些年发表的论文中，一般很少有具体的描述评测指标到底是怎样计算，而只是贴出模型最终在各个指标下的评测结果，而网上相关的可以参考的解释也非常少，或者介绍的不够清晰明白。由于历史原因，相关的代码中评测的部分一般都是使用某个会议或者数据集发布的官方评测工具，一般是由perl编写的，对于我来说可读性太差。几番辗转之后终于找到一篇总结的很好的论文，参考这篇论文的例子，本文将详细介绍包括MUC、B³、CEAF、BLANC等指标。

1. 基本概念

在开始介绍各项指标之前，先介绍一下基本概念。

• mention： （不知道怎么翻译）。某个实体（或事件）在原文中的一次出现，可以是它的名字，也可以是指代，例如“某地发生了7.0级地震，这次地震造成超过了30人伤亡。”其中加粗的部分就是“地震”这个事件的两个mention。
• key：真实的共指簇，如果只考虑共指，不考虑链接的话，每个簇就是一个实体。每个簇由若干个mention构成。
• response：系统预测输出的共指簇。

在引入了共指消解任务之后，一些概念可能跟只考虑NER任务时变得不一样。通常，在面临一个NER任务时，我们一般把原文中识别出来的片段直接称作实体，而实际上，这些span是属于某些实体的mention。而经过实体共指之后，这些mention会形成若干簇，在我看来，严格地讲，此时还不能将它们称作entity，而是称作cluster比较合适，因为如果没有经过实体链接任务，其实这个时候只是知道这些mention所指是同一个实体，而并没有明确这一实体是谁。

至于实体链接任务，其本质上可以看做是query的匹配，即文本中出现的实体，与数据库中的条目进行匹配。关于实体链接的研究，本文不做讨论，所以在下文中，也会不区分entity和cluster，混用这两个概念。

2. 具体介绍

2.1 MUC

MUC，Message Understanding Conference，是系列会议，关于MUC-1到MUC-6的评测简介，可以参考这篇https://dl.acm.org/doi/pdf/10.3115/1072399.1072401。

下面举例说明MUC指标的计算，例子来自于参考文献。

假设有两个实体，实体1有3个mention，分别记作$a,b,c$，实体2有4个mention，分别记作$d,e,f,g$，经过共指系统的预测，预测出了三组response，分别为$a,b$， $c,d$，以及$f,g,h,i$。其中mention $e$被漏掉了，没有被识别出来，mention $h$和mention $i$是被错误识别出来的：

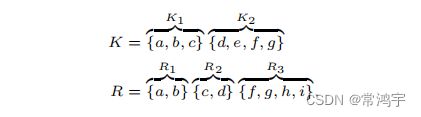
下图的最左边的图，实线圈起来的，是正确的标注结果Key，虚线圈起来的是系统输出的结果Response：

那么中间的图和右边的图是什么意思呢？这里就要引入“截断”的概念。

• 以Key去截断Response：
  在左边的图中，把实线想象成可以割断虚线的“刀子”，把虚线切开，就得到了中间的图。
• 以Response去截断Key：
  同样以左边的图为基础，但是把虚线想象成“刀子”，把实线切开，就得到了右边的图。

在MUC的定义下，精确率和召回率的计算分别如下：

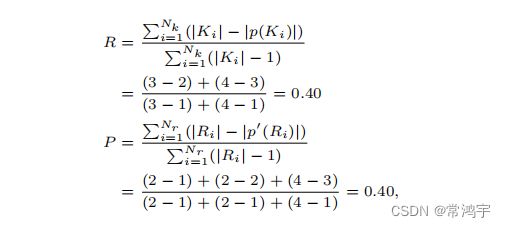
解释一下，$p(K_i)$是对于第i个实体，以Key去截断Response的结果，所以对于第一个实体，Key的结果中，有三个mention，以第一个实线去截断，在Response中得到了两个簇，分别是$a,b$和$c$（中间的图上边），所以是（3 - 2），同理对于第二个实体，计算就是（4 - 3）。如果Response的结果与Key完全相同，则截断之后每一个实线圈里，就只有一个虚线圈，对应分母上的减1，这是时候计算出来的Recall就是1.0；

类似的，$p^{\prime }(K_i)$就是对于第i个实体，以Response去截断Key的结果。

2.2. B3

B3的定义比较拗口，但直接看例子其实挺好理解的：

其中$\frac{2^2}{3}$的分子2，指的就是$a,b$；

同理$\frac{1^2}{3}$的分子1，指的是$c$，$\frac{1^2}{4}$的分子1，指的是$d$，以此类推。

2.3 CEAF

CEAF指标是由两个步骤组成的。

首先是对齐，即建立Response与Key之间的对应关系。在上面的例子中，$R_1$被对齐到$K_1$，$R_3$被对齐到$K_2$，$R_2$被舍弃了。至于为什么这样对齐，我所参考的概述文献里并没有介绍，根据结果推测，应该是按照匹配mention的数量进行判断的。

这里延伸出两个指标，分别是$CEA{F}_m$和$CEA{F}_e$。分别来介绍这两个指标：

$CEA{F}_m$的思想非常直接，计算每一对对齐之后的结果的公共部分mention的个数总和，除以所有Key的mention总和，就是召回率，除以Response的mention总和，就是精确率。

在它的基础上，还有一个稍微复杂一点的指标$CEA{F}_e$：

其中：

2.4 BLANC

注意，这里介绍的BLANC并不是原始的BLANC，而是参考文献1中作者改进版。

定义$C_k$, $C_r$分别是Key和Response的结果中，同一个圈圈中的元素两两组合的结果，$N_k$和$N_r$则是在不同的圈圈中组合出来的结果，那么根据定义，在上面的例子中分别有：

于是，基于C的指标和基于N的指标分别计算如下：


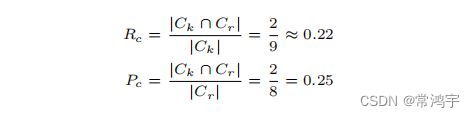
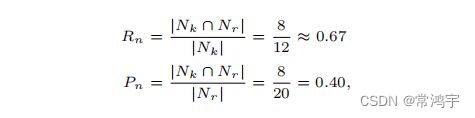
进而，可以根据这两组P和R计算出两个F，再对这两个F取平均就得到了最终的BLANC指标。

2.5 AVG

最后再提一下另一篇论文，参考文献2，其中提到了一个AVG指标，按照论文中的描述，就是对上述的各项指标取了平均。

这篇文献是对我帮助比较大的一篇文献，它主要提出了一个门控的机制，将事件mention的各种特征（是否真实发生、情感倾向等）与事件的表征进行了分解。这篇论文我也实验过，感觉在同一篇新闻里事件共指效果还可以，但是跨篇章的话很容易出错，并没有其给出的例子效果那么好，所以后来我采用了其他策略处理跨篇章共指。另外对于事件mention的额外特诊，事件是否真实发生这一特征比较有用，但是完全可以作为一个分类器直接判断，做特征分解好像有点太折腾了。

如果有同学想要以这篇文章为基础建立共指系统，我个人认为其事件共指部分可以采用，但是实体共指部分可以参考其他项目。

与之相关的一个项目是同一团队在21年还是20提出的一篇关于事件表征的论文，简称GENE，感兴趣的同学也可以读一下。

3. python实现

鉴于perl版本的评测指标使用起来不方便，我根据论文里的描述，结合自己的一点理解，写了各类指标的python版本，供大家参考。

首先写一个基类给下面各类使用：

from typing import Set, List


def flatten(l):
    """
    list的嵌套变成长list
    :param l: [[1, 2], [3, 4]]
    :return:  [1, 2, 3, 4]
    """
    return [item for sublist in l for item in sublist]


class BaseCorefMetric:
    def __init__(self, **args):
        pass

    def calculate_p(self, keys: List, responses: List) -> float:
        """
        计算精确率
        """
        raise NotImplementedError

    def calculate_r(self, keys: List, responses: List) -> float:
        """
        计算召回率
        """
        raise NotImplementedError

    def calculate_f(self, keys: List, responses: List) -> float:
        """
        计算F1
        """
        p = self.calculate_p(keys, responses)
        r = self.calculate_r(keys, responses)
        return (2 * p * r) / (p + r)

以及前文中用到的例子：

keys = [set(['a', 'b', 'c']), set(['d', 'e', 'f', 'g'])]
responses = [set(['a', 'b']), set(['c', 'd']), set(['f', 'g', 'h', 'i'])]

3.1 MUC

这个比较简单，直接按照定义实现即可。

class MUC(BaseCorefMetric):
    """
    计算MUC评价指标
    ---------------
    ver: 2022-10-25
    by: changhongyu
    """

    def calculate_p(self, keys: List[Set], responses: List[Set]) -> float:
        partitions = []
        for response in responses:
            partition = 0
            un = set()
            for key in keys:
                if response.intersection(key):
                    partition += 1
                    un = un.union(key)
            partition += len(response - un)
            partitions.append(partition)
        numerator = sum([len(response) - partition for response, partition in zip(responses, partitions)])
        denominator = sum([len(response) - 1 for response in responses])
        return numerator / denominator

    def calculate_r(self, keys: List[Set], responses: List[Set]) -> float:
        return self.calculate_p(responses, keys)

# muc = MUC()
# muc.calculate_f(keys, responses)   # 0.4

3.2 B3

这个也比较容易实现，按照定义写就好了。

class B3(BaseCorefMetric):
    """
    计算B3评价指标
    ---------------
    ver: 2022-10-25
    by: changhongyu
    """

    def calculate_p(self, keys: List, responses: List) -> float:
        numerator = sum([sum([(len(response.intersection(key)) ** 2 / len(response)) for key in keys])
                         for response in responses])
        denominator = sum([len(response) for response in responses])
        return numerator / denominator

    def calculate_r(self, keys: List, responses: List) -> float:
        return self.calculate_p(responses, keys)

3.3 CEAF

CEAF指标分为e和m两种，所以在计算的时候也做了区分。另外Key和Response的对齐是我按照自己的理解写的，对齐的基本原则如下：

1. response到key的匹配上的元素比率（匹配上的个数除以response的元素总数）越大的，越往前排；
2. 比率相同的，response和key元素总数越多的，越往前排；
3. 每个key只能与一个response匹配

class CEAF(BaseCorefMetric):
    """
    计算CEAF指标
    根据自己的理解写了Key和Response之间的匹配规则
    给定一个超参数ratio，当Response中的元素出现在Key中的比率大于ratio认为匹配上
    另外，匹配到某个Response的Key不能匹配给另一个Response
    ---------------
    ver: 2022-10-25
    by: changhongyu
    """

    def __init__(self, ratio: float = 0.5, kind: str = 'e'):
        """
        :param ratio: 超参数，判定Key和Response匹配上的阈值比率
        :param kind: 计算CEAFm指标还是CEAFe指标
        """
        super(CEAF, self).__init__()
        assert 0 < ratio <= 1, AssertionError('Input a ratio between 0 and 1.')
        assert kind in ['m', 'e'], AssertionError('Metric kind must be `e` or `m`.')
        self.ratio = ratio
        self.kind = kind
        self.pairs = None
        self.numerator = None

    def _align(self, keys: List, responses: List):
        """
        对齐Response和Key
        每个Key只能与一个Response对齐
        """
        # 所有符合条件的两两组合
        candidate_pairs = list(filter(lambda x: len(x[0].intersection(x[1])) / len(x[1]) >= self.ratio,
                                      sorted(flatten([[(key, response) for key in keys] for response in responses]),
                                             key=lambda x:
                                             len(x[0].intersection(x[1])) / len(x[1]) + (len(x[1]) + len(x[0])) * 1e-9,
                                             reverse=True)))
        # 按照匹配程度从高到低，为每一个pair中的Response选择对应的Key
        matched_pairs = []
        used_keys = []
        for pair in candidate_pairs:
            for response in responses:
                if response in pair and pair[0] not in used_keys:
                    matched_pairs.append(pair)
                    used_keys.append(pair[0])
                    break
        self.pairs = matched_pairs

    def _calculate_numerator(self):
        """
        为了避免在计算p和r的时候重复计算分子，所以把这个结果临时存储起来
        :return:
        """
        def f4(pair_):
            return 2 * (len(pair_[0].intersection(pair_[1]))) / (len(pair_[0]) + len(pair_[1]))

        assert self.pairs is not None
        if self.kind == 'm':
            self.numerator = sum([len(pair[0].intersection(pair[1])) for pair in self.pairs])
        else:
            self.numerator = sum([f4(pair) for pair in self.pairs])

    def _calculate_m(self, keys_or_responses: List) -> float:
        """
        计算CEAFm的精确率或召回率
        当传入Responses，计算的是精确率
        当传入Keys，计算的是召回率
        """
        if not self.numerator:
            self._calculate_numerator()
        return self.numerator / sum([len(k_or_r) for k_or_r in keys_or_responses])

    def _calculate_e(self, keys_or_responses: List) -> float:
        """
        计算CEAFe的精确率
        当传入Responses，计算的是精确率
        当传入Keys，计算的是召回率
        """
        if not self.numerator:
            self._calculate_numerator()
        return self.numerator / len(keys_or_responses)

    def calculate_p(self, keys: List, responses: List) -> float:
        if self.kind == 'm':
            return self._calculate_m(responses)
        elif self.kind == 'e':
            return self._calculate_e(responses)
        else:
            raise ValueError(self.kind)

    def calculate_r(self, keys: List, responses: List) -> float:
        return self.calculate_p(responses, keys)

    def calculate_f(self, keys: List, responses: List) -> float:
        """
        计算完f值后，要把pairs置为None，以便下次计算
        """
        if self.pairs is None:
            self._align(keys, responses)
        res = super(CEAF, self).calculate_f(keys, responses)
        self.pairs = None
        self.numerator = None
        return res

3.4 BLANC

BLANC指标有两项f值，最终输出的f值是这两项的平均。

class BLANC:
    """
    计算BLANC评测指标
    ---------------
    ver: 2022-10-26
    by: changhongyu
    """
    def __init__(self):
        super(BLANC, self).__init__()
        self.ck_set = None
        self.cr_set = None
        self.nk_set = None
        self.nr_set = None
        self.c_numerator = None
        self.n_numerator = None

    def _make_sets(self, keys: List, responses: List):
        ck_set = set()
        cr_set = set()
        nk_set = set()
        nr_set = set()
        for key in keys:
            # 对于每一组key，对其中任取两个元素进行组合
            for i in range(len(key)):
                for j in range(i+1, len(key)):
                    ck_set.add((list(key)[i], list(key)[j]))
        for response in responses:
            for i in range(len(response)):
                for j in range(i+1, len(response)):
                    cr_set.add((list(response)[i], list(response)[j]))
        for key1 in keys:
            for key2 in keys:
                if key1 == key2:
                    continue
                for k1 in key1:
                    for k2 in key2:
                        nk_set.add((k1, k2))
        for response1 in responses:
            for response2 in responses:
                if response1 == response2:
                    continue
                for r1 in response1:
                    for r2 in response2:
                        nr_set.add((r1, r2))
        self.ck_set = ck_set
        self.cr_set = cr_set
        self.nk_set = nk_set
        self.nr_set = nr_set

    def _calculate_numerator(self, kind: str):
        """
        计算分母部分，为了避免重复计算，把分母部分存为一个变量
        """
        assert kind in ['c', 'n']
        if kind == 'c':
            self.c_numerator = len(self.ck_set.intersection(self.cr_set))
        else:
            self.n_numerator = len(self.nk_set.intersection(self.nr_set))

    def _calculate_p_c(self) -> float:
        if self.c_numerator is None:
            self._calculate_numerator('c')
        return self.c_numerator / len(self.cr_set)

    def _calculate_r_c(self) -> float:
        if self.c_numerator is None:
            self._calculate_numerator('c')
        return self.c_numerator / len(self.ck_set)

    def _calculate_p_n(self) -> float:
        if self.n_numerator is None:
            self._calculate_numerator('n')
        return self.n_numerator / len(self.nr_set)

    def _calculate_r_n(self) -> float:
        if self.n_numerator is None:
            self._calculate_numerator('n')
        return self.n_numerator / len(self.nk_set)

    def calculate_f(self, keys: List, responses: List) -> float:
        if any(set_ is None for set_ in [self.cr_set, self.ck_set, self.nr_set, self.nk_set]):
            self._make_sets(keys, responses)
        pc = self._calculate_p_c()
        rc = self._calculate_r_c()
        fc = (2 * pc * rc) / (pc + rc)
        pn = self._calculate_p_n()
        rn = self._calculate_r_n()
        fn = (2 * pn * rn) / (pn + rn)
        f = (fc + fn) / 2
        self.nk_set = None
        self.nr_set = None
        self.cr_set = None
        self.ck_set = None
        self.n_numerator = None
        self.c_numerator = None
        return f

以上就是本文的全部内容，如果对你有所帮助的话，记得点赞投币加关注哦。

参考文献

[1] Scoring Coreference Partitions of Predicted Mentions: A Reference Implementation
[2] A Context-Dependent Gated Module for Incorporating Symbolic Semantics into Event Coreference Resolution