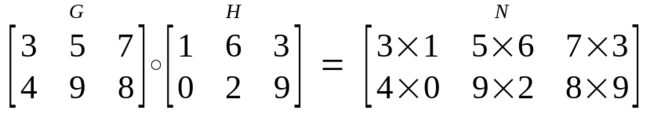【论文阅读】Time Series is a Special Sequence 1 概述与机器学习知识补充

1.概述

该模型选择了新的神经网络架构，对时间模型进行样本卷积和交互，进而选择更优的时间关系特征(temporal relation features)，应用至时间序列预测中。

架构：下采样-卷积-交互（downsample-convolve-interact architecture）

作用：扩展卷积操作的感受野(receptive field/RF)，进行多分辨率分析(multi-resolution analysis)，最终使提取的时间关系特征具有强可预测性。

2.相关知识补充

2.1感受野

在典型CNN结构中，FC层（全连接层（Fully Connected Layer），连接卷积层和普通层的普通层）每个输出节点的值都依赖FC层所有输入，而CONV层（卷积层）每个输出节点的值仅依赖CONV层输入的一个区域，这个区域之外的其他输入值都不会影响输出值，该区域就是感受野。

图中是个微型CNN，来自Inception-v3论文，原图是为了说明一个conv5x5可以用两个conv3x3代替，从下到上称为第1, 2, 3层：

1. 第2层左下角的值，是第1层左下红框中3x3区域的值经过卷积，也就是乘加运算计算出来的，即第2层左下角位置的感受野是第1层左下红框区域
2. 第3层唯一值，是第2层所有3x3区域卷积得到的，即第3层唯一位置的感受野是第2层所有3x3区域
3. 第3层唯一值，是第1层所有5x5区域经过两层卷积得到的，即第3层唯一位置的感受野是第1层所有5x5区域

就是这么简单，某一层feature map(特性图)中某个位置的特征向量，是由前面某一层固定区域的输入计算出来的，那这个区域就是这个位置的感受野。任意两个层之间都有位置—感受野对应关系，但我们更常用的是feature map层到输入图像的感受野，如目标检测中我们需要知道feature map层每个位置的特征向量对应输入图像哪个区域，以便我们在这个区域中设置anchor，检测该区域内的目标。

感受野区域之外图像区域的像素不会影响feature map层的特征向量，所以我们不太可能让CNN仅依赖某个特征向量去找到其对应输入感受野之外的目标。这里说“不太可能”而不是“绝无可能”，是因为CNN很强大，且图像像素之间有相关性，有时候感受野之外的目标是可以猜出来的，什么一叶知秋，管中窥豹，见微知著之类，对CNN目标检测都是有可能的，但猜出来的结果并不总是那么靠谱。

感受野有什么用呢？

• 一般task要求感受野越大越好，如图像分类中最后卷积层的感受野要大于输入图像，网络深度越深感受野越大性能越好
• 密集预测task要求输出像素的感受野足够的大，确保做出决策时没有忽略重要信息，一般也是越深越好
• 目标检测task中设置anchor要严格对应感受野，anchor太大或偏离感受野都会严重影响检测性能

2.1.1感受野的计算

我们首先介绍一种从后向前计算方法，极其简单适合人脑计算，看看网络结构就知道感受野了，之后介绍一种通用的从前往后计算方法，比较规律适合电脑计算，简单编程就可以计算出感受野大小和位置。

感受野是一个矩形区域，如果卷积核全都长宽相等，则对应感受野就是正方形区域。输出feature map中每个位置都对应输入图像一个感受野区域，所有位置的感受野在输入图像上以固定步进的方式平铺。

我们要计算感受野的大小r(长或宽)和不同区域之间的步进S，从前往后的方法以感受野中心(x,y)的方式确定位置，从后往前的方法以等效padding P的方式确定位置。CNN的不同卷积层，用k表示卷积核大小，s表示步进（s1表示步进是1，s2表示步进是2），下标表示层数。

从后往前的计算方式的出发点是：一个conv5x5的感受野等于堆叠两个conv3x3，反之两个堆叠的conv3x3感受野等于一个conv5x5，推广之，一个多层卷积构成的FCN感受野等于一个conv rxr，即一个卷积核很大的单层卷积，其kernelsize=r，padding=P，stride=S。

（如果我们将一个Deep ConvNet从GAP处分成两部分，看成是FCN (全卷积网络)+MLP (多层感知机)，从感受野角度看FCN等价于一个单层卷积提取特征，之后特征经MLP得到预测结果，这个单层卷积也就比Sobel复杂一点，这个MLP可能还没SVM高端，CNN是不是就没那么神秘了~）

以下是一些显(bu)而(hui)易(zheng)见(ming)的结论：

• 初始feature map层的感受野是1
• 每经过一个convkxk s1的卷积层，感受野 r = r + (k - 1)，常用k=3感受野 r = r + 2, k=5感受野r = r + 4
• 每经过一个convkxk s2的卷积层或max/avg pooling层，感受野 r = (r x 2) + (k -2)，常用卷积核k=3, s=2，感受野 r = r x 2 + 1，卷积核k=7, s=2, 感受野r = r x 2 + 5
• 每经过一个maxpool2x2 s2的max/avg pooling下采样层，感受野 r = r x 2
• 特殊情况，经过conv1x1 s1不会改变感受野，经过FC层和GAP层，感受野就是整个输入图像
• 经过多分枝的路径，按照感受野最大支路计算，shotcut也一样所以不会改变感受野
• ReLU, BN，dropout等元素级操作不会影响感受野
• 全局步进等于经过所有层的步进累乘，
• 经过的所有层所加padding都可以等效加在输入图像，等效值P，直接用卷积的输入输出公式 
• 反推出P即可

这种计算方法有多简单呢？我们来计算目标检测中最常用的两个backbone的感受野。最初版本SSD和Faster R-CNN的backbone都是VGG-16，结构特点卷积层都是conv3x3s1，下采样层都是maxpool2x2 s2。先来计算SSD中第一个feature map输出层的感受野，结构是conv4-3 backbone + conv3x3 classifier (为了写起来简单省掉了左边括号)：

r = 1 +2 +2+2+2 )x2 +2+2+2 )x2 +2+2 )x2 +2+2 = 108
S = 2x2x2 = 8
P = floor(r/2 - 0.5) = 53

以上结果表示感受野的分布方式是：在paddding=53(上下左右都加) 的输入224x224图像上，大小为108x108的正方形感受野区域以stride=8平铺。

再来计算Faster R-CNN中conv5-3+RPN的感受野，RPN的结构是一个conv3x3+两个并列conv1x1：

r = 1 +2 +2+2+2 )x2 +2+2+2 )x2 +2+2+2 )x2 +2+2 )x2 +2+2 = 228
S = 2x2x2x2 = 16
P =floor(r/2 - 0.5) = 113

分布方式为在paddding=113的输入224x224图像上，大小为228x228的正方形感受野区域以stride=16平铺。

接下来是Faster R-CNN+++和R-FCN等采用的重要backbone的ResNet，常见ResNet-50和ResNet-101，结构特点是block由conv1x1+conv3x3+conv1x1构成，下采样block中conv3x3 s2影响感受野。先计算ResNet-50在conv4-6 + RPN的感受野 (为了写起来简单堆叠卷积层合并在一起)：

r = 1 +2 +2x5 )x2+1 +2x3 )x2+1 +2x3 )x2+1 )x2+5 = 299
S = 2x2x2x2 = 16
P = floor(r/2 - 0.5) = 149

P不是整数，表示conv7x7 s2卷积有多余部分。分布方式为在paddding=149的输入224x224图像上，大小为299x299的正方形感受野区域以stride=16平铺。

ResNet-101在conv4-23 + RPN的感受野：

r = 1 +2 +2x22 )x2+1 +2x3 )x2+1 +2x3 )x2+1 )x2+5 = 843
S = 2x2x2x2 = 16
P = floor(r/2 - 0.5) = 421

分布方式为在paddding=421的输入224x224图像上，大小为843x843的正方形感受野区域以stride=16平铺。

以上结果都可以反推验证，并且与后一种方法结果一致。从以上计算可以发现一些的结论：

• 步进1的卷积层线性增加感受野，深度网络可以通过堆叠多层卷积增加感受野
• 步进2的下采样层乘性增加感受野，但受限于输入分辨率不能随意增加
• 步进1的卷积层加在网络后面位置，会比加在前面位置增加更多感受野，如stage4加卷积层比stage3的感受野增加更多
• 深度CNN的感受野往往是大于输入分辨率的，如上面ResNet-101的843比输入分辨率大3.7倍
• 深度CNN为保持分辨率每个conv都要加padding，所以等效到输入图像的padding非常大

---

前面的方法是我自用的没有出处，但后面要介绍的方法是通用的，来自一篇著名博客(需)，再次强调两种方法的结果是完全一致的：

https://medium.com/mlreview/a-guide-to-receptive-field-arithmetic-for-convolutional-neural-networks-e0f514068807​medium.com/mlreview/a-guide-to-receptive-field-arithmetic-for-convolutional-neural-networks-e0f514068807

文中给出了通用的计算公式，也是逐层计算，不同点在于这里是从前往后计算，核心四个公式：

上式中n是feature map的大小，p是padding，k是kernel size，j是jump(前面的S)，r是感受野大小，start是第一个特征向量(左上角位置)对应感受野的中心坐标位置。搬运并翻译：

• 公式一是通用计算卷积层输入输出特征图大小的标准公式
• 公式二计算输出特征图的jump，等于输入特征图的jump乘当前卷积层的步进s
• 公式三计算感受野大小，等于输入感受野加当前层的卷积影响因子(k - 1) * jin，注意这里与当前层的步进s没有关系
• 公式四计算输出特征图左上角位置第一个特征向量，对应输入图像感受野的中心位置，注意这里与padding有关系

从以上公式可以看出：start起始值为0.5，经过k=3, p=1时不变，经过k=5, p=2时不变。

博客还给出了一个计算示例：

计算出r, j和start之后，所有位置感受野的大小都是r，其他位置的感受野中心是start按照j滑窗得到。这种方法比较规律，推荐编程实现。

2.1.2有效感受野

NIPS 2016论文Understanding the Effective Receptive Field in Deep Convolutional Neural Networks提出了有效感受野（Effective Receptive Field, ERF）理论，论文发现并不是感受野内所有像素对输出向量的贡献相同，在很多情况下感受野区域内像素的影响分布是高斯，有效感受野仅占理论感受野的一部分，且高斯分布从中心到边缘快速衰减，下图第二个是训练后CNN的典型有效感受野。

这点其实也很好理解，继续回到最初那个微型CNN，我们来分析第1层，下图标出了conv3x3 s1卷积操作对每个输入值的使用次数，用蓝色数字表示，很明显越靠近感受野中心的值被使用次数越多，靠近边缘的值使用次数越少。5x5输入是特殊情况刚好符合高斯分布，3x3输入时所有值的使用次数都是1，大于5x5输入时大部分位于中心区域的值使用次数都是9，边缘衰减到1。每个卷积层都有这种规律，经过多层堆叠，总体感受野就会呈现高斯分布。

来源：卷积神经网络的感受野 - 知乎 (zhihu.com)

2.2多分辨率分析

多分辨分析(Muti-Resolution Analysis)也称多尺度分析，是S.Mallat于1989年首次提出。

多分辨率分析是信号在小波基下进行分解和重构的基本理论基础。

多分辨分析把平方可积函数x(t)∈L2(R)看成是某一逐级逼近的极限情况，每级逼近都是用某个低通平滑函数φ(t)对x(t)做平滑的结果，在逐级逼近的过程中平滑函数φ(t)也在做逐级伸缩。

其实质是：在L2的某个子空间建立基底，然后用简单的变换，把自空间上的基底扩充到L2中去。 

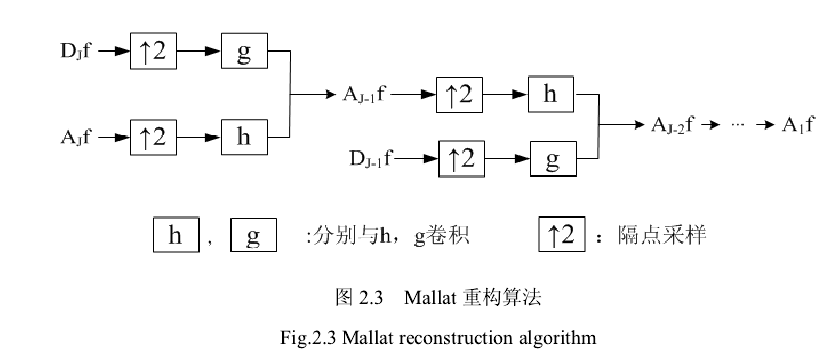
 多分辨率分析为正交小波基的构造提供了一种简单方法，同时它还是正交小波变换的快速算法(即 Mallat 算法)基本理论基础。Mallat 算法是由 S.Mallat于1989年提出的，该算法在小波分析中的作用相当于快速傅立叶变换在傅立叶分析中的作用。Mallat 算法由小波滤波器 H、G、和 h、g 对测量的信号进行分解和重构。它的分解算法可以表述为：

分解算法可以用图解的形式表示为：图 2.2

式中，h，g为时域中的小波重构滤波器，j为分解的层数，若分解的深度(分解的最高层)为J，则j=J−1,J−2,…,1,0，Aj为信号f(t)在第j层的低频部分(近似部分)的小波系数；Dj为信号f(t)在第 j 层的高频部分(细节部分)的小波系数。

来源：多分辨率分析和 MALLAT 算法 - 知乎 (zhihu.com)

3.主要工作

提出了基于时间属性的分层 TSF 框架，通过迭代提取、交换不同时间的信息分辨率，可以学习具有增强可预测性的有效表示。

通过相对较低的排列熵 (PE) 验证，构建了 SCINet 的基本构建块 SCI-Block，它将输入数据、特征下采样为两个子序列，然后使用不同的卷积滤波器提取每个子序列的特征以保留异质性信息。 为了补偿下采样过程中的信息丢失，在每个 SCI-Block 中的两个卷积特征之间加入了交互学习。

下采样

在机器学习中，得到的预测模型会趋向于预测多数集，在我们希望得到描述少数集的模型会较不准确，少数集甚至可能被当做噪声。对于不均衡数据集，为了避免少数类被忽略的情况，需要使用下采样。

常见下采样方法：随机下采样（剔除多数集中部分样本，效果不好）；EasyEnsemble（无监督学习，将多数集拆分，分别与少数集训练，最后将拆分训练得到的模型合并）和BalanceCascade（有监督学习，每轮训练不断去除正确分类的样本，对剩余样本继续训练）；NearMiss（启发式的规则来选择样本）。

时间序列预测包括单步预测、多步预测。

单步预测：

多步预测中，未来的值是基于过去的T步预测的，其中，是预测范围的长度，是在时间步t时对应的取值，d是时间序列的数。

文章中使用扩张因果卷积(Dilated Causal Convolution)进行时间序列预测。

3.1 TCN

 TCN结构由一堆因果卷积层(Causal Convolutinal Layers)、指数级增长的膨胀因子(Dilation Factor)组成。区别于普通因果卷积，只能解决大小与网络深度呈线性的时间范围的问题。TCN能够实现由较少卷积层得到较大感受野。

但由于TCN 中一个层共用一个卷积滤波器(convolutional filter)，所以限制只能从前一层的数据/特征中提取时间动态(temporal dynamics)。

TCN的一些原则：

1.输入、输出长度相等；使用 1D 全卷积网络 (FCN) 架构，每个隐藏层都有零填充。

2.不能够出现从未来泄漏到过去的情况，输出i只能跟第i层或更早的层中的元素卷积。

而TSF则不需要满足TCN的原则1.

3.2 SCINet: Sample Convolution and Interaction Network

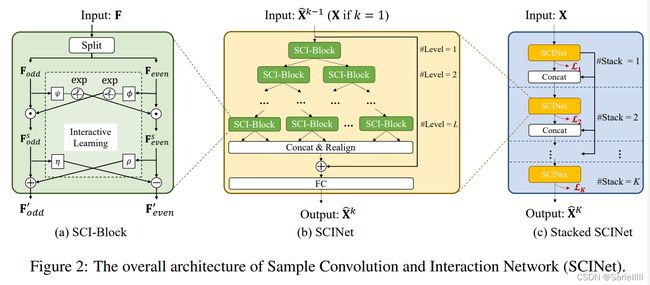
样本卷积交互网络：一个分层模型，能够通过捕捉多个位置的时间依赖性来增强原始数据的可预测性。基本框架如下：

框架层次：SCI-Block→SCINet→Stacked SCINet 

①SCI-Block将输入数据（特征）F下采样为两个子序列、，对于每组子序列选择不同卷积滤波器，以保持每个卷积的异质性性质。为了减少信息损失，在两个子序列之间使用交互学习。

②SCINet是由SCI-Block为结点构成的二叉树。在所有下采样-卷积-交互操作完成后，我们将所有低分辨率组件重新对齐并连接成一个新的序列表示， 并将其添加到原始时间序列中进行预测。

③Stacked SCINet是通过中间监督，对SCINet进行堆叠得到的，能够提取复杂的时间动态。

3.2.1 SCI-Block

SCI-Block的主要工作：使用Spliting、Interactive-learning，将输入的特征F分解为两个子特征、。

Spliting：下采样将元素分为偶元素、奇元素。、两个子集同时用于特征提取，对于每组子序列选择不同卷积层，以保持每个集合的异质性性质。

Interactive-learning：为了减少信息损失，在两个子序列之间使用交互学习。交互式学习通过相互学习仿射变换的参数来更新两个子序列，通过耦合两个互补部分的信息，可以大大增强学习到的特征的表示能力。

交互学习包括两个步骤

①使用两个不同的一维卷积模块，将、投影到隐藏状态、，转化为指数形式,将矩阵、中对应元素相乘(element-wise product)，即对两者进行放缩，其中，放缩因子是使用神经网络模块进行相互学习。

Dot product 点乘

Hadamard Product (Element -wise Multiplication， Element-wise product)

矩阵对应元素相乘

Latex指令：\bigodot

此处使用表示element-wise product

 放缩特征和被进一步投影到另外两个隐藏状态，另外两个一维卷积模块、被添加到和中或减去。最终输出更新的子特征/.

3.2.2 SCINet

SCINet是通过多个SCI-Block分层得到二叉树结构的框架。

因为随着 l 的增加，特征的时间分辨率会逐渐降低，即更深层次将包含从更浅层次传输的更精细的时间信息水平，于是可以得到 TSF 的短期和长期依赖关系。

在遍历第l级 SCI-Blocks 后，我们通过对调odd.even分裂操作，重新对子特征的元素进行排列并连接成新的序列表示，将其添加到原始时间序列中，通过残差连接(residual connection)进行预测。

Residual Connection/Skip Connect 残差连接

概述：为了解决网络层数变深后梯度消失导致训练集误差过大，允许层数低的原始信息直接传到后续的高层。

模型假设：non-linear layers可以趋近于函数H(x)，调整学习任务为residual function，即令这些层只学习残差函数，后续模块的输入是仍然是H(x)：

原理：该层网络对x求偏导的时候，多了一个常数项，所以在反向传播过程中，梯度连乘，也不会造成梯度消失。

 参考： 残差链接

最后，全连接层用于把增强的序列表示解码成，用即可表示融合后的特征/最终的预测结果。而表示的是特征/最终结果，取决于SCINet在stacked SCINet的位置。同时，该模型中的全连接层不强制要求输出长度等于输出长度（可以不同）。

相比TCN模型，SCINet优势有：不需要扩大特征提取的有效感受野，卷积操作数较少。

3.2.3 Stacked SCINet

当回溯区间的长度和预测范围的长度相近时，仅仅靠一个SCINet组件很难完成对时间依赖性的抓取，此时需要堆叠多个SCINet,形成Stacked SCINet.

特别地，为了简化中间时间特征(intermediate temporal features)，使用ground-truth对每个SCINet的输出应用中继监督(intermediate supervision)。

Deep Supervision/Intermediate Supervision(深度监督/中继监督)

在隐藏层中加了辅助的分类器，作为网络分支对主干网络进行监督。

如果直接对整个网络进行梯度下降，输出层的误差经过多层反向传播会大幅减小，即发生vanishing gradients现象。为解决此问题，在每个阶段的输出上都计算损失。这种方法可以保证底层参数正常更新。类似于GoogleNet的auxiliary classfier，用来解决网络随着深度加深而梯度消失的问题。

参考：中继监督优化(intermediate supervision)_wydbyxr的博客

第k个SCINet的输出与输入的连接，并传送到第k+1个SCINet，一般来说k都小于等于3.

3.2.4 Loss Function

用K个SCINet训练一个堆叠的SCINet，第k个中间预测的损失，计算第k个SCINet的输出与ground-truth之间的L1损失如下：

 单步预测，引入平衡参数λ∈(0,1)

多步预测， 损失为

 stacked SCINet的总损失为