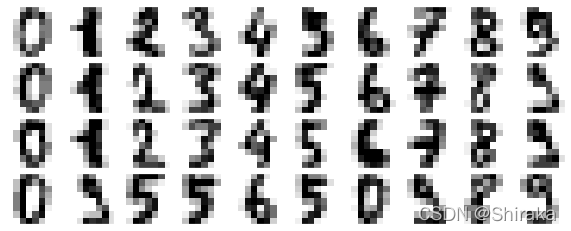主成分分析（PCA）方法步骤以及代码详解
主成分分析（PCA）方法步骤以及代码详解
前言
上一节我们了解到在构建神经网络模型，除了掌握如何搭建神经网络架构，了解参数具体含义，规避风险等方法。第一步是要对采用数据集的详细了解，无需接触任何神经网络代码，而是从彻底检查数据开始。这一步是非常关键的一步，往往我们在数据处理的某一个步骤会一定程度上的影响实验结果。本节将讲述常见的数据降维方法PCA，减少数据集的变量数量，同时保留尽可能多的信息。
1. 什么是主成分分析？
PCA（Principal Component Analysis） 是一种常见的数据分析方式，常用于高维数据的降维，可用于提取数据的主要特征分量。PCA通常用于降低大型数据集的维数，方法是数据集中的指标数量变少，并且保留原数据集中指标的大部分信息。总而言之：减少数据指标数量，保留尽可能多的信息。
1.1 PCA适用范围
- 在已标注与未标注的数据上都有降维技术
- 主要关注未标注数据上的降维技术，将技术同样也可以应用于已标注的数据。
1.2 优缺点
PCA优点在于数据降维，便于提取数据的主要特征，使得数据更容易使用，减少计算开销，去除噪音等等。缺点在于不一定需要，有可能损失有用信息，只针对训练集保留主要信息，可能造成过拟合。适用于结构化数据.PCA不仅能将数据压缩，也使得降维之后的数据特征相互独立。
2. PCA的方法步骤
PCA作为一个传统的机器学习算法，可以通过基础的线代知识推导（协方差矩阵计算，计算特征向量，特征值，正交…）。主要涉及的数学方法不在本节过多描述，有兴趣的读者可以参考花书中的线性代数部分，做推导。PCA的步骤主要分为五步；
2.1 标准化连续初始变量的范围（非结构化转成结构化）
此步骤的目的是标准化结构化指标的范围，因为PCA对于初始变量的方差非常敏感，如果初始变量的范围之间存在较大差异，则会造成很大变差，使用标准化可以将数据转换为可比较的尺度。最常用的方法主要有一下两种
- 线性函数归一化。将原始数据进行线性变换，使结果映射到[0,1]的范围，实现对原始数据的等比缩放。归一化公式如下：
X norm = X − X min X max − X min X_{\text {norm }}=\frac{X-X_{\min }}{X_{\max }-X_{\min }} Xnorm =Xmax−XminX−Xmin
- 零均值归一化。它会将原始数据映射到均值为0，标准差为1的分布上。具体来说，假设原始特征的均值μ，标准差为σ，那么归一化公式定义为：
z = x − μ σ . z=\frac{x-\mu}{\sigma} . z=σx−μ.
此方法仅限于结构化数据，对于类别型特征主要是指男，女，血型等只在有限选项内取值的特征。类别型特征原始输入通常是字符串形式，可以使用序号编码，独热编码，二进制编码等进行预处理。
-
序号编码：序号编码通常用于处理类别间具有大小关系的数据。例如成绩，可以分为 低、中、高三档，并且存在“高>中>低”的排序关系。序号编码会按照大小关系对 类别型特征赋予一个数值ID，例如高表示为3、中表示为2、低表示为1，转换后依 然保留了大小关系。
-
独热编码：独热编码通常用于处理类别间不具有大小关系的特征。例如血型，一共有4个 取值（A型血、B型血、AB型血、O型血），独热编码会把血型变成一个4维稀疏 向量，A型血表示为（1, 0, 0, 0），B型血表示为（0, 1, 0, 0），AB型表示为（0, 0, 1, 0），O型血表示为（0, 0, 0, 1）。（对于类别值较多的情况注意使用稀疏向量来节省空间，以及配合特征选择来降低维度）
-
二进制编码：二进制编码主要分为两步，先用序号编码给每个类别赋予一个类别ID，然后 将类别ID对应的二进制编码作为结果。以A、B、AB、O血型为例，表1.1是二进制 编码的过程。A型血的ID为1，二进制表示为001；B型血的ID为2，二进制表示为 010；以此类推可以得到AB型血和O型血的二进制表示。可以看出，二进制编码本 质上是利用二进制对ID进行哈希映射，最终得到0/1特征向量，且维数少于独热编 码，节省了存储空间。
-
Categorical Embedder：通过神经网络编码分类变量，有兴趣的朋友可以参考这篇文章（这个以后可能会单独列出一章讲述，不能占篇幅过大…）
对于文本类型的非结构化数据，主要使用的是词袋模型**（Bag of Words），TF-IDF，主题模型（Topic Model），词嵌入模型（Word Embedding），这个也不做过多叙述了简单叙述一下即可，对于专攻NLP**的朋友就是关公面前耍大刀了…
2.2 计算协方差矩阵以识别相关性
此步骤的目的是观察数据标签彼此是否存在相关性，观察指标间是否包含冗余信息。使用协方差矩阵是一个p * p对称矩阵（其中p是维数），它具有与所有可能的初始变量对相关联的协方差作为条目。假设三个变量x，y，z三维数据集，协方差矩阵是3 * 3矩阵如下图所示：
[ Cov ( x , x ) Cov ( x , y ) Cov ( x , z ) Cov ( y , x ) Cov ( y , y ) Cov ( y , z ) Cov ( z , x ) Cov ( z , y ) Cov ( z , z ) ] \left[\begin{array}{lll} \operatorname{Cov}(x, x) & \operatorname{Cov}(x, y) & \operatorname{Cov}(x, z) \\ \operatorname{Cov}(y, x) & \operatorname{Cov}(y, y) & \operatorname{Cov}(y, z) \\ \operatorname{Cov}(z, x) & \operatorname{Cov}(z, y) & \operatorname{Cov}(z, z) \end{array}\right] ⎣⎡Cov(x,x)Cov(y,x)Cov(z,x)Cov(x,y)Cov(y,y)Cov(z,y)Cov(x,z)Cov(y,z)Cov(z,z)⎦⎤
自身协方差是自身的方差，**（Cov(a,b)=Cov(b,a)）**是可以交换的，意味着上三角部分和下三角部分相等。如果协方差为正，则两个变量正相关，如果协方差为负，则两个变量呈负相关。
2.3 计算协方差矩阵的特征向量和特征值以识别主成分
通过计算协方差矩阵的特征向量和特征值来确定数据的主成分。首先解释一下主成分定义：主成分是由初始变量的线性组合或混合构成的新变量。新变量是互不相关的，并且初始变量中的大部分信息被挤压或压缩到第一成分中。通俗来讲，十维数据给十个主成分，PCA试图将最大可能信息放在第一个组件中，然后第二组件中放置最大的剩余信息，以此类推，直到出现下图所示内容。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mGNgYQAx-1641477720389)(…/Pictures/主成分组件.png)]
通过这种方式在主成分中组织信息，可以在不丢失太多信息的情况下降低维数生成新的指标。此时的新指标互不相关且无可解释性。它们是初始变量的线性组合。主成分表示解释最大方差量的数据的方向。方差与信息的关系是，一条携带的方差越大，沿线的数据点的离散度越高，沿线的离散度越大，它所包含的信息越多。计算协方差矩阵的特征值其实就是计算最大的方差，计算其对应的特征向量就是最佳投影方向，计算协方差矩阵特征值需要将其对角化，为了满足变化后的指标间协方差为0且指标方差尽可能大，因此要求解最大化问题，可表示为：
{ max { ω T Σ ω } s.t. ω T ω = 1 \left\{\begin{array}{l} \max \left\{\omega^{\mathrm{T}} \Sigma \omega\right\} \\ \text { s.t. } \quad \omega^{\mathrm{T}} \omega=1 \end{array}\right. {max{ωTΣω} s.t. ωTω=1
此时引用拉格朗日乘子法将问题转化为最优化问题，并对对ω求导令其等于0，便可以推出Σ ω=λ ω，此时：
D ( x ) = ω T Σ ω = λ ω T ω = λ D(\boldsymbol{x})=\boldsymbol{\omega}^{\mathrm{T}} \Sigma \boldsymbol{\omega}=\lambda \boldsymbol{\omega}^{\mathrm{T}} \boldsymbol{\omega}=\lambda D(x)=ωTΣω=λωTω=λ
将计算好的特征值的顺序对特征向量进行排序，从高到低，可以按照重要程度顺序获得主成分。
2.4 创建特征向量来决定保留那些主成分
计算特征向量并按照特征值降序对他们进行排序，使我们可以按照重要性顺序找到主成分。在这一步骤我们选择保留所有特征值还是丢弃那些重要程度较低的特征值。并与剩余的特征值形成一个成为特征向量的向量矩阵。特征向量只是一个矩阵，列为我们决定保留的特征向量。此步骤根据我们的需求来决定。通常是取特征值前d对应的特征向量量ω1 ,ω2 ,…,ωd，通过以下映射将n维样本映射到d维；
x i ′ = [ ω 1 T x i ω 2 T x i ⋮ ω d T x i ] \boldsymbol{x}_{i}^{\prime}=\left[\begin{array}{c} \boldsymbol{\omega}_{1}^{\mathrm{T}} \boldsymbol{x}_{i} \\ \boldsymbol{\omega}_{2}^{\mathrm{T}} \boldsymbol{x}_{i} \\ \vdots \\ \boldsymbol{\omega}_{d}{ }^{\mathrm{T}} \boldsymbol{x}_{i} \end{array}\right] xi′=⎣⎢⎢⎢⎡ω1Txiω2Txi⋮ωdTxi⎦⎥⎥⎥⎤
新的xi ′的第d维就是xi在第d个主成分ωd方向上的投影，通过选取最大的d个特 征值对应的特征向量，我们将方差较小的特征（噪声）抛弃，使得每个n维列向量 xi被映射为d维列向量xi ′，定义降维后的信息占比为；
η = ∑ i = 1 d λ i 2 ∑ i = 1 n λ i 2 \eta=\sqrt{\frac{\sum_{i=1}^{d} \lambda_{i}{ }^{2}}{\sum_{i=1}^{n} \lambda_{i}{ }^{2}}} η=∑i=1nλi2∑i=1dλi2
2.5 沿主成分轴重铸数据
在这一步骤，使用协方差矩阵的特征向量形成的特征值，将数据从原始轴重新定向到主成分表示的轴。可以将原始数据集的转置乘以特征向量的转置来完成。
2.6 总结
除了使用目标函数求解最大方差外，可以考虑其他思路分析，例如最小回归误差得到新的目标函数。实际上对应原理和求解方法与该方法是等价的。PCA是一种线性降维方法，具有一定的局限性，可以考虑通过核映射对PCA机械能扩展得到核主成分分析（KPCA），可以通过流形映射降维方法，比如等距映射，局部线性嵌入，拉普拉斯特征映射等，对一些PCA效果不好的复杂数据集进行非线性降维操作。
下面将会举例使用PCA降维处理
3 深入PCA
到目前为止，我们研究了PCA的理论基础，PCA从根本上来说是降维算法，但它也可以用作可视化，噪声过滤，特征提取和工程等工具。下面根据scikit-learn库来进一步展示如何应用
3.1 PCA应用于可视化部分
3.11 代码实现——理论部分
- 导入相关库
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
- 主成分分析作为一种快速灵活的无监督数据降维方法。它的可视化相对简单。随机生成200点
rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal');
结果如下图所示：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lWuUaxiD-1641477720391)(…/Pictures/PCA可视化图.png)]
- 很显然，x与y变量之间存在近乎线性的关系。与线性回归的问题不同，PCA是试图了解x与y变量之间的关系。在PCA中，通过scikit-learn库的PCA估计器可以计算数据中的主轴列表并使用这些轴来表述数据集来量化这种关系。
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
print(pca.components_)
print(pca.explained_variance_)
PCA分量；
PCA解释方差；
通过拟合从数据中学习一些信息，最重要的是分量和解释方差，对于这些数字的概念，让我们将其可视化为输入数据上的向量，使用分量来定义向量的方向，使用解释方差来定义向量的平方长度。
def draw_vector(v0, v1, ax=None):
ax = ax or plt.gca()
arrowprops=dict(arrowstyle='->',
linewidth=2,
shrinkA=0, shrinkB=0)
ax.annotate('', v1, v0, arrowprops=arrowprops)
# plot data
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal');
将数据投影，这些向量代表数据的主轴，向量的长度表明该轴在描述数据分布方面的重要性，更准确的说，它是投影时数据方差的度量到那个轴。每个数据点在主轴上的投影是数据的主成分。这种从数据轴到主轴的变换被称为affine transformation，基本上由平移，旋转和均匀缩放组成（有这一定意义的应用）。
3.1.2 可视化PCA案例：手写数字
降维的用处在二维表示并不明显，在查看高维数据时会变得更加清晰。通过手写数字数据集展示PCA对数据的应用
首先加载数据：
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
digits = load_digits()
digits.data.shape
整个数据的维度是由8*8像素组成，一共64维。我们可以通过PCA将它们投影到更易于使用的维度数量：
#将数据投影到2维（可以自主决定投影维度）
pca = PCA(2) # project from 64 to 2 dimensions
projected = pca.fit_transform(digits.data)
print(digits.data.shape)
print(projected.shape)
可视化每个点的前两个主成分以了解数据：
plt.scatter(projected[:, 0], projected[:, 1],
c=digits.target, edgecolor='none', alpha=0.5,
cmap=plt.cm.get_cmap('Accent', 10))
plt.xlabel('component 1')
plt.ylabel('component 2')
plt.colorbar();
完整的数据是64维度的点云，这些点是每个数据点沿着方差最大的方向的投影。本质上，我们已经找到了64维空间中的最佳拉伸和旋转，使我们能够在二维空间中看到数字布局（不参考标签）。
3.1.3 关于component的定义
这个含义可以从基向量的组合的角度来理解。比如训练集中的每幅图像都由64个像素值集合定义，我们将其称之为向量x：
x = [ X 1 , X 2 , X 3 ⋯ X 64 ] x=\left[X_{1}, X_{2}, X_{3} \cdots X_{64}\right] x=[X1,X2,X3⋯X64]
为了构建图像，我们将向量的每个元素乘以它所描述的像素，然后将结果相加以构建图像：
image ( x ) = x 1 ⋅ ( pixel 1 ) + x 2 ⋅ ( pixel 2 ) + x 3 ⋅ ( pixel 3 ) ⋯ x 64 ⋅ ( pixel 64 ) \begin{array}{c} \operatorname{image}(x)=x_{1} \cdot(\text { pixel } 1)+x_{2} \cdot(\text { pixel } 2)+x_{3} \cdot(\text { pixel } 3) \cdots x_{64} \\ \cdot(\text { pixel } 64) \end{array} image(x)=x1⋅( pixel 1)+x2⋅( pixel 2)+x3⋅( pixel 3)⋯x64⋅( pixel 64)
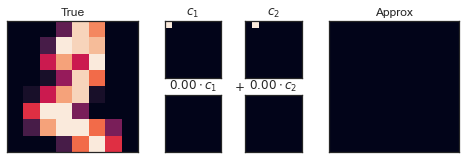
此时可以想象减少这些数据的维度的一种方法是将这些基向量中的一部分归零。例如，如果我们只是用前两个像素，我们将会得到二维投影，但它不能很好地反映整个图像，我们已经扔掉了大部分的像素。
def plot_pca_components(x, coefficients=None, mean=0, components=None,
imshape=(8, 8), n_components=2, fontsize=12,
show_mean=True):
if coefficients is None:
coefficients = x
if components is None:
components = np.eye(len(coefficients), len(x))
mean = np.zeros_like(x) + mean
fig = plt.figure(figsize=(1.2 * (5 + n_components), 1.2 * 2))
g = plt.GridSpec(2, 4 + bool(show_mean) + n_components, hspace=0.3)
def show(i, j, x, title=None):
ax = fig.add_subplot(g[i, j], xticks=[], yticks=[])
ax.imshow(x.reshape(imshape), interpolation='nearest')
if title:
ax.set_title(title, fontsize=fontsize)
show(slice(2), slice(2), x, "True")
approx = mean.copy()
counter = 2
if show_mean:
show(0, 2, np.zeros_like(x) + mean, r'$\mu$')
show(1, 2, approx, r'$1 \cdot \mu$')
counter += 1
for i in range(n_components):
approx = approx + coefficients[i] * components[i]
show(0, i + counter, components[i], r'$c_{0}$'.format(i + 1))
show(1, i + counter, approx,
r"${0:.2f} \cdot c_{1}$".format(coefficients[i], i + 1))
if show_mean or i > 0:
plt.gca().text(0, 1.05, '$+$', ha='right', va='bottom',
transform=plt.gca().transAxes, fontsize=fontsize)
show(slice(2), slice(-2, None), approx, "Approx")
return fig
from sklearn.datasets import load_digits
digits = load_digits()
sns.set_style('white')
fig = plot_pca_components(digits.data[2],
show_mean=False)
可视化上排图片表示单个像素，下排显示这些像素对图像构建的累计贡献。仅仅使用两个基于像素的组件是明显不够的，只能构建64像素图像的很小一部分。像素表示法并不是唯一的基础选择，我们也可以使用其他的基函数，这些基函数包含了每个像素的一些预定义的贡献。
image ( x ) = mean + x 1 ⋅ ( basis 1 ) + x 2 ⋅ ( basis 2 ) + x 3 ⋅ ( basis 3 ) ⋯ \text { image }(x)=\operatorname{mean}+x_{1} \cdot(\text { basis } 1)+x_{2} \cdot(\text { basis } 2)+x_{3} \cdot(\text { basis } 3) \cdots image (x)=mean+x1⋅( basis 1)+x2⋅( basis 2)+x3⋅( basis 3)⋯
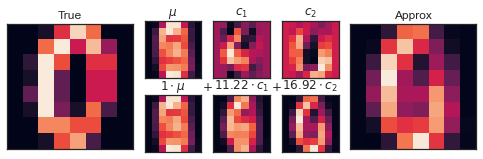
PCA可以被认定为选择最佳基函数的过程，这样只需要将前几个相加就足以重建数据集中的大部分元素。作为数据中的低维表示的主成分只是将这个系列的每个元素相乘的系数。下图显示了使用平均值加上前两个PCA基函数重建该数字的相应描述：
pca = PCA(n_components=2)
Xproj = pca.fit_transform(digits.data)
sns.set_style('white')
fig = plot_pca_components(digits.data[10], Xproj[10],
pca.mean_, pca.components_)
可视化如下图所示：
与像素基础不同，PCA允许使用均值加上两个分量来恢复输入图像的显著特征。每个分量中的每个像素数量是我们二维展示中向量方向的推论。PCA组成了一组比原始数据更简单有效的函数。那么如何选择组件的数量使得整个函数达到最优呢
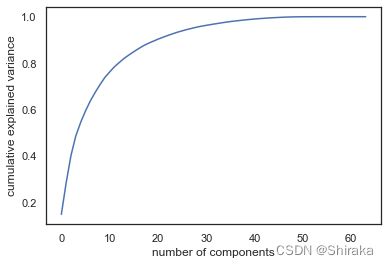
3.1.4 如何确定组件的数量
如何选择组件的数量来描述数据，可以通过观察成分数量的函数的累计解释方差率来确定。
pca = PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
可视化结果如下：
这条曲线量化了64维方差中有多少包含在第N组件的，例如，我们可以看到前十个分量包含大约**75%的方差，需要50个分量描述99%**的方差。通过可视化可以帮助我们了解冗余级别。
3.2 PCA应用于噪声过滤
3.2.1 代码实现——理论部分
PCA可应用与噪声过滤。理论在于：任何方差比噪声影响大的分量相对不收噪声影响。说人话就是仅使用最大的主成分子集重建数据，优先保留信号排除噪声。
首先观察数字数据之间的关系。
def plot_digits(data):
fig, axes = plt.subplots(4, 10, figsize=(10, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8, 8),
cmap='binary', interpolation='nearest',
clim=(0, 16))
plot_digits(digits.data)
添加一些随机噪声，创建数据集，重新绘制。
np.random.seed(42)
noisy = np.random.normal(digits.data, 4)
plot_digits(noisy)
现在数据集为含噪声的手写识别，包含虚假像素，我们很难用肉眼识别数字。让我们在这个数据集上训练PCA，要求投影保留50%方差。
pca = PCA(0.50).fit(noisy)
pca.n_components_
运行结果为12，50%的防擦好相当于12个主成分。现在我们计算这些分量，然后使用变换来重建过滤后的数字：
components = pca.transform(noisy)
filtered = pca.inverse_transform(components)
plot_digits(filtered)
可视化图像可以明显发现，PCA具有噪声过滤的特点，通过PCA降维的数据具有特征选择的功能。
3.2.2PCA应用于降维——野外标记人脸（参考scikit-learn官方案例）
- 项目概述
Labeled Faces in the Wild是人脸验证的公共基准，样本包含1850个特征，我们使用PCA来观察能否对这些特征进行降维处理；
-
开发流程
- 下载数据：观察数据集中标签和样本
- 下载数据：观察数据集中标签和样本
2) 观察样本标签内容：
-
准备数据，观察数据特征，计算合适组件数量：
from sklearn.datasets import fetch_lfw_people from sklearn.decomposition import PCA as RandomizedPCA faces = fetch_lfw_people(min_faces_per_person=60) print(faces.target_names) print(faces.images.shape) pca = RandomizedPCA(150) pca.fit(faces.data)
总样本为1288个，样本特征为1850（忽略第一步数据清洗部分）适合组件为150
4.
```python
fig, axes = plt.subplots(3, 8, figsize=(9, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(pca.components_[i].reshape(62, 47), cmap='bone')
```
绘制组件曲线图：
```
import numpy as np
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
```
计算组件重构图像，并可视化结果：
在这种高维数据情况下，可视化与前几个主成分相关联的图像，可以观察其图像变化情况（不知道为什么官方称呼为eigenfaces很奇怪的名字）。我们可以看到150分量占方差95%以上。我们可可以使用150个组件重构数据的大部分特征，将输入图像与重构图像进行比较如下图所示；
```
# Compute the components and projected faces
pca = RandomizedPCA(150).fit(faces.data)
components = pca.transform(faces.data)
projected = pca.inverse_transform(components)
# Plot the results
fig, ax = plt.subplots(2, 10, figsize=(10, 2.5),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i in range(10):
ax[0, i].imshow(faces.data[i].reshape(62, 47), cmap='binary_r')
ax[1, i].imshow(projected[i].reshape(62, 47), cmap='binary_r')
第一行显示输入图像，第二行显示从三千个初始特征中150个组件重构图像。尽管数据的维度减少近20倍，我们仍然可以用肉眼可判断重构图像的信息。意味着我们的分类算法足够有效，更有利于分类。
4 拓展
本节，我们从理论推导到代码分析，到案例分析，充分的讨论了PCA有关的知识，如何进行降维，高纬度可视化，噪声过滤，特征选择，相信大家一定和我一样收获满满。对于降维处理方法，除此之外PCA也存在一些使用限制，例如高阶相关性，需要通过一些函数将非线性转化为线性相关，在进行降维。在无监督降维问题中还有随机投影，特征聚集等方法减少数据维度，有兴趣的朋友可以参考scikit-learn官方教程。
参考文献
- 《百面机器学习》
- aces recognition example using eigenfaces and SVMs
- A Step-by-Step Explanation of Principal Component Analysis (PCA)
- 利用PCA来简化数据
- In Depth: Principal Component Analysis
推荐阅读
- 微分算子法
- 使用PyTorch构建神经网络模型进行手写识别
- 使用PyTorch构建神经网络模型以及反向传播计算
- 如何优化模型参数，集成模型
- TORCHVISION目标检测微调教程