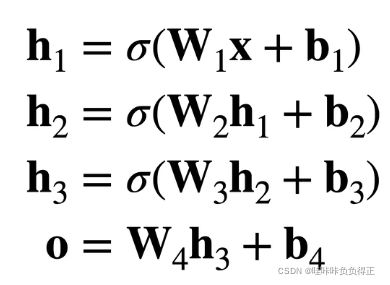Pytorch 多层感知机

多层感知机

0. 环境介绍

环境使用 Kaggle 里免费建立的 Notebook

教程使用李沐老师的 动手学深度学习 网站和 视频讲解

小技巧：当遇到函数看不懂的时候可以按 Shift+Tab 查看函数详解。

1. 多层感知机概述

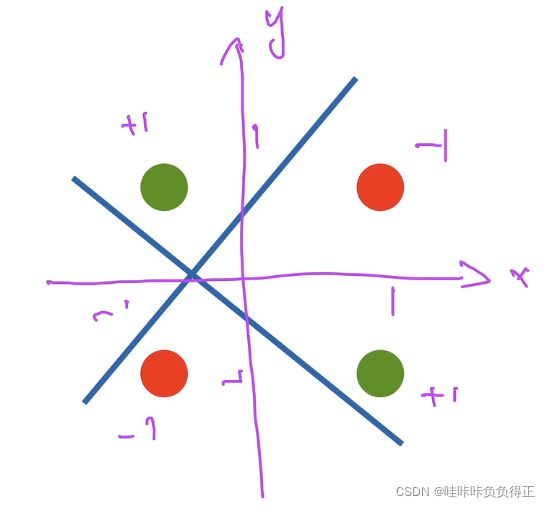
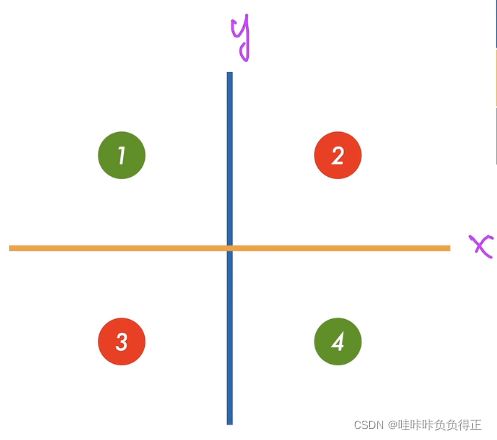
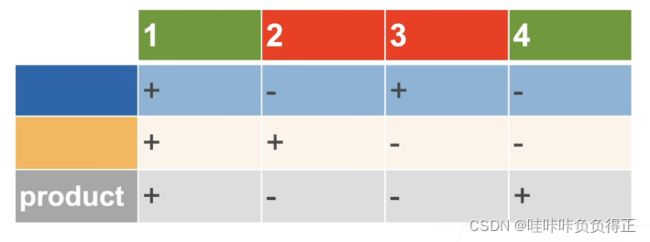
1.0 感知机

感知机是一个二分类模型。
感知机训练过程：

感知机模型不能拟合 XOR 函数，它只能产生线性分割面。

1.1 多层感知机

1.1.1 学习 XOR

学习两条线：

得到结果：

结构示意图：

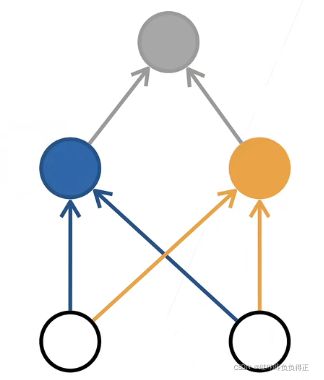
1.1.2 隐藏层

在网络中加入一个或多个隐藏层来克服线性模型的限制， 使其能处理更普遍的函数关系类型。 每一层都输出到上面的层，直到生成最后的输出。 我们可以把前 $L-1$ 层看作表示，把最后一层看作线性预测器。

单隐藏层单分类：

单隐藏层多分类：

多隐藏层：

1.1.3 MLP 结构

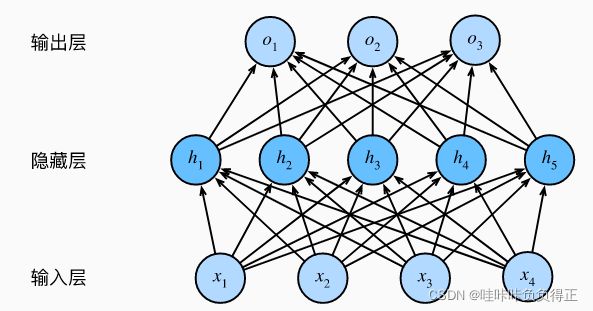
怎么设计网络比较好？
李沐老师说：更深且瘦的网络效果可能要比浅而胖的网络效果要好，浅而胖的网络容易过拟合。但是老师也说这个没有理论依据，但效果上确实要好。

1.1.4 激活函数

激活函数（activation function）通过计算加权和并加上偏置来确定神经元是否应该被激活， 它们将输入信号转换为输出的可微运算。

并且激活函数必须是非线性的。若激活函数是线性的话，即使经过多层感知机，运算结果还是 $W_{ij}$ 的线性组合，即还是线性的，无法解决非线性问题。

为方便理解：
浙江大学 胡浩基老师的机器学习课程 6:50 左右有例子。

1.1.4.1 ReLU

最受欢迎的激活函数是修正线性单元（Rectified linear unit，ReLU）， 因为它实现简单，同时在各种预测任务中表现良好。 ReLU 提供了一种非常简单的非线性变换。

ReLU 激活函数公式：
$$\mathrm{ReLU}(x)=\max (x,0)$$

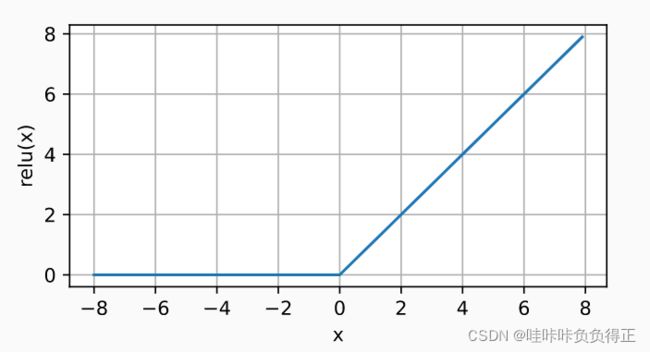
使用ReLU的原因是，它求导表现得特别好：要么让参数消失，要么让参数通过。 这使得优化表现得更好，并且ReLU减轻了困扰以往神经网络的梯度消失问题。

1.1.4.2 Sigmoid

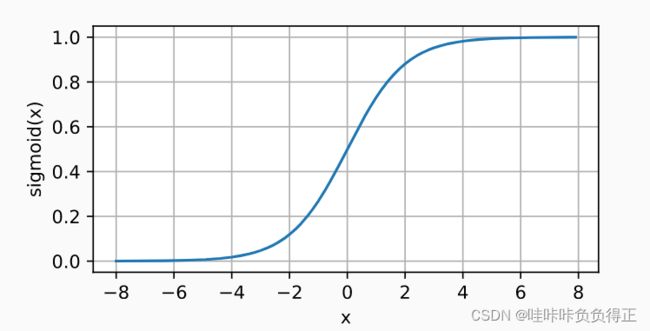
将输入投影到 $(0,1)$。
Sigmoid激活函数的公式：
$$\mathrm{sigmoid}(x)=\frac{1}{1+\exp (-x)}.$$

1.1.4.3 tanh

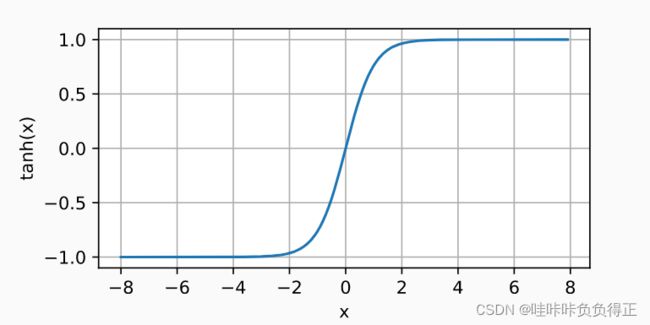
与 sigmoid 函数类似， tanh (双曲正切)函数能将其输入压缩转换到区间 $(-1,1)$ 上。
tanh 激活函数的公式：
$$\tanh (x)=\frac{1-\exp (-2x)}{1+\exp (-2x)}.$$

1.1.5 超参数

• 隐藏层数
• 每层隐藏层的大小（神经元个数）

2. 从零实现

2.0 导入模块

!pip install -U d2l # install d2l 模块
import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

2.1 初始化模型参数

实现一个具有单隐藏层的多层感知机， 它包含 $256$ 个隐藏单元。

通常，我们选择 $2$ 的若干次幂作为层的宽度。 因为内存在硬件中的分配和寻址方式，这么做往往可以在计算上更高效。

num_inputs, num_outputs, num_hiddens = 784, 10, 256
# 第一层
W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
# 第二层
W2 = nn.Parameter(torch.randn(
    num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

2.2 激活函数（ReLU）

def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)

2.3 模型

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X@W1 + b1)  # 这里“@”代表矩阵乘法
    return (H@W2 + b2)

2.4 损失函数

loss = nn.CrossEntropyLoss(reduction='none')

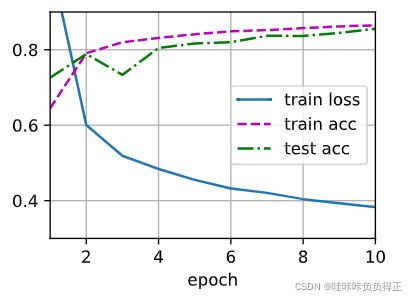
2.5 训练

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

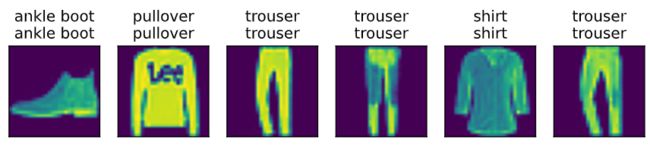
2.6 预测

d2l.predict_ch3(net, test_iter)

3. 简洁实现

3.0 导入模块

import torch
from torch import nn
from d2l import torch as d2l

3.1 模型

net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

3.2 损失函数，优化器

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)

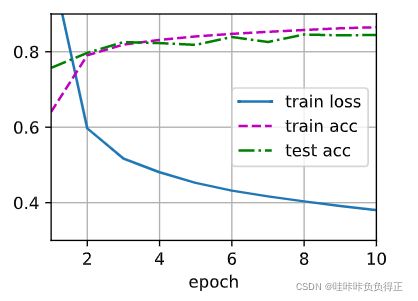
3.3 训练

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)